Página de estudos de matemática e sequências numéricas

Triângulo Numérico 3 - números quadrados, retangulares e primos gêmeos - 395

Triângulo numérico é um dispositivo no qual números são dispostos sequencialmente linha a linha formando figura geométrica de triângulo, podendo ser em formato de um triângulo retângulo, triângulo isóceles ou um triângulo equilátero.

Interessante pontuar que triângulos possuem diversas propriedades matemáticas relacionadas às suas formas, lados e ângulos com as quais são possíveis de se realizarem variados cálculos para se saber por exemplo: altura de um edifício, comprimento da sombra de uma árvore, distância de um objeto, etc.

Dispondo números sequencialmente em formato de um triângulo, obtêm-se outras propriedades e outras sequências numéricas que se relacionam entre si como também com outras sequências numéricas, exemplo clássico é o extraordinário Triângulo de Pascal, também conhecido como Triângulo de Tartaglia, Triângulo de Yang Hui ou simplesmente Triângulo Aritmético ou Triângulo Numérico que a partir do número 1 formando dois lados de um triângulo são possíveis de se obterem diversas relações matemáticas entre sequências numéricas famosas.

Triângulo Numérico 3 e sua construção

O Triângulo Numérico 3, assim é denominado, pois se assemelha a triângulos publicados no livro digital Números Triangulares e Sequências Numéricas, apresentando interessantes relações numéricas nas quais são possíveis se obterem números primos gêmeos.

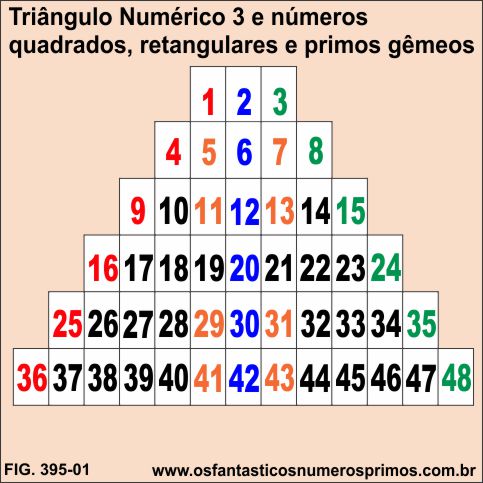
O Triângulo Númerico 3 é construído a partir das seguintes etapas:

1) na 1^a linha, colocam-se 3 números começando com o número quadrado perfeito 1 até um número antecessor do próximo número quadrado perfeito 4: 1, 2, 3;

2) na 2^a linha, colocam-se 5 números começando com o número quadrado perfeito 4 até um número antecessor do próximo número quadrado perfeito 9: 4, 5, 6, 7, 8;

3) na 3^a linha, colocam-se 7 números começando com o número quadrado perfeito 9 até um número antecessor do próximo número quadrado perfeito 16: 9, 10, 11, 12, 13, 14, 15;

E assim para as demais linhas, sempre começando com um número quadrado perfeito e terminando com um número antecessor de um número quadrado perfeito.

Cada linha é constituída por quantidade de termos ímpares.

Triângulo Numérico 3 e propriedades

O Triângulo Numérico 3 possui interessantes propriedades numéricas, vejamos algumas delas:

Fonte: SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

Números quadrados perfeitos

O lado esquerdo do Triângulo Numérico 3 é constituído por números quadrados perfeitos (cor vermelha).

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ...

Número quadrado perfeito somado com sua raiz quadrada tem como resultado um número retangular que se encontra na altura do Triângulo Numérico 3.

Exemplos:

1 + 1 = 2

4 + 2 = 6

9 + 3 = 12

Número quadrado perfeito somado com o dobro da sua raiz quadrada tem como resultado um número que se encontra no final da linha do Triângulo Numérico 3.

Exemplos:

1 + (2 x 1) = 3

4 + (2 x 2) = 8

9 + (2 x 3) = 15

Números quase quadrados perfeitos

Números quase quadrados perfeitos são números de 1 unidade menor que números quadrados perfeitos.

3, 8, 15, 24, 35, 48, 63, 80, 99,...

Os números quase quadrados perfeitos (cor verde) se encontram nos finais de cada uma das linhas do Triângulo Numérico 3.

Números retangulares / oblongos

A altura do Triângulo Numérico 3 é constituída por números retangulares, também denominados de números oblongos (cor azul).

2, 6, 12, 20, 30, 42, 56, 72,...

Números retangulares / oblongos são números figurados, isto é, por meio de arranjos de pontos podemos representar figuras geométricas.

Um dos métodos de se obterem números retangulares é multiplicar dois números consecutivos.

Exemplos:

1 x 2 = 2

2 x 3 = 6

3 x 4 = 12

Termos equidistantes

A soma de dois termos equidistantes numa linha e posteriormente dividida por 2 tem como quociente um número retangular que se encontra na altura do Triângulo Numérico 3.

Exemplos:

primeira linha

a) (1 + 3) / 2 = 2

segunda linha

a) (4 + 8) / 2 = 6

b) (5 + 7) / 2 = 6

Números quadrados e números quase-quadrados perfeitos

O Triângulo Numérico 3 apresenta relações numéricas entre números quadrados perfeitos e números quase-quadrados perfeitos e números perfeitos.

A média aritmética entre um número quadrado perfeito e um número quase-quadrado perfeito tem como quociente um número retangular.

A metade de um número retangular é um triangular.

Entre os números triangulares estão os números perfeitos.

Os números quadrados perfeitos e os números quase quadrados perfeitos se encontram em cada lado do Triângulo Númerico 3.

primeira linha

( 1 + 3 ) / 2 = 2

segunda linha

(4 + 8) / 2 = 6

terceira linha

( 9 + 15 ) / 2 = 12 (número retangular)

12 : 2 = 6 (número perfeito)

3 é a ordem / posição do número triangular e perfeito 6

3 é a soma de potências de base 2

1 + 2 = 3

Se a soma consecutiva de potências de base 2 tiver como resultado um número primo e este multiplicado pelo último termo da sequência, então o produto é um número perfeito.

3 x 2 = 6 (número perfeito)

Fórmula de Euclides para números perfeitos

para n = 2:

2^2-1 x (2² − 1)

2 x 3 = 6 (número perfeito)

Números primos gêmeos

Números primos gêmeos são duplas de números primos cuja diferença entre eles são 2 unidades (cor laranja).

Determinados números retangulares / oblongos são as médias aritméticas de números primos gêmeos.

Exemplos:

segunda linha

5 e 7 são primos gêmeos

(5 + 7) / 2 = 6

terceira linha

11 e 13 são primos gêmeos

(11 + 13) / 2 = 12

quinta linha

29 e 31 são primos gêmeos

(29 + 31) / 2 = 30

Soma das linhas

Cada linha do Triângulo Numérico 3 forma uma progressão aritmética finita de quantidades ímpares de termos.

A soma dos termos de cada linha do Triângulo Numérico 3 tem como resultado um número divisivel pelo número retangular correspondente a essa linha.

Exemplos:

primeira linha

6 : 2 = 3 (quantidade de termos na primeira linha)

O dobro da raiz quadrada mais 1 multiplicado pelo quadrado mais a sua raiz quadrada tem como resultado a soma da linha.

[ (2 x √1) + 1 ] x [ 1² + √1] =

3 x 2 = 6

segunda linha

30 : 6 = 5 (quantidade de termos na segunda linha)

O dobro da raiz quadrada mais 1 multiplicado pelo quadrado mais a sua raiz quadrada tem como resultado a soma da linha.

[ (2 x √4) + 1 ] x [ 2² + √4] =

5 x 6 = 30

terceira linha

84 : 12 = 7 (quantidade de termos na terceira linha)

O dobro da raiz quadrada mais 1 multiplicado pelo quadrado mais a sua raiz quadrada tem como resultado a soma da linha.

[ (2 x √9) + 1 ] x [ 3² + √9] =

7 x 12 = 84

Média aritmética

A média aritmética de cada uma das linhas do Triângulo Numérico 3 tem como resultado o número retangular que se encontra na altura do triângulo e nessa mesma linha.

Exemplos:

primeira linha

(1 + 2 + 3) : 3 = 2

segunda linha

(4 + 5 + 6 + 7 + 8) : 5 = 6

Novos métodos e fórmulas

Os novos métodos e fórmulas que se seguem foram desenvolvidos pelo Sr. David Dias Marques, Entusiasta Matemático, residente na Cidade de Paracuru-CE, vejamos:

Exemplo com a segunda linha do Triângulo Numérico 3.

A segunda linha do Triângulo Numérico 3 é formada por uma progressão aritmética de 5 termos:

a1 = 4

É o primeiro termo da sequência e é um número quadrado perfeito.

Fórmula 1

O dobro da raiz quadrada do primeiro termo (a1) tem como resultado a quantidade de termos depois do termo (a1), isto é, após um número quadrado perfeito.

2 √4 =

2 x 2 = 4

Após o número quadrado perfeito 4, tem-se 4 termos: 5, 6, 7, 8.

Fórmula 2

A soma do termo a1 e 1 unidade tem como resultado um número irracional.

4 + 1 = 5

√5 = 2,2360679774997896964091736687313...

Número Irracional é um número cuja a representação decimal é infinita e não periódica. Não há um mesmo padrão que se repete após a vírgula.

Fórmula 3

A soma do termo a1 com a raiz quadrada do termo a1 tem como resultado o termo central da sequência numérica.

4 + √4 =

= 4 + 2

= 6

4, 5, 6, 7, 8

6 é o termo central (termo médio) da sequência numérica.

Fórmula 4

O dobro da raiz quadrada do primeiro termo (a1) e 1 unidade tem como resultado a quantidade de termos da sequência numérica numérica.

2 √4 + 1 =

2 x 2 + 1 = 5

4, 5, 6, 7, 8 é uma sequência númerica constituída por 5 termos.

Fórmula 5

A soma do primeiro termo (a1) com o dobro da raiz quadrada do primeiro termo (a1) tem como resultado o último termo da sequência numérica.

4 + 2 √4 =

4 + 4 = 8

4, 5, 6, 7, 8

8 é o último termo da sequência numérica.

Fórmula 6 (nova fórmula)

O dobro da raiz quadrada do termo (a1) somado 1 unidade e multiplicado pelo quadrado somado com a sua raiz quadrada tem como resultado a soma dos termos da sequência numérica.

[ (2 x √4) + 1 ] x [ 4 + √4] =

5 x 6 = 30

Números Quadrados Perfeitos terminados em 5

Números Quadrados Perfeitos terminados em 5 originados de múltiplos de 5 terminados em 5 são formados por números cujos dois algarismos finais é o número 25 e os algarismos iniciais formados por números retangulares.

Número retangular dividido por 2 tem como resultado um número triangular.

Para mais informações, veja:

011-estudos-549-numeros-retangulares-numeros-quadrados-perfeitos-terminados-em-cinco

Autor: Ricardo Silva - agosto/2022

atualizado em janeiro/2025

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-291-numeros-retangulares-sequencias-numericas

011-estudos-335-numeros-quadrados-perfeitos-e-numeros-retangulares

011-estudos-336-numeros-retangulares-e-numeros-primos-gemeos

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.