


Segmento Áureo, Proporção Áurea, Razão Dourada, são denominações originadas da divisão de um segmento de reta em média e extrema razão e que está publicado no livro VI de Os Elementos de Euclides de Alenxandria.
Dividindo-se um termo por um termo anterior da Sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34,... obtem-se o Número Phi (Ф), também conhecido como Número de Ouro, Razão Áurea, Razão Dourada que é o número irracional 1,618033657...
Triângulo Retângulo Pitagórico é um triângulo cujos lados são formados por números inteiros e que satisfazem ao Teorema de Pitágoras: a2 = b2 + c2, O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
O estudo demonstra que há sempre Triângulo Retângulo subjacente nas construções geométricas da divisão de segmento em média e extrema na menor parte da divisão de um seguimento de reta nas figuras geométricas de um triângulo retângulo de razão 1:2 e do quadrado que tende para um Triângulo Retângulo Pitagórico com medidas de ângulos agudos aproximados de 37 e 53 graus.
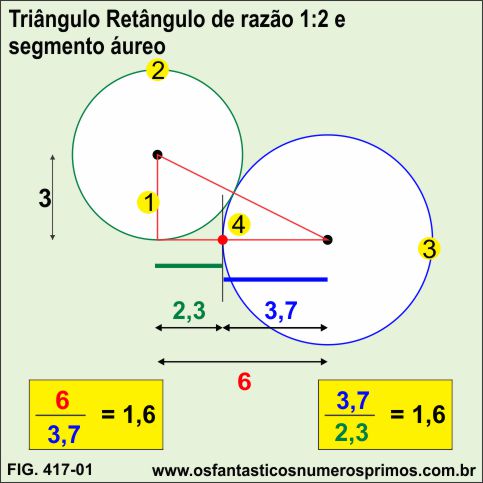
A partir de um triângulo retângulo de razão 1:2, isto é, base o dobro da altura ou altura o dobro da base, e seguindo as etapas de 1 a 4, determina-se seguimento em média e extrema razão (segmento áureo).
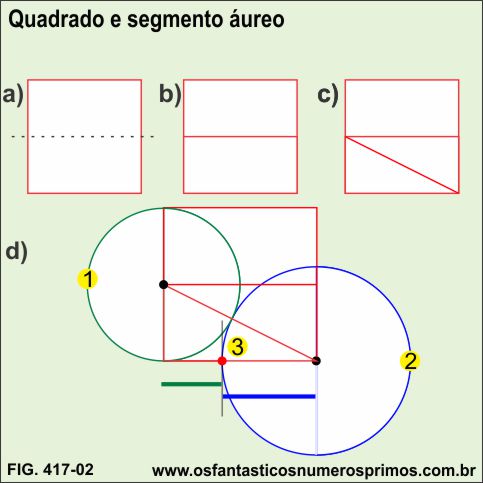
Dividindo-se um quadrado em duas partes, obtêm-se dois retângulos de razões 1:2.
A partir do retângulo da base e trançando-se uma diagonal, geram-se dois triângulos retângulos de razões 1:2.
Escolhe-se o triângulo retângulo da base do quadrado e determina-se o seguimento em média e extrema razão (razão áurea) conforme etapas a de 1 a 3.
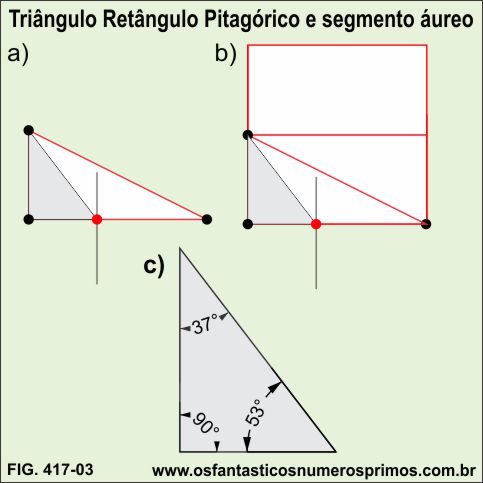
Determinado o ponto de divisão em média e extrema razão a partir da base de um triângulo retângulo de razão 1:2 ou triângulo retângulo gerado do quadrado e unindo-os vértices do lado do cateto menor e o ponto de divisão em média e extrema razão, forma-se um Triângulo Retângulo cujos ângulos agudos são aproximadamente 37 e 53 graus e que são ângulos agudos de um Triângulo Retângulo Pitagórico 3-4-5.
Os 6 primeiros ternos da Sequência de Fibonacci são: 1, 1, 2, 3, 5, 8,...
Construindo-se um quadrado de lado 8 (Número de Fibonacci), dividindo-o ao meio e determinando a divisão em média e extrema razão, a partir do ponto áureo, o triângulo formado (cor azul) é um Triângulo Retângulo cujos ângulos agudos são aproximadamente 37 e 53 graus e que são ângulos agudos de um Triângulo Retângulo Pitagórico 3-4-5.
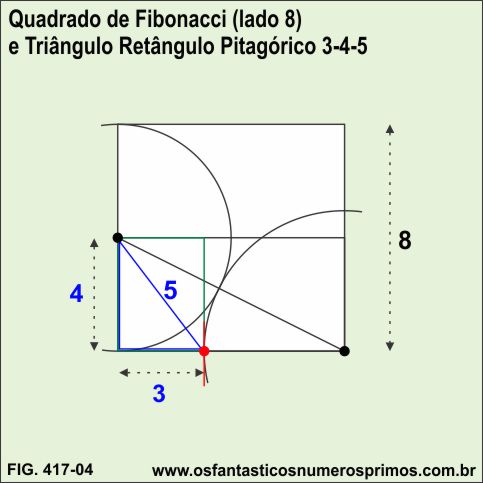
A pergunta que se faz é a seguinte: são possíveis de se encontrarem Triângulos Retângulos Pitagóricos a partir de Números de Fibonacci e a divisão em média e extrema razão cujos lado são números inteiros?
Autor: Ricardo Silva - dezembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato