


O WebSite Os Fantásticos Números Primos tem a honra de apresentar e convidá-lo(a) a participar de seus Desafios Geométricos e Matemáticos.
Em 2012, estudando para concurso públicos, encontrei na World Wide Web uma reportagem da Revista Superinteressante “A Inesgotável fonte dos números primos”, escrita pelo Professor da USP, Luiz Barco: no qual ele dizia: “quem ousar brincar com números descobrirá propriedades fascinantes”.
A partir daí comecei a perceber que números primos são números diferentes, então, pus me a pesquisá-los e a estudá-los.
Os números primos aguçam a nossa curiosidade, faz a gente ficar pensando, questionando..., fiz a primeira, a segunda, a terceira, a quarta, a quinta, a sexta, a sétima... pesquisa e ainda continuo pesquisando e estudando.
Os trabalhos de pesquisas e estudos foram crescendo, crescendo... e se enveredando por vários "caminhos", isto porque, assuntos, tópicos, hipóteses, conjecturas, teoremas e teorias matemáticas e geométricas estão interrelacionadas, um assunto vai "puxando" o outro.
E essas pesquisas e estudos possibilitaram interessantes descobertas matemáticas, ei-las:
Descobrir uma nova construção geométrica para se construir Triângulo Retângulo Pitagórico inscrito numa semicircunferência diferente das construções aqui apresentadas.
Para mais informações, veja matérias relacionadas abaixo.
Todo triângulo inscrito numa semicircunferência é triângulo retângulo.
Método geométrico universal
Triângulo retângulo de 30, 60 e 90 graus têm ângulos notáveis.
Traçando-se um arco de mesma medida do raio de uma semicircunferência em uma das extremidades do diâmetro, o ponto onde o arco intersecta a semicircunferência é o vértice cujo ângulo é 90 graus.
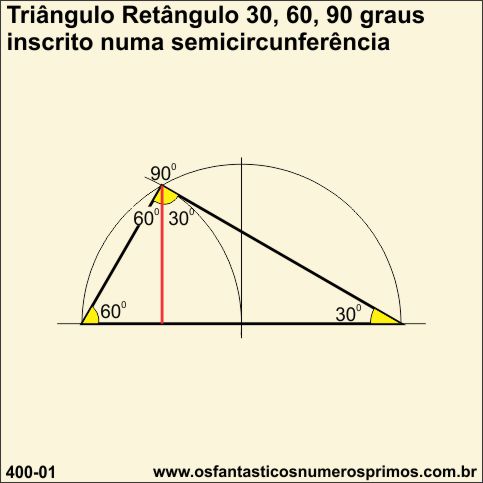
Método geométrico universal
Triângulo Retângulo Pitagórico é todo triângulo retângulo cujos lados são formados por números inteiros.
O primeiro Triângulo Retângulo Pitágórico têm seus lados formados pelo Terno Pitagórico 3, 4 e 5, uma sequência de três números inteiros consecutivos.
Triângulo Retângulo Pitagórico inscrito numa semicircunferência tem o seu maior lado que é a hipotenusa sobre o diâmetro da semicircunferência.
Para inscrever um Triângulo Retângulo Pitagórico, fazendo o uso de régua não graduada e compasso, numa semicircunferência de diâmetro arbritário, necessariamente tem que se fazer a divisão em partes iguais desse diâmetro e que corresponda a medida do termo de maior valor de um termo pitagórico o qual corresponde à medida da hipotenusa.
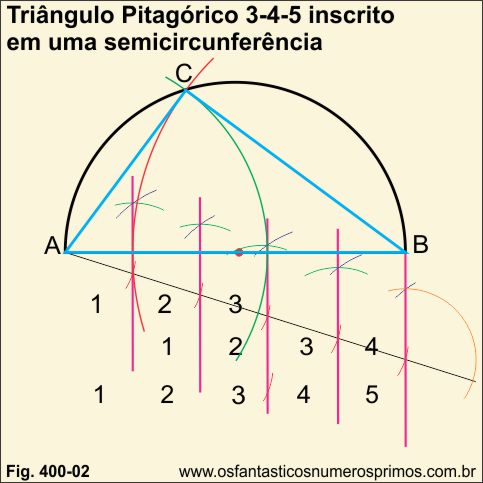
Novo Método
A partir de dois grupos de circunferências concêntricas e equidistantes sobre uma reta com distâncias entre as circunferências que correspondam a uma parte do termo de maior valor de um Terno Pitagórico ao se traçar uma semicircunfência cujas extremidades do diâmetro são os centros das circunferências concêntricas determinam-se dois pontos na semicircunferência que são os vértices de 90 graus dos Triângulos Retângulos Pitagóricos inscritos.
Interessante observar que também nessa construção são formadas as figuras geométricas da Vésica Piscis e da Mandorla.
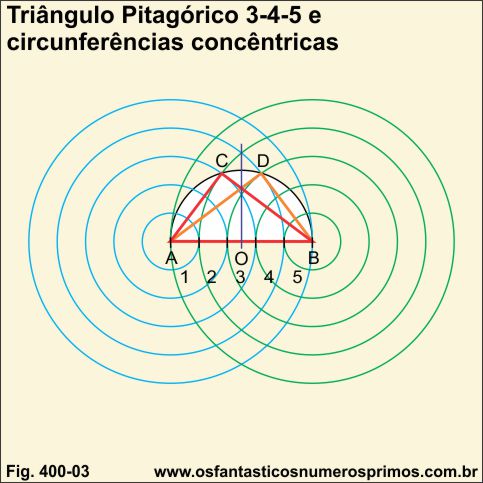
Veja matérias:
005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia
005-texto-018-triangulo-pitagorico-3-4-5-inscrito-semicircunferencia
Determinar diâmentro jacente ao plano a partir da própria circunferência.
Para mais informações, veja matérias relacionadas abaixo.
Dada uma circunferência de raio qualquer, é possível encontrar diâmetro jacente ao plano a partir da própria circunferência com régua não graduada e compasso?
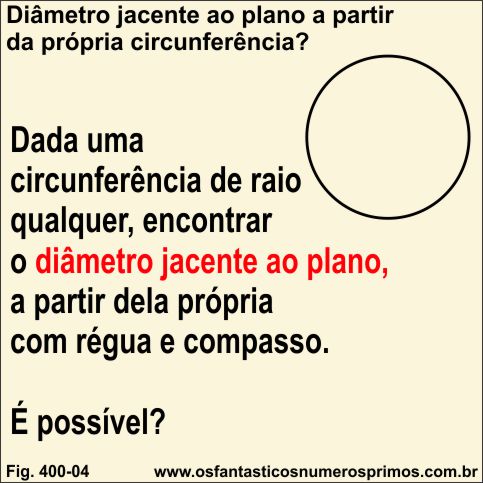
Veja matéria:
011-estudos-348-e-possivel-alinhar-circunferencia-em-um-plano-com-regua-compasso
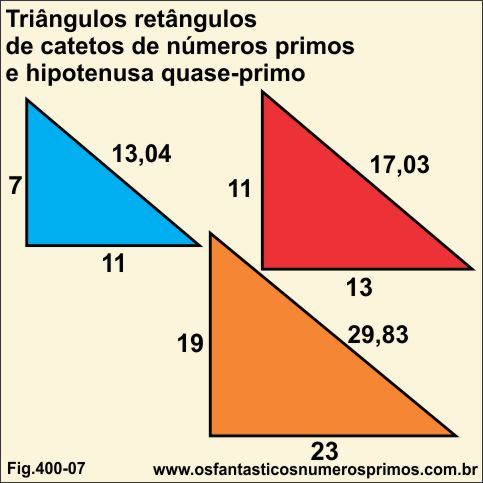
Construir triângulo retângulo de lados com medidas de números primos.
Para mais informações, veja matérias relacionadas abaixo.
Encontrou-se uma série de triângulos retângulos cujas medidas dos catetos são números primos e hipotenusas quase-primos.
Existe ao menos um triângulo retângulo cujos lados são formados por números primos?
Veja matéria:
011-estudos-354-triangulo-retangulo-de-lados-formados-numeros-primos-e-quase-primos
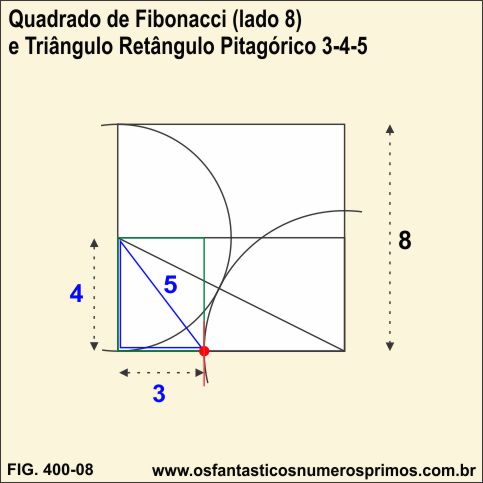
É possível encontrar outros Triângulos Retângulos Pitagóricos a partir de Números de Fibonacci e a divisão em média e extrema razão?.
Para mais informações, veja matérias relacionadas abaixo.
Veja matéria:
011-estudos-417-triangulo-retangulo-pitagorico-segmento-aureo
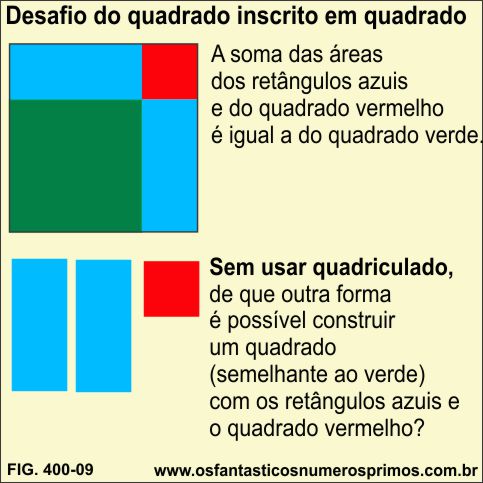
Desafio geométrico do quadrado inscrito em quadrado
Veja matéria:
011-estudos-417-triangulo-retangulo-pitagorico-segmento-aureo
Encontrar a próxima soma de dois números quadrados perfeitos consecutivos cujo resultado é também um número quadrado perfeito.

Veja matéria:
011-estudos-281-soma-dois-quadrados-perfeitos-consecutivos-multiplos-de-5
Descobrir um novo método para se calcular a medida da hipotenusa em Triângulo Retângulo Pitagórico por meio de cálculos numéricos sem utilizar o Teorema de Pitágoras diferentes das publicadas aqui no WebSite e no livro digital O Triângulo Retângulo.
Para mais informações, veja matérias relacionadas.

011-estudos-286-triangulo-pitagorico-calculos-de-catetos-hipotenusa
Quais números possuem entre seus divisores, quantidades em números primos como: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,...
Veja matéria:
011-estudos-095-divisores-de-um-numero-suas-regularidades-numericas
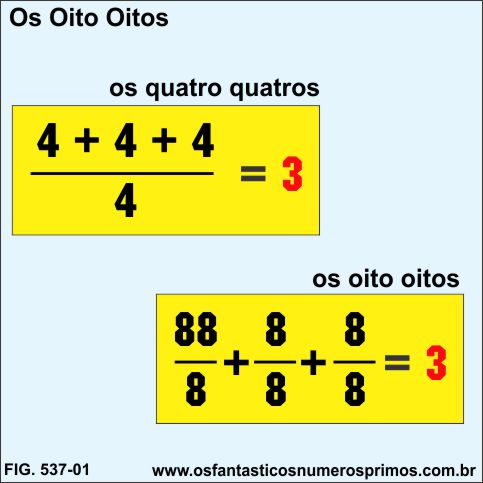
Gerar números naturais utilizando Os Oito Oitos.
Veja matéria:

Demonstrar a tese ou encontrar um contra exemplo:
| Tese: d divide n se e somente se d divide n'. |
No caso de um contra exemplo, envie uma Print de Tela da Calculadora (com números diferentes) para o e-mail:
contato@osfantasticosnumerosprimos.com.br e receberá como cortesia o livro digital: O Triângulo Retângulo - Novas Fórmulas Álgebricas e Aritméticas de Cálculos.
Veja calculadoras:
014-039-calculadora-particao-numero-multiplos-de-divisores-versao-adicao
014-040-calculadora-particao-numero-multiplos-de-divisores-versao-subtracao

Desenvolver algoritmo / fórmula que dada a medida hipotenusa, encontrar outros ternos pitagóricos.
Veja estudo:
011-estudos-628-numeros-fermat-4x+1-e-potencias
Autor: Ricardo Silva - setembro /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato