


A Sequência de Fibonacci é uma sequência numérica em que se repete o número 1 e partir do terceiro número somam-se dois números anteriores: 1, 1, 2, 3, 5, 8, 13, 21, 34,...
A Sequência de Fibonacci é uma sequência numérica que está estritamente relacionada ao Número de Ouro, pois dividindo-se um Número de Fibonacci por um número antecedente, o resultado é um número que tende ao Número Ф (Fi) :1,618033..., também denominado de Número Áureo, Número Dourado.
Os estudos publicados aqui no WebSite:
011-estudos-223-sequencia-fibonacci-e-ternos-pitagoricos
e
011-estudos-252-triangulos-fibonacci
discorrem de dois métodos que utilizando-se grupos de sequências de Números de Fibonacci e um outro Números não Fibonacci são possíveis de se construirem triângulos retângulos: um associado com ternos pitagóricos e o outro aos próprios números de Fibonacci.
O presente estudo demonstra um novo método de se construir triângulo retângulo associado a Terno Pitagórico, bem como, com seguimento áureo, escolhendo-se um número par da Sequência de Fibonacci.
a) divide-se o Número 8 de Fibonacci por 2, o quociente é 4;
b) subtrái-se o antecessor Número 5 de Fibonacci do Número 8 de Fibonacci; a diferença é o Número 3 de Fibonacci;
c) somam-se os quadrado de 3 e 4;
3² + 4² =
9 + 16 = 25
d) extrai-se a raiz quadrada de 25;
√25 = 5
3, 4 e 5 é um Terno Pitagórico Primitivo e com ele se forma o primeiro Triângulo Retângulo Pitagórico.
A tabela a seguir apresenta os 25 primeiros Números de Fibonacci e entre eles, o método exposto acima e aplicado a números pares.
Interessante observar que:
a) Números de Fibonacci geraram a raiz quadrada de 2 (√2);
b) exeto a raiz quadrada de 25 que é 5, um número inteiro, os demais resultados são todos números irracionais;
A pergunta que se faz é a seguinte: haverá outro número par de Fibonnaci que aplicando o método acima ter-se-á raiz quadrada um número inteiro?
| Números pares | ||||||
| de Fibonacci | ||||||
| Número | metade | diferença | quadrados | soma | raiz | |
| Fibonacci | de | quadrada | ||||
| quadrados | ||||||
| 1 | ||||||
| 1 | ||||||
| 2 | 1 | 1 | 1 | 1 | 2 | 1,41421 |
| 3 | ||||||
| 5 | ||||||
| 8 | 4 | 3 | 16 | 9 | 25 | 5 |
| 13 | ||||||
| 21 | ||||||
| 34 | 17 | 13 | 289 | 169 | 457 | 21,389 |
| 55 | ||||||
| 89 | ||||||
| 144 | 72 | 55 | 5184 | 3025 | 8209 | 90,606 |
| 233 | ||||||
| 377 | ||||||
| 610 | 305 | 233 | 93025 | 54289 | 147313 | 383,814 |
| 987 | ||||||
| 1.597 | ||||||
| 2.584 | 1292 | 987 | 1669264 | 974169 | 2643433 | 1625,863 |
| 4.181 | ||||||
| 6.765 | ||||||
| 10.946 | 5473 | 4181 | 29953729 | 17480761 | 47434490 | 6887,270 |
| 17.711 | ||||||
| 28.657 | ||||||
| 46.368 | 23184 | 17711 | 537497856 | 313679521 | 851177378 | 29174,944 |
| www.osfantasticosnumeros primos.com.br | ||||||
Os 6 primeiros ternos da Sequência de Fibonacci são:1, 1, 2, 3, 5, 8,...
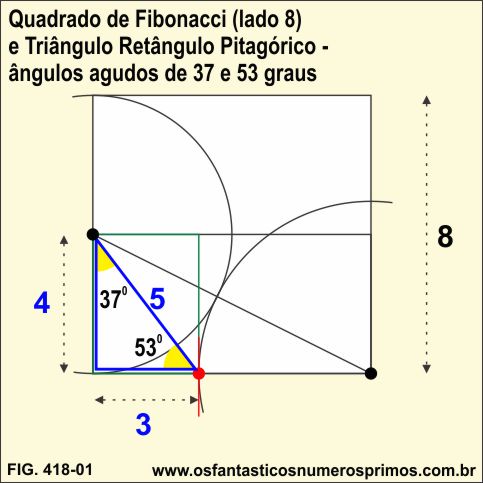
Construindo-se um quadrado de lado 8 (Número de Fibonacci), dividindo-o ao meio e determinando a divisão em média e extrema razão, a partir do ponto áureo, o triângulo formado (cor azul) é um Triângulo Retângulo cujos ângulos agudos são aproximadamente 37 e 53 graus e que são ângulos agudos de um Triângulo Retângulo Pitagórico 3-4-5.
Autor: Ricardo Silva - janeiro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato