


Equações Diofantinas são equações na forma ax + bx = c cujas soluções são números inteiros e que foram estudadas por Diofanto de Alexandria (nascido entre 201 e 214 - falecido entre 284 e 298 d.C), matemático grego considerado "Pai da Álgebra" e o primeiro matemático a utilizar símbolos para representar incógnitas (números desconhecidos) em equações.
Na vídeo-aula Aritmética - 28 - Equações Diofantinas: Quando existe solução? do Programa de Iniciação Científica - PIC da OBEMP, o Professor Fábio Henrique faz demonstrações de como resolver o seguinte problema que envolve Equação Diofantina:
De quantos modos podemos comprar selos de R$ 5,00 e de R$ 3,00 de modo a gastar, ao todo, R$ 50,00...
...o qual é solucionado conforme etapas a seguir de forma que os resultados têm que serem números inteiros positivos, pelo fato de se estar operando com valores monetários.
a) 5x - 3y = 50
b) substituindo x por 10, podemos comprar 10 selos de R$ 5,00 e nada de R$ 3,00 e tem-se a primeira solução da equação;
5.(10) - 3.(0) = 50
c) substituindo x por 7, y por 5, podemos comprar 7 selos de R$ 5,00 e 5 de R$ 3,00 e tem-se a segunda solução da equação;
5.(7) - 3.(5) = 50
d) substituindo x por 4, y por 10, podemos comprar 4 selos de R$ 5,00 e 10 de R$ 3,00 e tem-se a terceira solução da equação;
5.(4) - 3.(10) = 50
e) substituindo x por 1, y por 15, podemos comprar 1 selos de R$ 5,00 e 15 de R$ 3,00 e tem-se a quarta solução da equação;
5.(1) - 3.(15) = 50
Montando-se uma tabela das soluções da Equação Diofantina acima, notam-se padrões e regularidades nas sequências dos números das incógnitas, vejamos:
a) na coluna do (x), os números, a partir do 10, vão diminuindo de 3 em 3 unidades;
b) 3 é o coeficiente de y (3y);
c) na coluna do (y), os números, a partir do 0, vão aumentando de 5 em 5 unidades;
d) 5 é coeficiente de x (5x).
| Tabela 1 | |||
| Soluções da Equação Diofantina | |||
| 5x - 3y = 50 | |||
| incógnita | incógnita | ||
| x | y | ||
| 10 | 0 | ||
| - 3 | + 5 | ||
| 7 | 5 | ||
| - 3 | + 5 | ||
| 4 | 10 | ||
| - 3 | + 5 | ||
| 1 | 15 | ||
| www.osfantasticosnumerosprimos.com.br | |||
Neste outro exemplo, o Professor Fábio Henrique demonstra como resolver Equação Diofantina que contêm a seguinte propriedade: "Toda Equação Diofantina tem solução se e somente se o mdc (a,b) divide c":
4x + 6y = 10
a) determina-se o Máximo Divisor Comum de 4 e 6;
mdc (4, 6) = 2
b) o mdc 2 divide o termo 10 (c);
c) a equação 4x + 6y = 10 tem solução;
d) divide-se cada termo da equação 4x - 6y = 10 pelo mdc 2;
e) obtêm-se uma equação reduzida, isto é, uma equação mais simplificada: 2x + 3y = 5;
f) na nova equação 2x + 3y = 5, 2 e 3 são números primos entre si, pois o mdc (2, 3) = 1;
a) substituindo x por 1, y por 1, tem-se a primeira solução da equação;
2(1) + 3(1) = 5
b) substituindo x por 4, y por -1, tem-se a segunda solução da equação;
2(4) + 3(-1) = 5
c) substituindo x por 7, y por -3, tem-se a segunda solução da equação;
2(7) + 3(-3) = 5
Montando-se uma tabela das soluções da Equação Diofantina acima, notam-se padrões e regularidades nas sequências dos números das incógnitas, vejamos:
a) na coluna do (x), os números, a partir do 1, vão aumentando de 3 em 3 unidades;
b) 3 é o coeficiente de y (3y);
c) na coluna do (y), os números, a partir do 1, vão aumentando de 2 em 2 unidades;
d) 2 é coeficiente de x (2x).
| Tabela 2 | |||
| Soluções da Equação Diofantina | |||
| 2x - 3y = 5 | |||
| incógnita | incógnita | ||
| x | y | ||
| 1 | 1 | ||
| + 3 | - 2 | ||
| 4 | - 1 | ||
| + 3 | - 2 | ||
| 7 | - 3 | ||
| www.osfantasticosnumerosprimos.com.br | |||
O Professor Fábio Henrique demonstra também que podemos encontrar mais e mais soluções, isto é, infinitas soluções, para a equação 2x + 3y = 5, entendendo-os cálculos verticalmente para cima e para baixo em ambas colunas das incógnitas (x) e (y).
| Tabela 3 - Extendida | |||
| Soluções da Equação Diofantina | |||
| 2x - 3y = 5 | |||
| incógnita | incógnita | ||
| x | y | ||
| - 5 | + 5 | ||
| -3 | + | ||
| - 2 | 3 | ||
| - 3 | + 2 | ||
| 1 | 1 | ||
| + 3 | - 2 | ||
| 4 | - 1 | ||
| + 3 | - 2 | ||
| 7 | - 3 | ||
| + 3 | - 2 | ||
| 10 | - 5 | ||
| + 3 | - 2 | ||
| 13 | - 7 | ||
| + 3 | - 2 | ||
| 16 | - 9 | ||
| + 3 | - 2 | ||
| 19 | - 11 | ||
| + 3 | - 2 | ||
| 22 | - 13 | ||
| www.osfantasticosnumerosprimos.com.br | |||
A Equação Diofantina 2x + 3y = 5 têm seus coefientes, os números 2 e 3 e o termo (c), números primos.
É uma equação reduzida, isto é, originada da equação 4x + 6y = 10.
Observando com mais detalhes a Tabela 3 - Extendida, na coluna da incógnita (x), a sequência numérica gerada em sentido vertical para baixo, a partir do número 1, tem entre seus termos a Sequência de Números Figurados Triangulares Centrados:
1, 4, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46,...
Números Figurados Triangulares Centrados são números figurados formando triângulos equidistantes a partir de um ponto central e com os demais pontos formando os vértices e os lados desses triângulos também em espaços equidistantes.
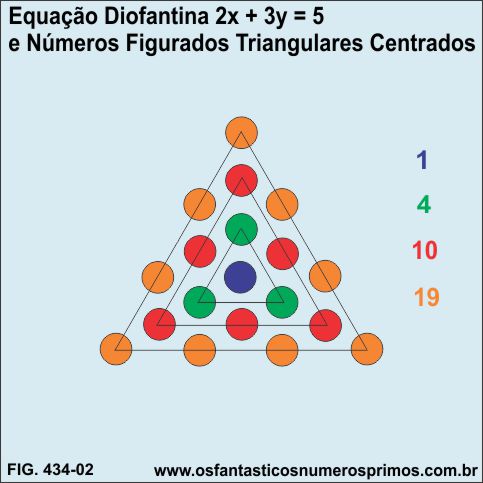
Elaborando-se outra tabela e desconsidenrando os sinais negativos dos termos da incógnita (y), as sequências numéricas formadas apresentam outras regularidades numéricas:
a) os termos da incógnita (y) formam a sequência de números ímpares;
b) determinados números figurados triangulares centrados que aparecem intercalados na sequência formada por termos da incógnita (x) estão alinhados a números primos da sequência formada por termos da incógnita (y) - células amarelas;
c) quando um número figurado triangular centrado é multiplo de 5, então esse triangular centrado aparece alinhado a um outro múltiplo de 5 na coluna de termos da incógnita (y) - células laranjas.
d) determinados números figurados triangulares centrados também são números primos: 19, 31, 109, 199, 571,...
| Tabela 4 | |
| Sequências Numéricas | |
| geradas da | |
| Equação Diofantina | |
| 2x - 3y = 5 | |
| números ímpares | |
| Termos da | Termos da |
| incógnita x | incógnita y |
| 1 | 1 |
| 4 | 1 |
| 7 | 3 |
| 10 | 5 |
| 13 | 7 |
| 16 | 9 |
| 19 | 11 |
| 22 | 13 |
| 25 | 15 |
| 28 | 17 |
| 31 | 19 |
| 34 | 21 |
| 37 | 23 |
| 40 | 25 |
| 43 | 27 |
| 46 | 29 |
| 49 | 31 |
| 52 | 33 |
| 55 | 35 |
| 58 | 37 |
| 61 | 39 |
| 64 | 41 |
| 67 | 43 |
| 70 | 45 |
| 73 | 47 |
| 76 | 49 |
| 79 | 51 |
| 82 | 53 |
| 85 | 55 |
| 88 | 57 |
| 91 | 59 |
| 94 | 61 |
| 97 | 63 |
| 100 | 65 |
| 103 | 67 |
| 106 | 69 |
| 109 | 71 |
| 112 | 73 |
| 115 | 75 |
| 118 | 77 |
| 121 | 79 |
| 124 | 81 |
| 127 | 83 |
| 130 | 85 |
| 133 | 87 |
| 136 | 89 |
| www.osfantasticosnumerosprimos.com.br | |
Para mais informações, veja matérias relacionadas, sobre números figurados, abaixo.
Autor: Ricardo Silva - junho/2023
ROSA, Telia Mara Lopes da. Equações Diofantinas: Uma proposta de atividade para o Ensino Fundamental. TCC - Licenciatura Matemática junto ao Instituto de Matemática, Física e Estatística da Universidade Federal do Rio Grande.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/wiki/Diofanto
https://pt.wikipedia.org/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato