A Sequência de Fibonacci é uma sequência numérica em que se repete o número 1 duas vezes e a partir do terceiro termo somam-se dois números anteriores: (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...). É uma sequência numérica que possui diversas propriedades algébricas e aritméticas relacionadas à matemática, à geometria, à física, à biologia, à química, etc.
Em 1976, o químico japonês, Haruo Hosoya publicou um artigo no Periódico Fibonacci Quarterly de um triângulo equilátero com números da Sequência de Fibonacci conforme explanações a seguir:
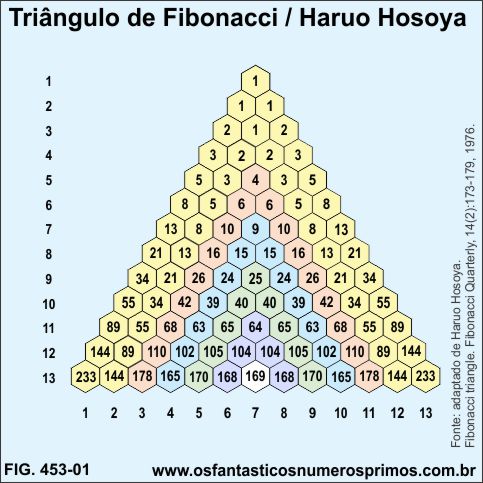
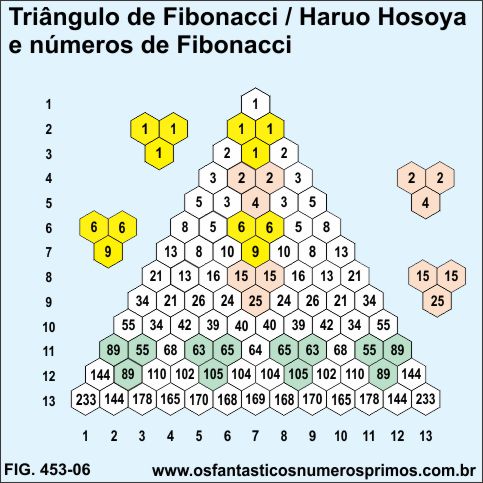
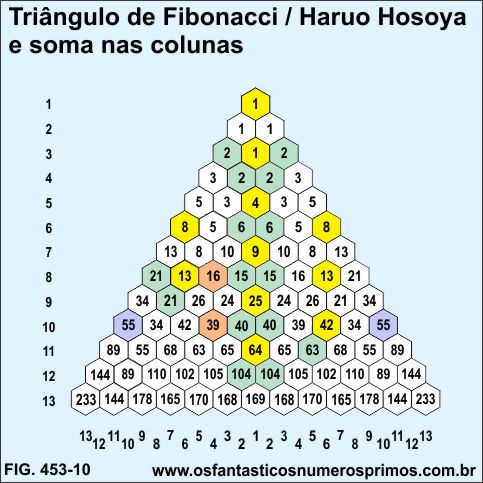
a) o lado esquerdo, do topo para a base do triângulo, são formados por duas Sequências de Fibonacci (células amarelas);
b) o lado direito, do topo para a base do triângulo, também são formados por suas Sequências de Fibonacci (células amarelas);
c) acompanhando o alinhamento das células amarelas, tanto à da esquerda quanto à da direita, as demais linhas coloridas, vice-versa, são as somas a partir de dois termos da Sequência de Fibonacci;
2, 2, 4, 6, 10, 16, 26, 42, 68, 110, 178,... (células laranjas);
3, 3, 6, 9, 15, 24, 39, 63, 102, 165,... (células azuis);
5, 5, 10, 15, 25, 40, 65, 105, 170, ... (células: laranja, azui e verdes) e assim sucessivamente;
d) os termos são simetricamente distribuídos dentro do triângulo.
e) em cada sequência, os termos são múltiplos de números de Fibonacci, isto é, um número constante de Fibonacci multiplicados pela própria Sequência de Fibonacci;
2, 2, 4, 6, 10, 16, 26, 42, 68, 110, 178,... (células laranjas);
2 x 1 = 2
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 5 = 10
e assim sucessivamente.
O Triângulo de Fibonacci / Haruo Hosoya também apresenta diversas propriedades algébricas e aritméticas semelhantes ao Triângulo de Pascal, eis algumas delas:
Os números triangulares consecutivos 3, 6, 10 e 15 aparecem quase no topo do triângulo.
Interessante observar que:
3 + 6 (triangulares) = 9 (quadrado perfeito)
10 + 15 (triangulares) = 25 (quadrado perfeito)
Números de Fibonacci que também são números triangulares estão acompanhados de seus respectivos números retangulares simetricamente.
1 e 1 está acompanhado de 2.
3 e 3 está acompanhado de 6.
21 e 21 está acompanhado de 42.
55 e 55 está acompanhado de 110.
Os números quadrados perfeitos 1, 4, 9, 25, 64,... aparecem na altura do triângulo equilátero.
Os números quadrados perfeitos 1, 4, 9, 25, 64,... aparecem em linhas ímpares.
Os números quadrados perfeitos 1, 4, 9, 25, 64 são os quadrados perfeitos dos números de Fibonacci: 1, 2, 3, 5, 8, 13, ...
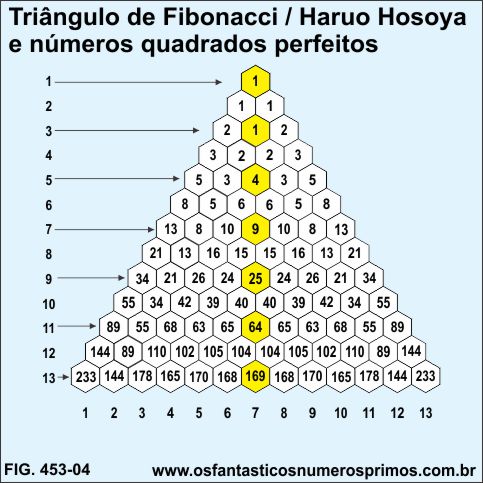
Juntando-se 4 células em formato de "cruz" a partir do topo da altura do triângulo e somando-se os números, os resultados são números quadrados perfeitos...
1 + 1 + 1 + 1 = 4
1 + 2 + 2 + 4 = 9
4 + 6 + 6 + 9 = 25
9 + 15 + 15 + 25 = 64
25 + 40 + 40 + 64 = 169
... cujas raízes quadradas são números de Fibonacci: 2, 3, 5, 8, 13, ...
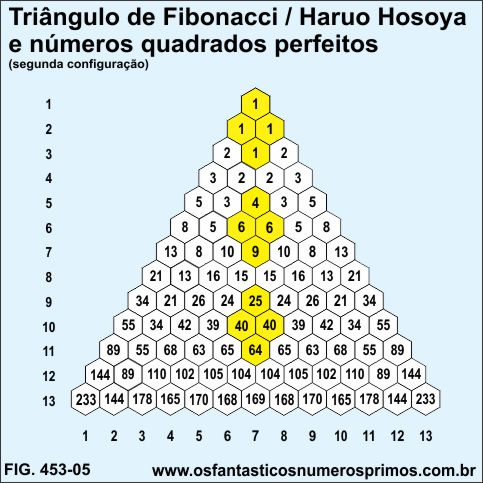
A soma de dois números quadrados perfeitos consecutivos do Triângulo de Fibonacci / Haruo Hosoya têm como resultados também números de Fibonacci que se encontram simetricamente em linhas e colunas ímpares.
Exemplos:
1 + 1 = 2
1 + 4 = 5
4 + 9 = 13
9 + 25 = 34
2, 5, 13, 34, ... são números de Fibonacci.
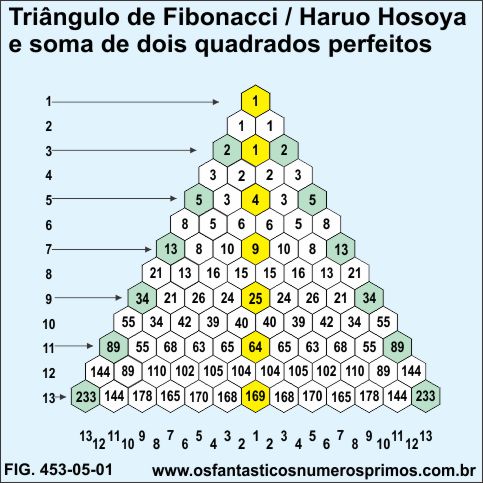
Juntando-se três células em formato de triângulo invertido e somando-se os números, o resultado é um número de Fibonacci.
Exemplos:
1 + 1 + 1 = 3
2 + 2 + 4 = 8
6 + 6 + 9 = 21
A soma de quaisquer dois números em uma linha e outro na linha abaixo centralizado formando um triângulo invertido, tem como resultado um número constante de Fibonacci (células verdes).
Exemplos:
89 + 55 + 89 = 233
55 + 68 + 110 = 233
68 + 63 + 102 = 233
François-Édouard-Anatole Lucas (1842-1891), matemático francês e estudioso das obras de Leonardo de Pisa foi quem popularizou os Números de Fibonacci em sua obra Recherches Sur Plusierurs Ouvrages de Léonard de Pisa (1877) e que através dela criou outra sequência semelhante chamada de Sequência de Lucas: 2, 1, 3, 4, 7, 11, 18,...
Outro feito, foi ter descoberto o 120 número primo de Mersenne com 39 dígitos:
M127 = 2127-1
= 17.141.183.404.
e que permanece como recorde (75 anos), tal descoberta sem uso de computador.[2]
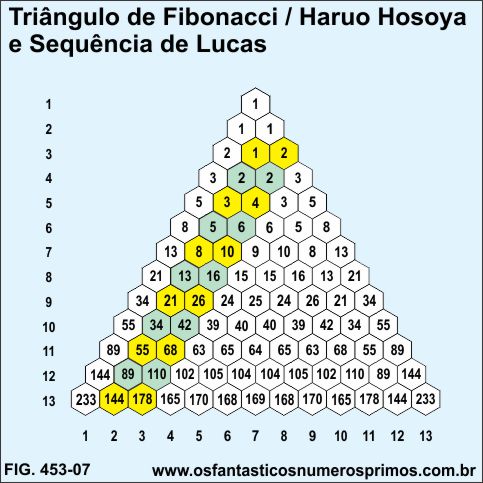
Somando-se dois números em cada linha; um número de Fibonacci e um múltiplo de 2 (número 2 multiplicado com um número de Fibonacci), obtêm-se Números de Lucas a partir do terceiro termo:
1 + ( 2 x 1 ) = 3
2 + ( 2 x 1 ) = 4
3 + ( 2 x 2 ) = 7
5 + ( 2 x 3 ) = 11
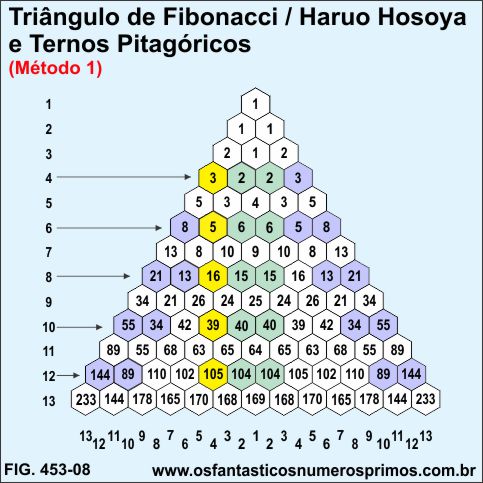
A partir da linha 4 e assim para linhas pares, são possíveis de se formarem ternos pitagóricos primitivos e derivados no Triângulo de Fibonacci / Haruo Hosoya.
Nas linhas cujas ordens são pares, a soma dos dois números de Fibonacci, dos extremos do lado esquerdo ou do lado direito do Triângulo de Fibonacci / Haruo Hosoya, são números que correspondem às hipotenusas em triângulos retângulos (células roxas); os números repetidos que somados, juntos a coluna central, correspondem aos catetos maiores (células verdes); e os números aos lados de números que se repetem são os que correspondem aos cateto menores (células amarelas).
| Triângulo de Fibonacci / | |||||||||||
| Haruo Hosoya | |||||||||||
| e | |||||||||||
| Ternos Pitagóricos | |||||||||||
| Números | ternos | ||||||||||
| do triângulo | pitagóricos | ||||||||||
| Fibonacci | |||||||||||
| catetos | hipo- | hipo- | |||||||||
| tenusa | catetos | tenusa | |||||||||
| c | b | b | a | a | c | b + b | a + a | c² | b² | b²+ c² | a² |
| 3 | 2 | 2 | 2 | 3 | 3 | 4 | 5 | 9 | 16 | 25 | 25 |
| 5 | 6 | 6 | 5 | 8 | 5 | 12 | 13 | 25 | 144 | 169 | 169 |
| 16 | 15 | 15 | 13 | 21 | 16 | 30 | 34 | 256 | 900 | 1156 | 1156 |
| 39 | 40 | 40 | 34 | 55 | 39 | 80 | 89 | 1521 | 6400 | 7921 | 7921 |
| 105 | 104 | 104 | 89 | 144 | 105 | 208 | 233 | 11025 | 43264 | 54289 | 54289 |
| 272 | 273 | 273 | 233 | 377 | 272 | 546 | 510 | 73984 | 298116 | 372100 | 372100 |
| 715 | 714 | 714 | 610 | 987 | 715 | 1428 | 1597 | 511225 | 2039184 | 2550409 | 2550409 |
| www.osfantasticosnumerosprimos.com.br | |||||||||||
Observação: Cada dupla de números de Fibonacci, a partir da dupla 3 e 5, formam os termos m e n das Fórmulas de Euclides com as quais são possíveis de se gerarem ternos pitagóricos.
Para mais informações, veja matérias relacionadas abaixo.
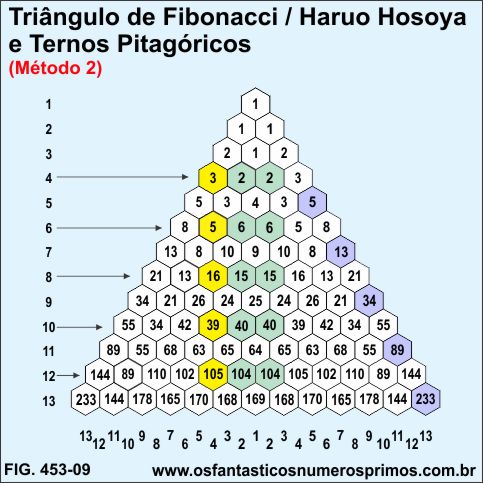
SMITH, Jeffrey Lee [3], em sua tese de mestrado, de modo diferente, para formar ternos pitagóricos, pega o termo que corresponde à hipotenusa, o último elemento da linha abaixo dos dois termos que correspondem aos catetos no triângulo retângulo.
Exemplo:
Para formar o Terno Pitagórico 3-4-5, pegam-se os números na linha 4: 3 (célula amarela), 2 e 2 (células verdes) e 5 (célula roxa) na linha 5;
As somas de termos em colunas no Triângulo de Fibonacci / Haruo Hosoya apresentam métodos e propriedades numéricas específicas, vejamos:
a) na coluna central (altura do triângulo equilátero), excluindo a soma dos quadrados 1 e 1 cujos resultados aparecem abaixo e nas laterais do quadrado 1, as somas consecutivas a partir de 3 números quadrados aparecem abaixo do último quadrado somado (última parcela);
Exemplos:
1 + 1 = 2
a soma 2 aparece duas vezes abaixo e ao lado da última parcela 1.
1 + 1 + 4 = 6
a soma 6 aparece duas vezes abaixo da última parcela 4.
b) quando se somam dois números; sendo que o primeiro número esteja "encostado" nos lados esquerdo ou direito do triângulo, então a soma está abaixo e ao lado da última parcela;
Exemplo:
8 + 13 = 21
a soma 21 aparece abaixo e ao lado do 13.
c) quando se somam dois números; sendo que o primeiro número não esteja "encostado" nos lados do triângulo, então a soma está nos lados do triângulo;
Exemplos:
13 + 42 = 55
16 + 39 = 55
como o triângulo é simétrico, a soma 55 se encontra no lado esquerdo quanto no direito.
d) quando se somam 3 números ou mais; sendo que o primeiro esteja "encostado" nos lados do triângulo, então a soma está abaixo e ao lado da última parcela;
Exemplos:
8 + 13 + 42 = 63
como o triângulo é simétrico, a soma 63 se encontra no lado esquerdo qunto no direito.
1 + 2 + 6 + 15 = 24 (soma de somas de quadrados)
a soma 24 está abaixo da parcela 15, como o triângulo é simétrico, a soma 24 se encontra em posições esquerda e direita.
e) quando se somam 3 números ou mais, sendo que o primeiro número não esteja "encostado" nos lados do triângulo, então a soma é parte de números consecutivos da linha abaixo da última parcela;
Exemplo 1)
2 + 6 + 15 = 23
a soma 23 não se encontra no triângulo.
23 é 1 unidade menor que 24.
23 é 2 unidades menor que 25.
24 e 25 se encontram abaixo da parcela 15.
1 e 2 são números de Fibonacci.
23 é "complemento" dos números 24 e 25 na tabela, pois forma uma progressão aritmética finita: (23, 24, 25).
Exemplo 2)
2 + 6 + 15 + 40 = 63
a soma 63 não se encontra no triângulo.
63 é 1 unidade menor que 64.
63 é 2 unidades menor que 65.
64 e 65 se encontram abaixo de 40.
1 e 2 são números de Fibonacci.
63 é "complemento" dos números 64 e 65 na tabela, pois forma uma progressão aritmética finita: (63, 64, 65).
Autor: Ricardo Silva - julho/2023
[2] ASTROLINO e SILVA, Bruno. Números de Fibonacci e números de Lucas. Dissertação (Mestrado de Pós Graduação em Mestrado Profissional em Matemática em Rede Nacional) --Instituto de Ciências Matemáicas e de Computação, Universidade de São Paulo, 2017.
HOSOYA, Haruo. Fibonacci triangle. Fibonacci Quarterly, 14(2):173-179, 1976.
[3]SMITH, Jeffrey Lee, "The Fibonacci sequence and Hosoya's triangle" (2013). Theses Digitization Project . 3975.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
