


Números Triangulares fazem parte de um grupo de sequências numéricas denominados de números figurados ou também números geométricos que a partir de arranjos de pontos podemos formar figuras geométricas de triângulos.
Há dois métodos tradicionais de se obterem números triangulares:
a) por meio da soma de números naturais consecutivos;
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
b) do produto de dois números consecutivos dividido por 2;
(1 x 2) / 2 = 1
(2 x 3) / 2 = 3
(3 x 4) / 2 = 6
(4 x 5) / 2 = 10
Aqui no WebSite Os Fantáticos Números Primos, bem como, na coleção de livros digitais sobre sequências numéricas aqui divulgados, há diversos outros estudos e métodos em que são possíveis de obterem números triangulares.
Para mais informações, veja matérias relacionadas abaixo.
Recentemente recebi do Sr. Aristóteles de Araujo Costa, residente em Teresina - PI, o link do vídeo:
https://youtu.be/leCuEKti5U8
no qual ele demonstra um dispositivo numérico em formato de triângulo construído com sequências de dois números ímpares repetidos com o qual são possíveis também de obterem números triangulares.
Segundo o Sr. Aristóteles, a construção do dispositivo, o qual ele denomina de Escada de Dois Degraus Para Números Triangulares se baseou na leitura do livro digital Números Triangulares e Sequências Numéricas.
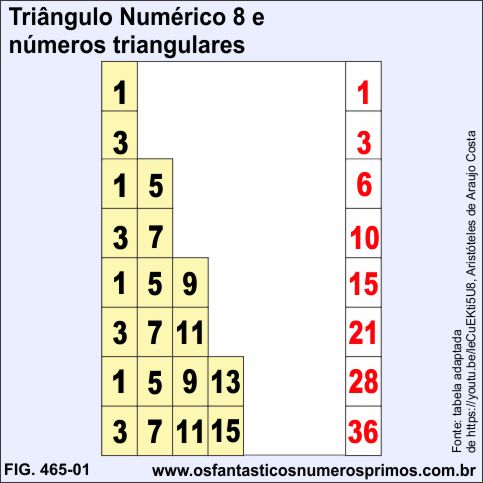
O WebSite Os Fantásticos Números Primos, tomou a liberdade de nomear o dispositivo Escada de Dois Degraus Para Números Triangulares para Triângulo Numérico 8 e Números Triangulares por questão organização e ordem e também pelo fato de haver outros dispositivos numéricos semelhantes a triângulos.
| Triângulo Numérico 8 | |||||||||||
| e | |||||||||||
| Números Triangulares | |||||||||||
| linhas | colunas | soma | |||||||||
| 1 | 1 | 1 | |||||||||
| 2 | 3 | 3 | |||||||||
| 3 | 1 | 5 | 6 | ||||||||
| 4 | 3 | 7 | 10 | ||||||||
| 5 | 1 | 5 | 9 | 15 | |||||||
| 6 | 3 | 7 | 11 | 21 | |||||||
| 7 | 1 | 5 | 9 | 13 | 28 | ||||||
| 8 | 3 | 7 | 11 | 15 | 36 | ||||||
| 9 | 1 | 5 | 9 | 13 | 17 | 45 | |||||
| 10 | 3 | 7 | 11 | 15 | 19 | 55 | |||||
| 11 | 1 | 5 | 9 | 13 | 17 | 21 | 66 | ||||
| 12 | 3 | 7 | 11 | 15 | 19 | 23 | 78 | ||||
| 13 | 1 | 5 | 9 | 13 | 17 | 21 | 25 | 91 | |||
| 14 | 3 | 7 | 11 | 15 | 19 | 23 | 27 | 105 | |||
| 15 | 1 | 5 | 9 | 13 | 17 | 21 | 25 | 29 | 120 | ||
| 16 | 3 | 7 | 11 | 15 | 19 | 23 | 27 | 31 | 136 | ||
| 17 | 1 | 5 | 9 | 13 | 17 | 21 | 25 | 29 | 33 | 153 | |
| 18 | 3 | 7 | 11 | 15 | 19 | 23 | 27 | 31 | 35 | 171 | |
| 19 | 1 | 5 | 9 | 13 | 17 | 21 | 25 | 29 | 33 | 37 | 190 |
| 20 | 3 | 7 | 11 | 15 | 19 | 23 | 27 | 31 | 35 | 39 | 210 |
Fonte: tabela adaptada de https://youtu.be/
a) cada coluna é formada por dois números ímpares consecutivos repetidos;
Exemplos:
1, 3, 1, 3, 1, 3, 1, 3, ...
5, 7, 5, 7, 5, 7, 5, 7, ...
9, 11, 9, 11, 9, 11, 9, 11, ...
b) cada coluna de sequências de dois ímpares repetidos começam em linha ímpares;
c) a soma de cada linha que é constituída de números ímpares "intercalados" têm como resultados números triangulares;
Exemplos:
1, 5, 9, 13, 17, 21, 25, 29, 33, 37, ...
3, 7, 11, 15, 19, 23, 27, 31, 35, 39, ...
d) as linhas formam duas progressões aritméticas de razão 4; uma de termo inicial 1 e outra de termo inicial 3;
1, 5, 9, 13, 17, 21, 25, 29, 33, 37, ...
3, 7, 11, 15, 19, 23, 27, 31, 35, 39, ...
e) cada número triangular tem a sua ordem / posição natural;
Exemplos:
1 é o primeiro triangular e se encontra na linha 1;
3 é o segundo triangular e se encontra na linha 2;
6 é o terceiro triangular e se encontra na linha 3.
Construíndo-se um triângulo numérico semelhante ao Triângulo Numérico 8 com termos da Sequência de Fibonacci observa-se novamente uma interessante propriedade relacionada a própria Sequência de Fibonacci de que a soma de termos intercalados de números de Fibonacci geram também números de Fibonacci, vejamos:
a) nas linhas impares, a soma de termos intercalados da Sequência de Fibonacci têm como resultados números de Fibonacci de ordens / posições pares;
b) nas linhas pares, a soma de termos intercalados da Sequência de Fibonacci têm como resultado números de 1 unidade menor de um número de Fibonacci, a partir da linha 4.
Os primeiros 12 números da Sequência de Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,...
| Triângulo Numérico 9 | |||||||||
| e | |||||||||
| Sequência de Fibonacci | |||||||||
| linhas | colunas | soma | |||||||
| 1 | 1 | 1 | |||||||
| 2 | 1 | 1 | |||||||
| 3 | 1 | 2 | 3 | ||||||
| 4 | 1 | 3 | 4 | ||||||
| 5 | 1 | 2 | 5 | 8 | |||||
| 6 | 1 | 3 | 8 | 12 | |||||
| 7 | 1 | 2 | 5 | 13 | 21 | ||||
| 8 | 1 | 3 | 8 | 21 | 33 | ||||
| 9 | 1 | 2 | 5 | 13 | 34 | 55 | |||
| 10 | 1 | 3 | 8 | 21 | 55 | 88 | |||
| 11 | 1 | 2 | 5 | 13 | 34 | 89 | 144 | ||
| 12 | 1 | 3 | 8 | 21 | 55 | 144 | 232 | ||
| 13 | 1 | 2 | 5 | 13 | 34 | 89 | 233 | 377 | |
| 14 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 609 | |
| 15 | 1 | 2 | 5 | 13 | 34 | 89 | 233 | 610 | 987 |
| 16 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 1596 |
| www.osfantasticosnumerosprimos.com.br | |||||||||
Autor: Ricardo Silva - agosto/2023
COSTA, Aristóteles de Araujo. Escada de Dois Degraus Para Números Triangulares.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato