Página de estudos de matemática e sequências numéricas

Triângulos Numéricos dos Arquitetos Medievais e extrações de raízes quadradas - 451

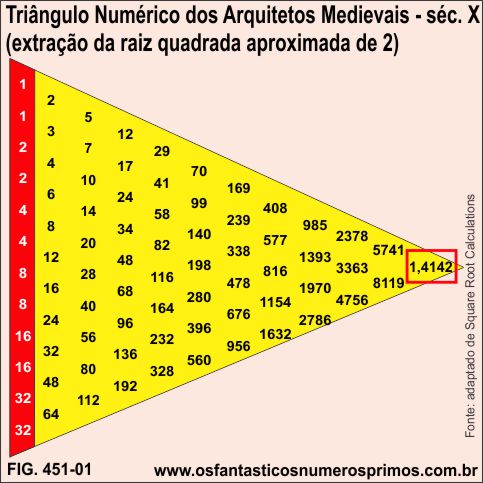
A estudante de arquitetura da Universidade da California - Los Angeles - UCLA - EUA, Sukuru Yuksel, pesquisando sobre como os arquitetos europeus do século X faziam para encontrar raízes quadradas, se deparou com o seguinte algoritmo: [1]

a) a partir de uma progressão geométrica de razão 2:

1, 2, 4, 8, 16, 32,...

b) intercala-se multiplicações de termos da PG com a raiz quadrada de 2;

1, 1√2, 2, 2√2, 4, 4√2, 8, 8√2, 16, 16√2, 32, 32√2,...

c) determina-se a raiz quadrada de 2 em 1 unidade e elabora-se os produtos;

d) obtendo uma nova sequência numérica:

1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32

e) posteriormente, somam-se de dois em dois termos, e os resultado são colocados entre os termos em novas linhas, conforme o dispositivo numérico, abaixo.

Na verdade, obtem-se um triângulo de base e topo invertidos.

Uma das propriedades do Triângulo Numérico Invertido dos Arquitetos Medievais do Século X e que a razão entre os dois números finais (topo invertido):

8119 / 5741 = 1,414213552....

tem como resultado a raiz quadrada de 2 com uma aproximação de 7 casas decimais.

Uma outra importante propriedade do Triângulo Numérico Invertido dos Arquitetos Medievais do Sérculo X é que as duas sequências de números da lateral esquerda são as mesmas do Algortimo da Escada de Theon para a extração da raiz quadrada aproximada de 2 (células laranjas).

Para mais informações, veja matérias relacionadas abaixo.

Fonte: adaptado de Square Root Calculations [1]

Triângulo numérico e extração da raiz quadrada de 2

Reconfigurando o Triângulo Numérico Invertido dos Arquitetos Medievais do Século X para a extração da raiz quadrada aproximada de 2, conforme modelo abaixo, podê-se deixá-lo mais compacto e melhor para se visualizar suas informações e propriedades.

A partir da sequência numérica: 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32 posta em sentido vertical, foram então somados de dois em dois termos e os resultados intercalados de forma que a leitura seja feita da esquerda para à direita.

Propriedades numéricas

a) primeira coluna é formada pela progressão geométrica (potências de base 2) com termos duplicados: 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32 e que forma a base do triângulo numérico;

b) as sequências numéricas:

1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741 e

1, 3, 7, 17, 41, 99, 239, 577, 1393, 3363, 8119 também podem ser geradas pelo Algoritmo Escada de Theon;

c) o quociente 1,4142... da divisão 8119 / 5741 é a raiz quadrada aproximada de 2;

d) os números a partir da segunda coluna e depois dos números nas células azuis em suas mesmas colunas, são produtos de números da primeira coluna com números das células azuis;

Exemplos:

1 x 5 = 5

1 x 7 = 7

2 x 5 = 10

2 x 7 = 14

4 x 5 = 20

4 x 7 = 28

e assim sucessivamente.

Interessante observar que nas células azuis, os termos são constituídos por números ímpares e pares e, entre eles, números primos.

Triângulo numérico e extração da raiz quadrada de 3

a) primeira coluna é formada pela progressão geométrica (potências de base 3) com termos duplicados: 1, 1, 3, 3, 9, 9, 27, 27, 81, 81, 243, 243 e que forma a base do triângulo numérico;

b) as sequências numéricas nas células azuis, também podem ser geradas pelo Algoritmo Escada de Theon.

c) o quociente 1,732049037... da divisão 31648 / 18272 é a raiz quadrada aproximada de 3.

Interessante observar que nas células azuis, excluindo as potências de 3, os termos são constituídos por números pares.

Triângulo numérico e extração da raiz quadrada de 4

a) primeira coluna é formada pela progressão geométrica (potências de base 4) com termos duplicados: 1, 1, 4, 4, 16, 16, 64, 64, 256, 256, 1024, 1024 e que forma a base do triângulo numérico;

b) as sequências numéricas nas células azuis, também podem ser geradas pelo Algoritmo Escada de Theon.

c) o quociente 1,9999774... da divisão 88573 / 44287 é a raiz quadrada aproximada de 4.

Interessante observar que nas células azuis, os termos são constituídos por números ímpares e pares e, entre eles, números primos.

Triângulo numérico e extração da raiz quadrada de 5

a) primeira coluna é formada pela progressão geométrica (potências de base 5) com termos duplicados: 1, 1, 5, 5, 25, 25, 125, 125, 625, 625, 3125, 3125 e forma a base do triângulo numérico;

b) as sequências numéricas nas células azuis, também podem ser geradas pelo Algoritmo Escada de Theon.

c) o quociente 2,235955056... da divisão 203776 / 91136 é a raiz quadrada aproximada de 5.

Interessante observar que nas células azuis, excluindo as potências de 5, os termos são constituídos por números pares.

Triângulo numérico e extração da raiz quadrada de 6

Apresenta propriedades semelhantes do triângulo da raiz de 2.

Triângulo numérico e extração da raiz quadrada de 7

Apresenta propriedades semelhantes do triângulo da raiz de 3.

Triângulo numérico e extração da raiz quadrada de 8

Apresenta propriedades semelhantes do triângulo da raiz de 2.

Triângulo numérico e extração da raiz quadrada de 9

Apresenta propriedades semelhantes do triângulo da raiz de 2.

Triângulo numérico e extração da raiz quadrada de 10

Apresenta propriedades semelhantes do triângulo da raiz de 2.

Conclusão

A partir de progressões geométricas formadas por potências de números naturais a partir da base 2, com cada termo duplicado, se contrõem triângulos numéricos com os quais são possíveis de extrairem as raízes quadradas aproximadas das bases dessas potências.

Os triângulos numéricos formados por potências de bases ímpares apresentam, excluindo suas potências, as somas constituídas por números pares.

Os triângulos numéricos formados por potências de bases pares apresentam, excluindo suas potências, duas sequências cujas somas são constituídas por números pares e ímpares, e, entre eles, números primos.

Autor: Ricardo Silva - julho/2023

Fontes Bibliográficas:

[1] DENNIS, David and ADDINGTON, Susan. Square Root Calculations.http://quadrivium.info/MathInt/Notes/SquareRoots.pdf

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

005-texto-016-numeros-irracionais

011-estudos-443-numeros-triangulares-quadrados-perfeitos

011-estudos-444-numeros-triangulares-quadrados-produto-dois-numeros-consecutivos

011-estudos-446-numeros-triangulares-quadrados-perfeitos-e-o-numero-oito

011-estudos-448-escada-de-theon-ternos-pitagoricos-primitivos-raros

011-estudos-449-escada-de-theon-e-formulas-de-euclides

011-estudos-451-triangulos-numericos-arquitetos-medievais-extracao-de-raizes-quadradas

011-estudos-452-triangulo-fibonacci-auto-semelhante

Livro digital (e-book)

Números Primos e o

Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.