Página de estudos de matemática e sequências numéricas

Números Triangulares Quadrados e produto de 2 números consecutivos - 444

Números Triangulares Quadrados são números que ao mesmo tempo são números triangulares e quadrados perfeitos.

Há vários métodos de se gerarem números triangulares, um deles é por meio do produto de 2 números consecutivos tendo como resultado um número retangular e posteriormente dividindo por 2.

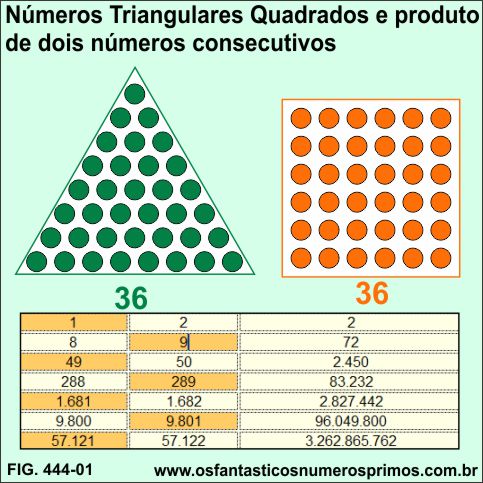
A metade de um número retangular é um número triangular.

O presente estudo demonstra interessantes regularidades numéricas entre determinados números consecutivos e seus produtos com a sequência de números triangulares quadrados.

Números consecutivos que são quadrados

A tabela a sequir apresenta os 15 primeiros números consecutivos cujos produtos são números retangulares.

As duplas de números que formam números consecutivos têm entre seus termos números quadrados perfeitos de forma alternada (células laranjas).

Números retangulares divididos por 2

A tabela a seguir apresenta os 15 primeiros determinados números retangulares que divididos por 2 têm como quocientes números triangulares quadrados.

Números triangulares quadrados e suas raízes quadradas

A tabela a seguir apresenta os 15 primeiros números triangulares quadrados e suas raízes quadradas.

Números consecutivos que são quadrados

Os dois números consecutivos cujos produtos são números retangulares e que geram números triangulares quadrados têm entre seus termos também números quadrados perfeitos (células laranjas).

Os números quadrados perfeitos têm seus algarismos finais terminados em 1 e 9 com as seguintes frequências:

a) coluna 1: 1, 9, 1, 1, 9, 1, 1;

b) coluna 2: 9, 9, 1, 9, 9, 1, 9.

Os números que não são quadrados terminam em 0, 2 e 8, com as seguintes frequências:

a) coluna 1: 8, 8, 0, 8, 8, 0, 8;

b) coluna 2: 2, 0, 2, 2, 0, 2, 2, 0

Consecutivo da coluna 1

Extraindo-se as raízes quadradas dos números da coluna 1 que são os primeiros termos das duplas de números consecutivos, constata-se que:

a) os primeiros termos e suas raízes quadradas exatas aparecem de forma alternada.

Efetuando-se as diferenças entre os números da coluna 1 que são os primeiros termos das duplas de números consecutivos, constata-se que:

a) a diferença entre um termo posterior e anterior é um número ímpar e, entre eles, números primos;

b) a diferença é também a raiz quadrada de um dos termos da coluna 1 (células coloridas).

Números consecutivo da coluna 2

Extraindo-se as raízes quadradas dos números da coluna 2 que são os segundos termos das duplas de números consecutivos, constata-se que:

a) os segundos termos e suas raízes quadradas exatas aparecem de forma alternada.

Efetuando-se as diferenças entre os números da coluna 2 que são os segundos termos das duplas de números consecutivos, constata-se que:

a) a diferença entre um termo posterior e anterior é um número ímpar e, entre eles, números primos;

A Escada de Theon de Smirna

"Theon de Smirna (viveu em torno de 140 E.C.) apresentou um algoritmo muito simples para calcular a raiz quadrada de 2, e que pode facilmente ser generalizado para achar a raiz quadrada de qualquer número natural. Em verdade, pode ser adaptado para achar qualquer raiz de números naturais." [1]

Fonte: adaptado de Tópicos de História da Matemática[1]

Construção da Escada de Theon

Pode se construir a Escada de Theon conforme etapas a seguir:

1) constrói-se uma tabela com duas colunas: (a) e (b);

coloca-se o número 1 na primeira linha, um abaixo de (a) e outro de (b).

2) soma-se 1(b) com 1(a) e coloca-se o resultado 2, abaixo de 1(a);

3) soma-se 1(a) com 2(a) e coloca-se o resultado 3, abaixo de 1(b);

4) soma-se 3(b) com 2(a) e coloca-se o resultado 5, abaixo de 2(b);

5) soma-se 2(a) com 5(b) e coloca-se o resultado 7, abaixo de 3(b);

6) soma-se 7(b) com 5(a) e coloca-se o resultado 12, abaixo de 5(b);

7) soma-se 5(a) com 12(a) e coloca-se o resultado 17, abaixo de 7(b);

e assim sucessivamente, somando-se dois números em uma mesma linha e somando-se dois últimos números da Coluna a.

Interessante observar que os termos da Coluna b do Algoritimo Escada de Theon são os mesmos que aparecem nas Tabela 5 e 6, ora como diferenças, ora como raízes quadradas.

Fórmula Algébrica da Escada de Theon

Por meio da seguinte fórmula, também pode-se construir o Algoritmo Escada de Theon.[2]

Com os termos iniciais:

a = 1

b = 1

i)

obtem-se 3 / 2

ii)

obtem-se 7 / 5

iii)

obtem-se 17 / 12

Fonte: adaptado de Tópicos de História da Matemática[1]

Autor: Ricardo Silva - junho/2023

Fontes Bibliográficas:

[1] PITOMBEIRA, João Bosco, ROQUE, Tatiana. Tópicos de História da Matemática. Edição Digital

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

[2] TANTON, James. On The Square Root of Two and Theon’s Ladder. www.jamestanton.com

https://en.wikipedia.org/wiki/Square_triangular_number

https://oeis.org/A001110

https://oeis.org/A001110/list

https://numbergenerator.org/numberlist

Matérias relacionadas:

011-estudos-004-soma-numeros-triangulares

011-estudos-015-numeros-triangulares-suas-posicoes-parte-1

011-estudos-025-numeros-triangulares-numeros-perfeitos

011-estudos-443-numeros-triangulares-quadrados-perfeitos

011-estudos-446-numeros-triangulares-quadrados-perfeitos-e-o-numero-oito

011-estudos-447-escada-de-theon-e-numeros-triangulares-quadrados-perfeitos

Livro digital (e-book)

Números Primos e o

Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.