


Theon de Smyrna (70 d. C. e 135 d. C) foi um filósofo e matemático grego, autor da obra “Matemáticas para entender Platão“ uma compilação introdutória da matemática grega. A obra do platônico inglês Thomas Taylor (1758-1835) “The Theoretic Arithmetic of the Pytagoreans“ divulgou amplamente o conhecimento deste livro na cultura ocidental. Um segundo trabalho sobre a ordem de estudo das obras de Platão foi descoberto em uma tradução árabe.[1][2].
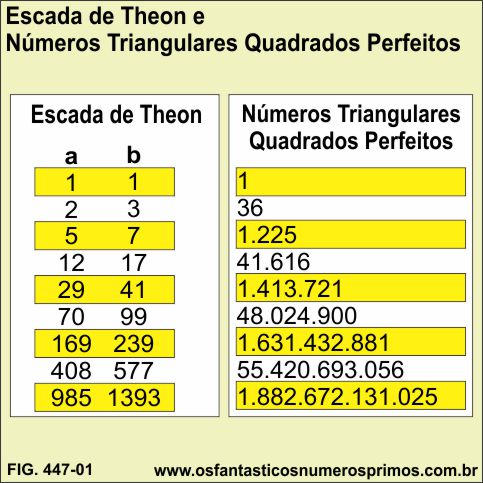
Theon de Smyrna também é autor de um dispositivo numérico, isto é, um algoritmo que leva o seu nome Escada de Theon com o qual é possível de se extrair a raiz quadrada de 2 (√2), como também ser adaptado para se extrair a raiz de qualquer número natural.
Dividindo-se os termos correspondentes b / a, o quociente tende a raiz quadrada de 2:
√2 = 1,4142
| Tabela 1 | |||
| Escada de Theon | |||
| sequência | sequência | ||
| ordem / | a | b | razão |
| posição | b / a | ||
| 1 | 1 | 1 | |
| 2 | 2 | 3 | 3 / 2 = 1,5 |
| 3 | 5 | 7 | 7 / 5 =1,4 |
| 4 | 12 | 17 | 17 / 12 = 1,41666... |
| 5 | 29 | 41 | 41 / 29 = 1,41379... |
| 6 | 70 | 99 | 99 / 70 = 1,41428... |
| 7 | 169 | 239 | 239 / 169 = 1,41420... |
Fonte: adaptado de Tópicos de História da Matemática[5]
O presente estudo demonstra outras propriedades e regularidades numéricas da Escada de Theon relacionadas a números retangulares, triangulares, bem como, a números triangulares quadrados perfeitos.
Na construção de seu algoritmo, Theon de Smyrna incia-se com um quadrado de lados 1 e estabelece a sua diagonal também em 1 unidade.[3]
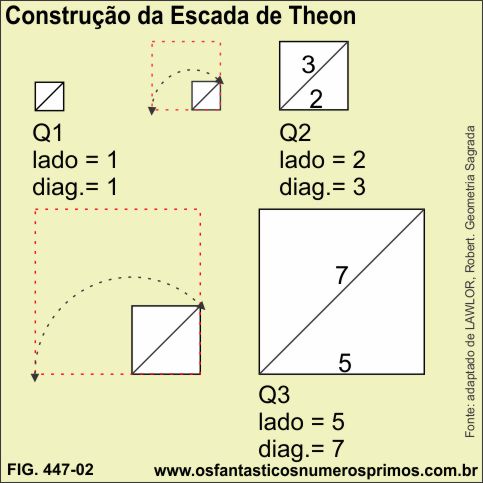
Fonte: adaptado Geometria Sagrada [3]
lado = 1
diagonal = 1
lado = 2 (soma do lado do quadrado 1 e diagonal 1 do quadrado 1).
diagonal = 3 (dobro do lado do quadrado 1 e diagonal 1 do quadrado 1).
lado = 5 (soma do lado do quadrado 2 e diagonal do quadrado 2).
diagonal = 7 (soma do dodro do lado do quadrado 2 e diagonal do quadrado 2).
Na Tabela 2, pode-se verificar as relações numéricas formadas a partir de um quadrado de lado 1 e diagonal de comprimento 1.
Na Tabela 2, observa-se também a afirmação de Theon, segundo a qual "o quadrado da diagonal sempre será o dobro do quadrado do lado, mas alternativamente maior ou menor em uma unidade".
| Tabela 2 | |||||
| lado do | quadrado | dobro | diagonal | quadrado | diferença |
| quadrado | do | quadrado | da | ||
| lado | diagonal | ||||
| 1 | 1 | 2 | 1 | 1 | 2 - 1 |
| 2 | 4 | 8 | 3 | 9 | 8 + 1 |
| 5 | 25 | 50 | 7 | 49 | 50 - 1 |
| 12 | 144 | 288 | 17 | 289 | 288 +1 |
| 29 | 841 | 1682 | 41 | 1681 | 1682 - 1 |
Fonte: adaptado de Geometria Sagrada
Pode-se construir a Escada de Theon conforme etapas a seguir:
1) constrói-se uma tabela com duas colunas: (a) e (b);
coloca-se o número 1 na primeira linha, um abaixo de (a) e outro de (b).
| a | b |
| 1 | 1 |
2) soma-se 1(b) com 1(a) e coloca-se o resultado 2, abaixo de 1(a);
| a | b |
| 1 | 1 |
| 2 |
3) soma-se 1(a) com 2(a) e coloca-se o resultado 3, abaixo de 1(b);
| a | b |
| 1 | 1 |
| 2 | 3 |
4) soma-se 3(b) com 2(a) e coloca-se o resultado 5, abaixo de 2(b);
| a | b |
| 1 | 1 |
| 2 | 3 |
| 5 |
5) soma-se 2(a) com 5(b) e coloca-se o resultado 7, abaixo de 3(b);
| a | b |
| 1 | 1 |
| 2 | 3 |
| 5 | 7 |
6) soma-se 7(b) com 5(a) e coloca-se o resultado 12, abaixo de 5(b);
| a | b |
| 1 | 1 |
| 2 | 3 |
| 5 | 7 |
| 12 |
7) soma-se 5(a) com 12(a) e coloca-se o resultado 17, abaixo de 7(b);
| a | b |
| 1 | 1 |
| 2 | 3 |
| 5 | 7 |
| 12 | 17 |
e assim sucessivamente, somando-se dois números em uma mesma linha e somando-se dois últimos números da Coluna a.
Pode-se construir a sequência (a) da Escada de Theon conforme etapas a seguir:
Incia-se a sequência com 1 e 2 e a partir do terceiro termo com o dobro do último número somado com o antepenúltimo.
| Tabela 3 | ||
| Escada de Theon (sequência a) | ||
| Método 3 | ||
| ordem / posição | a | |
| 1 | 1 | |
| 2 | 2 | |
| 3 | ( 2 x 2 ) + 1 | 5 |
| 4 | ( 2 x 5 ) + 2 | 12 |
| 5 | ( 2 x 12 ) + 5 | 29 |
| 6 | ( 2 x 29 ) + 12 | 70 |
| 7 | ( 2 x 70 ) + 29 | 169 |
| 8 | ( 2 x 169 ) + 70 | 408 |
| 9 | ( 2 x 408 ) + 169 | 985 |
| 10 | ( 2 x 985 ) + 408 | 2378 |
| 11 | ( 2 x 2378 ) + 985 | 5741 |
| 12 | ( 2 x 5741 ) + 2378 | 13860 |
| 13 | ( 2 x 13860 ) + 5741 | 33461 |
| 14 | ( 2 x 33461 ) + 13860 | 80782 |
| 15 | ( 2 x 80782 ) + 33461 | 195025 |
| www.osfantasticosnumerosprimos.com.br | ||
A metade dos termos da sequência (a) de ordens / posições pares da Escada de Theon têm como resultados as raízes quadradas de números triangulares quadrados perfeitos.
| Tabela 4 | |||
| Escada de Theon (sequência a) | |||
| ordem | a | raiz | Números |
| / posição | quadrada | Triangulares | |
| Quadrados | |||
| 1 | 1 | ||
| 2 | 2 | 1 | 1 |
| 3 | 5 | ||
| 4 | 12 | 6 | 36 |
| 5 | 29 | ||
| 6 | 70 | 35 | 1225 |
| 7 | 169 | ||
| 8 | 408 | 204 | 41616 |
| 9 | 985 | ||
| 10 | 2378 | 1189 | 1413721 |
| 11 | 5741 | ||
| 12 | 13860 | 6930 | 48024900 |
| 13 | 33461 | ||
| 14 | 80782 | 40391 | 1631432881 |
| 15 | 195025 | ||
| www.osfantasticosnumerosprimos.com.br | |||
Pode-se construir a sequência (b) da Escada de Theon conforme etapas a seguir:
Incia-se a sequência com 1 e 3 e a partir do terceiro termo com o dobro do último número somado com o antepenúltimo.
| Tabela 5 | ||
| Escada de Theon (sequência b) | ||
| Método 4 | ||
| ordem / | ||
| posição | b | |
| 1 | 1 | |
| 2 | 3 | |
| 3 | ( 2 x 3 ) + 1 | 7 |
| 4 | ( 2 x 7 ) + 3 | 17 |
| 5 | ( 2 x 17 ) + 7 | 41 |
| 6 | ( 2 x 41 ) + 17 | 99 |
| 7 | ( 2 x 99 ) + 41 | 239 |
| 8 | (2 x 239 ) + 99 | 577 |
| 9 | ( 2 x 577 ) + 239 | 1393 |
| 10 | ( 2 x 1393 ) + 577 | 3363 |
| 11 | ( 2 x 3363 ) + 1393 | 8119 |
| 12 | ( 2 x 8119 ) + 3363 | 19601 |
| 13 | ( 2 x 19601) + 8119 | 47321 |
| 14 | ( 2 x 47321 ) + 19601 | 114243 |
| 15 | ( 2 x 114243 ) + 47321 | 275807 |
| www.osfantasticosnumerosprimos.com.br | ||
A soma de 2 termos consecutivos da Sequência (b) da Escada de Theon tem como resultado o dobro de um termo da Sequência (a).
Exemplos:
1 + 3 = 4
3 + 7 = 10
7 + 17 = 24
| Tabela 6 | |||
| Escada de Theon (sequência b) | |||
| soma de 2 termos consecutivos | |||
| ordem / | soma | ||
| posição | a | b | (dobro de (a)) |
| 1 | 1 | 1 | |
| 2 | 2 | 3 | 4 |
| 3 | 5 | 7 | 10 |
| 4 | 12 | 17 | 24 |
| 5 | 29 | 41 | 58 |
| 6 | 70 | 99 | 140 |
| 7 | 169 | 239 | 338 |
| 8 | 408 | 577 | 816 |
| 9 | 985 | 1393 | 1970 |
| 10 | 2378 | 3363 | 4756 |
| 11 | 5741 | 8119 | 11482 |
| 12 | 13860 | 19601 | 27720 |
| 13 | 33461 | 47321 | 66922 |
| 14 | 80782 | 114243 | 161564 |
| 15 | 195025 | 275807 | 390050 |
| www.osfantasticosnumerosprimos.com.br | |||
Por meio da seguinte fórmula algébrica, também pode-se construir a Escada de Theon.[4]
| a + 2 x b |
| ----------- |
| a + b |
Com os termos iniciais:
a = 1
b = 1
i)
| 1 + 2 x 1 | 3 | |
| ----------- | = | ---- |
| 1 + 1 | 2 |
obtem-se 3 / 2
ii)
| 3 + 2 x 2 | 7 | |
| ----------- | = | ---- |
| 2 + 3 | 5 |
obtem-se 7 / 5
iii)
| 7 + 2 x 5 | 17 | |
| ----------- | = | ---- |
| 5 + 7 | 12 |
obtem-se 17 / 12
Determinados produtos de dois números consecutivos têm como resultados números retangulares que divididos por 2 geram números triangulares quadrados perfeitos.
Nas colunas: dobro do quadrado e quadrado da diagonal da Tabela 2, os números são os mesmos que aparecem na Tabela 3 - Produtos de 2 números consecutivos.
O Algoritmo Escada de Theon também geram números consecutivos que multiplicados geram números retangulares / oblongos e que divididos por 2 têm como quocientes números triangulares quadrados perfeitos.
| Tabela 7 | |||||
| lado | quadrado | dobro | diagonal | quadrado | diferença |
| do | do | do | |||
| quadrado | quadrado | diagonal | |||
| 1 | 1 | 2 | 1 | 1 | 2 - 1 |
| 2 | 4 | 8 | 3 | 9 | 8 + 1 |
| 5 | 25 | 50 | 7 | 49 | 50 - 1 |
| 12 | 144 | 288 | 17 | 289 | 288 +1 |
| 29 | 841 | 1682 | 41 | 1681 | 1682 - 1 |
Fonte: adaptado de Geometria Sagrada
| Tabela 8 | |||
| Produto de | |||
| 2 números consecutivos | |||
| números | |||
| consecutivos | produto | ||
| ordem / | coluna 1 | coluna 2 | número |
| posição | retangular | ||
| 1 | 1 | 2 | 2 |
| 2 | 8 | 9 | 72 |
| 3 | 49 | 50 | 2.450 |
| 4 | 288 | 289 | 83.232 |
| 5 | 1.681 | 1.682 | 2.827.442 |
| 6 | 9.800 | 9.801 | 96.049.800 |
| 7 | 57.121 | 57.122 | 3.262.865.762 |
| 8 | 332.928 | 332.929 | 110.841.386.112 |
| 9 | 1.940.449 | 1.940.450 | 3.765.344.262.050 |
| 10 | 11.309.768 | 11.309.769 | 12.791.086.352.3592 |
| 11 | 65.918.161 | 65.918.162 | 4.345.204.015.540.082 |
| 12 | 384.199.200 | 384.199.201 | 147.609.025.664.839.200 |
| 13 | 2.239.277.041 | 2.239.277.042 | 5.014.361.668.588.992.722 |
| 14 | 13.051.463.048 | 13051463049 | 170.340.687.706.360.913.352 |
| 15 | 76.069.501.249 | 76.069.501.250 | 5.786.569.020.347.682.061.250 |
| www.osfantasticosnumerosprimos.com.br | |||
A Tabela 4 apresenta as 15 primeiras duplas de termos da Escada de Theon e suas relações com números retangulares e números triangulares quadrados perfeitos.
| Tabela 9 | |||||
| Escada de Theon | |||||
| Números Triangulares Quadrados | |||||
| Escada de | |||||
| Theon | consecutivos | (produtos dos | (retangular / 2) | ||
| dobro | consecutivos) | ||||
| lado | diagonal | lado | quadrado | triangular | |
| quadrado | quadrado | diagonal | retangular | quadrado | |
| 1 | 1 | 2 | 1 | 2 | 1 |
| 2 | 3 | 8 | 9 | 72 | 36 |
| 5 | 7 | 50 | 49 | 2.450 | 1.225 |
| 12 | 17 | 288 | 289 | 83.232 | 41.616 |
| 29 | 41 | 1682 | 1681 | 2.827.442 | 1.413.721 |
| 70 | 99 | 9800 | 9801 | 96.049.800 | 48.024.900 |
| 169 | 239 | 57122 | 57121 | 3.262.865.762 | 1.631.432.881 |
| 408 | 577 | 332928 | 332929 | 110.841.386.112 | 55.420.693.056 |
| 985 | 1393 | 1940450 | 1940449 | 3.765.344.262.050 | 1.882.672.131.025 |
| 2378 | 3363 | 11309768 | 11309769 | 12.791.086.352.3592 | 63.955.431.761.796 |
| 5741 | 8119 | 65918162 | 65918161 | 4.345.204.015.540.082 | 2.172.602.007.770.041 |
| 13860 | 19601 | 384199200 | 384199201 | 147.609.025.664.839.200 | 73.804.512.832.419.600. |
| 33461 | 47321 | 2239277042 | 2239277041 | 5.014.361.668.588.992.722 | 2.507.180.834.294.496.361 |
| 80782 | 114243 | 13051463048 | 13051463049 | 170.340.687.706.360.913.352 | 85.170.343.853.180.456.676 |
| 195025 | 275807 | 76069501250 | 76069501249 | 5.786.569.020.347.682.061.250 | 2.893.284.510.173.841.030.625 |
| www.osfantasticosnumerosprimos.com.br | |||||
A Tabela 5 apresenta as 15 primeiras duplas de termos da Escada de Theon e seus produtos.
Os produtos de termos correspondentes da Escada de Theon têm como resultados as raízes quadradas de números triangulares quadrados perfeitos.
| Tabela 10 | ||||
| Escada de Theon | ||||
| e raízes quadradas de | ||||
| Números Triangulares Quadrados | ||||
| Escada de | ||||
| Theon | ||||
| lado | diagonal | produto | triangular | raiz |
| quadrado | quadrado | quadrada | ||
| 1 | 1 | 1 | 1 | 1 |
| 2 | 3 | 6 | 36 | 6 |
| 5 | 7 | 35 | 1.225 | 35 |
| 12 | 17 | 204 | 41.616 | 204 |
| 29 | 41 | 1189 | 1.413.721 | 1.189 |
| 70 | 99 | 6930 | 48.024.900 | 6.930 |
| 169 | 239 | 40391 | 1.631.432.881 | 40.391 |
| 408 | 577 | 235416 | 55.420.693.056 | 235.416 |
| 985 | 1393 | 1372105 | 1.882.672.131.025 | 1.372.105 |
| 2378 | 3363 | 7997214 | 63.955.431.761.796 | 7.997.214 |
| 5741 | 8119 | 46611179 | 2.172.602.007.770.041 | 46.611179 |
| 13860 | 19601 | 271669860 | 73.804.512.832.419.600. | 271.669.860 |
| 33461 | 47321 | 1583407981 | 2.507.180.834.294.496.361 | 1.583.407.981 |
| 80782 | 114243 | 9228778026 | 85.170.343.853.180.456.676 |
9.228.778.026 |
| 195025 | 275807 | 53789260175 | 2.893.284.510.173.841.030.625 | 53.789.260.175 |
| www.osfantasticosnumerosprimos.com.br | ||||
A Tabela 5 apresenta as 15 primeiras duplas de termos da Escada de Theon e suas respectivas ordens / posições.
| Tabela 11 | ||
| Escada de | ||
| Theon | ||
| ordem / | lado | diagonal |
| posição | quadrado | |
| a | b | |
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 5 | 7 |
| 4 | 12 | 17 |
| 5 | 29 | 41 |
| 6 | 70 | 99 |
| 7 | 169 | 239 |
| 8 | 408 | 577 |
| 9 | 985 | 1393 |
| 10 | 2378 | 3363 |
| 11 | 5741 | 8119 |
| 12 | 13860 | 19601 |
| 13 | 33461 | 47321 |
| 14 | 80782 | 114243 |
| 15 | 195025 | 275807 |
| www.osfantasticosnumerosprimos.com.br | ||
Efetuando-se a Divisão Euclidiana dos numeradores e denominadores de ordens pares das duplas de termos da Escada de Theon, os quocientes representam respectivamente as ordens dos números triangulares quadrados perfeitos, bem como, as raízes quadradas dos mesmos.[4]
a) Fração de posição 2
o primeiro triangular quadrado é 1.
1 é a raiz quadrada do triangular quadrado 1.
| 3 | 2 x (1) + 1 | |
| --- | = | ------------- |
| 2 | 2 x (1) + 0 |
b) Fração de posição 4
o oitavo triangular quadrado é 36.
6 é a raiz quadrada do triangular quadrado 36.
| 17 | 2 x (8) + 1 | |
| --- | = | -------------- |
| 12 | 2 x (6) + 0 |
c) Fração de posição 6
o quadragésimo nono triangular quadrado é 1225.
35 é a raiz quadrada do triangular quadrado 1225.
| 99 | 2 x (49) + 1 | |
| --- | = | ________ |
| 70 | 2 x (35) + 0 |
d) Fração de posição 8
o ducentésimo octagésimo oitavo triangular quadrado é 41616.
204 é a raiz quadrada do triangular quadrado 41616.
| 577 | 2 x (288) + 1 | |
| --- | = | ---------------- |
| 408 | 2 x (204) + 0 |
Autor: Ricardo Silva - julho/2023
[3]LAWLOR, Robert. Geometria Sagrada. Trad. Maria José Garcia Ripol: Edições del Prado, Madrid-Espanha, 1996
[5] PITOMBEIRA, João Bosco, ROQUE, Tatiana. Tópicos de História da Matemática. Edição Digital
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[4] TANTON, James. On The Square Root of Two and Theon’s Ladder. www.jamestanton.com
[1]https://es.wikipedia.org/wiki/
[2]https://www.matematicaparafilosofos.pt/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato