A Sequência de Fibonacci é formada repetindo-se o número 1 duas vezes e partir do terceiro termo somando-se dois termos anteriores:
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...)
1, 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
Ela aparece publicada no livro Liber Abaci (Livro de Cálculos) no ano de 1202, de autoria de Leonardo Fibonacci.
A Sequência de Fibonacci possui diversas propriedades, relacionadas a própria matemática, bem como, a geometria, a biologia, a física, a química, etc.
A sequência de Fibonacci tem aplicações na análise de mercados financeiros, na ciência da computação e na teoria dos jogos. Também aparece em configurações biológicas, como, por exemplo, na disposição dos galhos das árvores ou das folhas em uma haste, no arranjo do cone da alcachofra, do abacaxi, ou no desenrolar da samambaia.[1]
Johannes Kepler (1571-1630), astronômo, astrólogo e matemático alemão, em 1611, descobriu que dividindo um termo posterior com um termo anterior, o quociente tende ao número irracional 1,6180..., número este que mais tarde passou a ser chamado como: Número de Ouro, Número Áureo, Número Dourado, Número Ф (Fi).
François-Édouard-Anatole Lucas (1842-1891), matemático francês, foi quem observou que nos números dos problemas dos coelhos a partir do terceiro termo, somando-se dois termos anteriores, obtem-se o próximo termo e a partir dai passou a chamar como Sequência de Fibonacci.
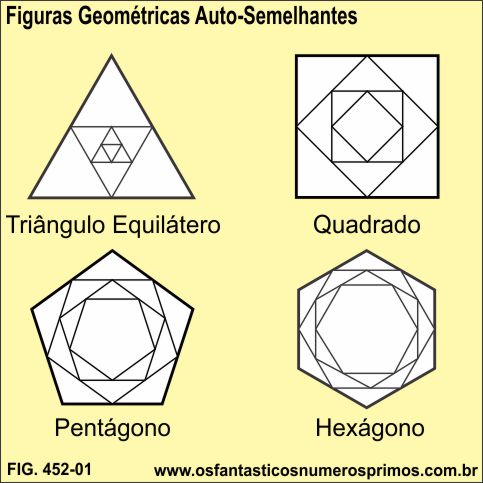
As figuras geométricas regulares possuem a propriedade de auto-semelhança, isto é, a partir do ponto médio de seus lados, e unindo-os com seguimentos de retas, podem ser construídas outras figuras semelhantes e proporcionais a original.
Nos exemplos a seguir, têm-se o triângulo equilátero, o quadrado, o pentágono e o hexágono, demonstrando a propriedade de auto-semelhança.
A estudante de arquitetura da Universidade da California - Los Angeles - UCLA - EUA, Sukuru Yuksel, pesquisando sobre como os arquitetos europeus do século X faziam para encontrar raízes quadradas, se deparou com o seguinte algoritmo: utilizando potências de base 2, com termos repetidos 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32 (coluna cor azul) e somando-os dois a dois, obtêm-se as somas dos mesmos. Dividindo os dois termos finais, obtêm-se a raiz quadrada aproximada de 2. [2]
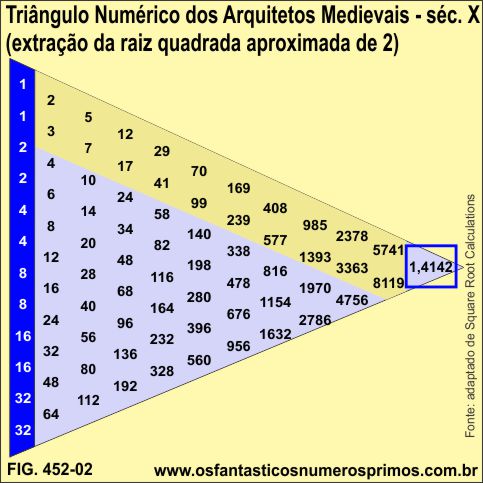
O triângulo apresenta os mesmos termos nas duas linhas paralelas a lateral esquerda o Algoritmo Escada de Theon:
1, 2, 5, 12, 29, 70,... e
1, 3, 7, 17, 41, 99,...
Além de gerar a raiz quadrada de 2, o triângulo apresenta diversas outras propriedades relacionadas a números triangulares, números quadrados perfeitos, números triangulares quadrados, bem como, com ternos pitagóricos raros e ternos pitagóricos derivados.
Para mais informações, veja matérias relacionadas abaixo.
Construindo-se um triângulo com números naturais, seguindo-se a estrutura do Triângulo dos Arquitetos Medievais adaptado, observa-se que:
a) números quadrados perfeitos ficam alinhados horizontalmente;
b) nas primeiras 2 colunas, há ocorrências de números ímpares;
c) a partir da coluna 3, os demais números são pares.
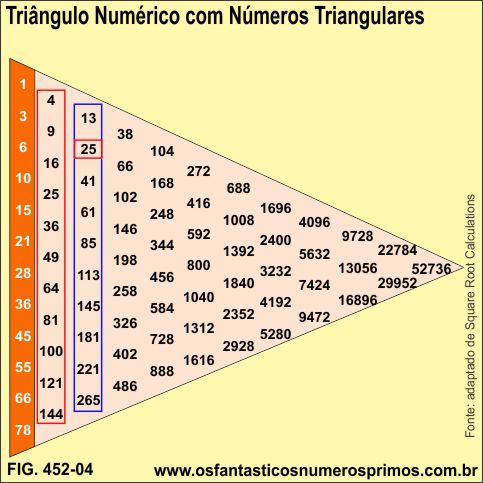
Construindo-se um triângulo com números triangulares, seguindo-se a estrutura do Triângulo dos Arquitetos Medievais adaptado, observa-se que:
a) números quadrados perfeitos ficam alinhados verticalmente na segunda coluna;
b) nas primeiras 3 colunas há ocorrências de números ímpares;
c) a partir da coluna 4, os demais números são pares.
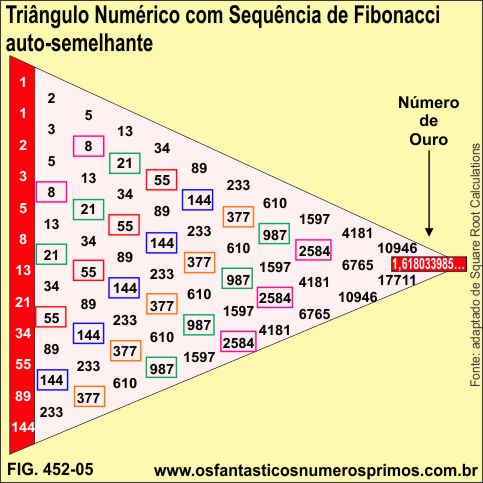
Construindo-se um triângulo com Números de Fibonacci e seguindo-se a estrutura do Triângulo dos Arquitetos Medievais adaptado, observa-se uma outra interessantíssima propriedade relacionada aos Números de Fibonacci de que: Os números de Fibonacci geram os próprios Números de Fibonacci por meia da soma de duplas de números de Fibonacci.
Interessante observar que as colunas inciam-se com termos da Sequência de Fibonacci cujas ordens / posições são ímpares ímpares.
Olhando em sentindo horizontal, os números ímpares estão alinhados com números ímpares e números pares com números pares.
Em sentido oblíquo, da direita superior para à esquerda inferior, ou vice-versa, os Números de Fibonacci são os mesmos (retângulos coloridos).
Acompanhando a lateral esquerda do triângulo, de forma intercalada, os Números de Fibonacci são termos de ordens / posições ímpares ora pares.
Observação muito importante: nos estudos publicados aqui no WebSite Os Fantásticos Números Primos, bem como, na coleção de livros digitais de sequências numéricas aqui divulgados, é a primeira vez que um fato matemático dessa natureza acontece, isto é, uma sequência numérica que gera termos sequênciais de sua própria sequência numérica.
Autor: Ricardo Silva - julho/2023
[2] DENNIS, David and ADDINGTON, Susan. Square Root Calculations.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1]https://pt.wikipedia.org
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
