


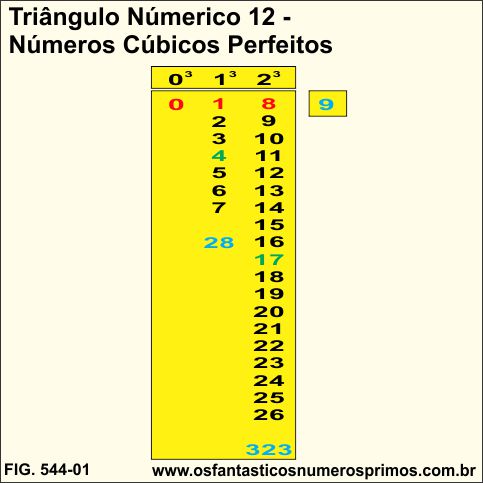
Triângulo Numérico 12 - Números Cúbicos Perfeitos é um dispositivo numérico infinito no qual números naturais cúbicos perfeitos iniciam cada uma das colunas ou linhas formando um triângulo.
A disposição de números naturais em formato de triângulo iniciando com números cúbicos até um número quase-cubo perfeito apresenta interessantes propriedades numéricas e algébricas relacionadas com a sequência de números quadrados perfeitos, número triangulares e números hexagonais centrados.
O presente estudo demonstram métodos e novas fórmulas nos quais são possíveis de se determinar termos principais, bem como, a soma de progressão aritmética finita em que o primeiro termo é um número cúbico perfeito, o último termo é um número quase-cúbico perfeito e razão 1 unidade.
Número cúbico perfeito é um número natural que é produto por ele mesmo três vezes.
Exemplos:
0 x 0 x 0 = 0
1 x 1 x 1 = 1
2 x 2 x 2 = 8
3 x 3 x 3 = 27
Para indicar uma multiplicação em que os fatores são iguais, usamos a Potenciação.
Exemplos:
03 = 0
13 = 1
23 = 8
33 = 27
Números cúbicos perfeitos também podem ser gerados:
a) da soma de sequências de números ímpares;
Exemplo 1)
1 = 1
Exemplo 2)
3 + 5 = 8
Exemplo 3)
7 + 9 + 11 = 27
b) do quadrado da soma de números consecutivos cujo resultado é a soma dos cubos de suas parcelas.
Exemplo 1)
( 1 + 2 )2 = 13 + 23
32 = 1 + 8
9 = 9
Exemplo 2)
( 1 + 2 + 3 )2 = 13 + 23+ 33
62 = 1 + 8 + 27
36 = 36
c) elevando-se os termos do Terno Pitagórico 3-4-5, bem como, seus ternos derivados ao cubo e somando-os, obtem-se também um número cúbico.
a3 + b3 + c3 = d3
53 + 43 + 33 = 63
125 + 64 + 27 = 216
d) de número cúbico somado com o produto de 6 por um triangular somado 1 unidade.
Observação: o número base do cubo é a ordem / posição do triangular que é multiplicado por 6.
Exemplo 1)
13 + ( 6 x 1 + 1 )
1 + 7 = 8
1 é o primeiro triangular.
Exemplo 2)
23 + ( 6 x 3 + 1 )
8 + 19 = 27
3 é segundo triangular.
Exemplo 3)
33 + ( 6 x 6 + 1 )
27 + 37 = 64
6 é o terceiro triangular.
O Triângulo Numérico 12 - Números Cúbicos Pefeitos apresenta as seguintes propriedades:
a) a primeira linha do triângulo e formada por números cúbicos perfeitos;
b) cada sequência numérica tem como primeiro termo um número cúbido perfeito e último termo um número quase-cubo perfeito, isto é, um número antecessor de um número cúbico perfeito.
c) a soma de números cúbicos perfeitos consecutivos têm como resultado um número quadrado perfeito cuja raiz quadrada é um número triangular;
Exemplo 1)
0 + 1 = 1
√1 = 1
1 é um número triangular.
Exemplo 2)
0 + 1 + 8 = 9
√9 = 3
3 é um número triangular.
Exemplo 3)
0 + 1 + 8 + 27 = 36
√36 = 6
6 é um número triangular e perfeito
Exemplo 4)
0 + 1 + 8 + 27 + 64 = 100
√100 = 10
10 é um número triangular.
d) o triplo de uma raiz cúbica multiplicada por esta raiz cúbica somada 1 unidade tem como resultado a quantidade de termos após o número cúbico da respectiva raiz.;
| 3 x 3 √B ( 3 √B + 1 ) |
Exemplo 1)
3 x 3√1 x ( 3√1 + 1) =
= 3 x 1 x ( 1 + 1)
= 3 x 2
= 6
Após o cubo 1, há 6 termos.
Exemplo 2)
3 x 3√8 x ( 3√8 + 1) =
= 3 x 2 x ( 2 + 1)
= 6 x 3
= 18
Após o cubo 8, há 18 termos.
e) o triplo de uma raiz cúbica multiplicada por esta raiz cúbica somada 1 unidade e posteriormente somada 1 unidade tem como resultado a quantidade de termos da sequência que se inicia com um número cúbico e termina com um número quase-cubo perfeito, isto é, um número que é antecessor de um número cúbico perfeito.;
| [ 3 x 3 √B ( 3 √B + 1 ) ] + 1 |
Exemplo 1)
[ 3 x 3√1 x ( 3√1 + 1) ] + 1 =
= [ 3 x 1 x ( 1 + 1) ] + 1
= [ 3 x 2 ] + 1
= 7
O resultado 7 também é a diferença entre os cubos 8 e 1
8 - 1 = 7
7 é um número hexagonal centrado.
Exemplo 2)
[ 3 x 3√8 x ( 3√8 + 1) ] + 1
= [ 3 x 2 x ( 2 + 1) ] + 1
= [ 6 x 3 ] + 1
= 19
O resultado 19 também é a diferença entre os cubos 27 e 8
27 - 8 = 19
19 é um número hexagonal centrado.
f) um número cúbico mais a metade do triplo de sua raiz cúbica multiplicada por sua raiz cúbica somada 1 unidade tem como resultado o termo médio da sequência que se inicia com um número cúbico e termina com um número quase-cubo perfeito, isto é, um número que é antecessor de um número cúbico perfeito.;
| B + 1/2 ( 3 x 3 √B ( 3 √B + 1) ) |
Exemplo 1)
13 + [ 1/2 x { (3 x 3√1) x ( 3√1 + 1) }] =
= 1 + [ 1/2 { (3 x 1) x ( 1 + 1) } ]
= 1 + [ 1/2 { 3 x 2 } ]
= 1 + [ 1/2 { 6 } ]
= 1 + [ 3 ]
= 1 + 3
= 4
Exemplo 2)
23 + [ 1/2 x { (3 x 3√8) x ( 3√8 + 1) } ] =
= 8 + [ 1/2 { (3 x 2) x ( 2 + 1) } ]
= 8 + [ 1/2 { 6 x 3 } ]
= 8 + [ 1/2 { 18 } ]
= 8 + [ 9 ]
= 17
Outra fórmula variante de se gerar o termo médio da sequência que se inicia com um número cúbico e termina com um número quase-cubo perfeito é:
| n3 + 3n( n + 1 ) / 2 |
Exemplo 1)
n3 + 3n ( n + 1 ) / 2 =
= 13 + 3.1( 1 + 1 ) / 2
= 1 + 3 ( 2 ) / 2
= 1 + 6 / 2
= 1 + 3
= 4
g) um número cúbico mais o triplo de sua raiz cúbica multiplicada por sua raiz cúbica somada 1 unidade tem como resultado o último termo da sequência que se inicia com um número cúbico e termina com um número quase-cubo perfeito, isto é, um número que é antecessor de um número cúbico perfeito.;
| B + 3 x 3 √B ( 3 √B + 1 ) |
Exemplo 1)
1 + [ 3 x 3√1 x ( 3√1 + 1) ] =
= 1 + [ 3 x 2 ]
= 1 + 6
= 7
Exemplo 2)
8 + [ 3 x 3√8 x ( 3√8 + 1) ] =
= 1 + [ 6 x 3 ]
= 1 + 18
= 19
h) um número cúbico mais a metade do triplo de sua raiz cúbica multiplicada por sua raiz cúbica somada 1 unidade multiplicado por esse mesmo número cúbico mais o triplo de sua raiz cúbica multiplicada por sua raiz cúbica somada 1 unidade tem como resultado a soma dos termos da sequência que se inicia com um número cúbico e termina com um número quase-cubo perfeito, isto é, um número que é antecessor de um número cúbico perfeito.;
| ( B + 1/2 ( 3 3 √B ( 3 √B + 1) ) x ( 3 3 √B ( 3 √B + 1 ) |
Exemplo 1)
13 + [ 1/2 x { (3 x 3√1) x ( 3√1 + 1) } ] x [ 1 + { 3 x 3√1 x ( 3√1 + 1) } ] =
4 x 7 = 28 (produto do termo médio pelo último termo)
Exemplo 1)
23 + [ 1/2 x { (3 x 3√8) x ( 3√8 + 1) } ] x [ 1 + { 3 x 3√8 x ( 3√8 + 1) } ] =
17 x 19 = 323 (produto do termo médio pelo último termo)
| Triângulo Numérico 12 | ||||||
| Números Cúbicos Perfeitos | ||||||
| 03 | 13 | 23 | 33 | 43 | ||
| soma | ||||||
| cubos | ||||||
| Cubos Perfeitos | 0 | 1 | 8 | 27 | 64 | 100 |
| 2 | 9 | 28 | 65 | |||
| 3 | 10 | 29 | 66 | |||
| 4 | 11 | 30 | 67 | |||
| 5 | 12 | 31 | 68 | |||
| 6 | 13 | 32 | 69 | |||
| 7 | 14 | 33 | 70 | |||
| 15 | 34 | 71 | ||||
| soma | 28 | 16 | 35 | 72 | ||
| 17 | 36 | 73 | ||||
| 18 | 37 | 74 | ||||
| 19 | 38 | 75 | ||||
| 20 | 39 | 76 | ||||
| 21 | 40 | 77 | ||||
| 22 | 41 | 78 | ||||
| 23 | 42 | 79 | ||||
| 24 | 43 | 80 | ||||
| 25 | 44 | 81 | ||||
| 26 | 45 | 82 | ||||
| 46 | 83 | |||||
| soma | 323 | 47 | 84 | |||
| 48 | 85 | |||||
| 49 | 86 | |||||
| 50 | 87 | |||||
| 51 | 88 | |||||
| 52 | 89 | |||||
| 53 | 90 | |||||
| 54 | 91 | |||||
| 55 | 92 | |||||
| 56 | 93 | |||||
| 57 | 94 | |||||
| 58 | 95 | |||||
| 59 | 96 | |||||
| 60 | 97 | |||||
| 61 | 98 | |||||
| 62 | 99 | |||||
| 63 | 100 | |||||
| 101 | ||||||
| soma | 1665 | 102 | ||||
| 103 | ||||||
| 104 | ||||||
| 105 | ||||||
| 106 | ||||||
| 107 | ||||||
| 108 | ||||||
| 109 | ||||||
| 110 | ||||||
| 111 | ||||||
| 112 | ||||||
| 113 | ||||||
| 114 | ||||||
| 115 | ||||||
| 116 | ||||||
| 117 | ||||||
| 118 | ||||||
| 119 | ||||||
| 120 | ||||||
| 121 | ||||||
| 122 | ||||||
| 123 | ||||||
| 124 | ||||||
| soma | 5734 | |||||
Fonte: adaptado de MARQUES, David Dias. 003 - Organização de Números Cúbicos (∆seq3) - (Triângulo Numérico 12 - Números Cúbicos Perfeitos). Paracuru - CE, 2025.
Autor: Ricardo Silva - Fevereiro/2025
MARQUES, David Dias Marques. 003 - Organização de Números Cúbicos (∆seq3) - (Triângulo Numérico 12 - Números Cúbicos Perfeitos). Paracuru - CE, 2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato