Página de estudos de matemática e sequências numéricas

Soma de 3 Números Cúbicos Consecutivos - 602

Número Cúbico Perfeito é um número que é produto de um natural multiplicado por esse número 3 vezes:

3 x 3 x 3 = 27

ou também por meio da Potênciação, elevando-se a número (base) ao expoente 3:

3³= 3 x 3 x 3 x = 27

O presente estudo demonstra relações numéricas entre soma de 3 números cúbicos consecutivos com múltiplos de 3, seus fatores, bem como, com a sequência de números retangulares.

A partir do segundo fator de uma multiplicação e de um múltiplo de 3 é possível de se determinar um número retangular e assim gerar 3 números cúbicos consecutivos, bem como, a soma desses mesmos números cúbicos.

O estudo demonstra também a Fórmula Variante S3CC-II - Soma de 3 Números Consecutivos-II.

Soma de 3 Números Consecutivos

A Tabela-1 apresenta as 27 primeiras somas de 3 números consecutivos.

A soma de 3 números consecutivos têm como resultados múltiplos de 3 a partir do número 6.

A soma de 3 números consecutivos dividido por 3 têm como resultado o termo médio dos 3 números consecutivos, isto é, a média aritmética.

Soma de 3 Números Cúbicos Consecutivos

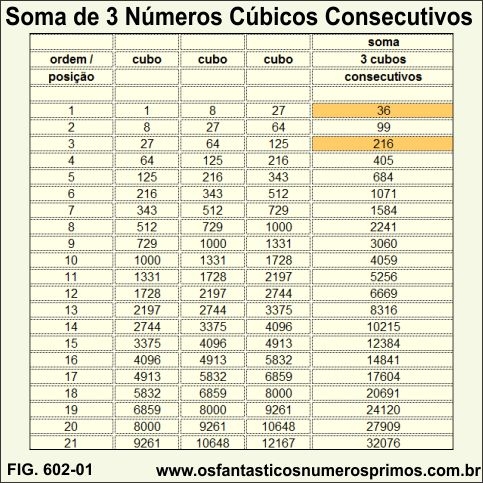
A Tabela-2 apresenta as 27 primeiras somas de 3 números cúbicos consecutivos.

As somas de 3 números consecutivos não formam uma sequência numérica famosa, mas entre seus termos, há ocorrências raras de alguns números famosos, tais como 36 (quadrado) , 216 (cubo) , 41616 (quadrado), destacados em laranja.

As somas de 3 números cúbicos consecutivos têm como resultados números múltiplos de 3.

Soma de 3 Cubos Consecutivos e Soma de 3 Números Consecutivos

A somas de 3 números cúbicos consecutivos divididas pelas somas de 3 números consecutivos correspondentes têm como quocientes números que são múltiplos de 3 e números que não são múltiplos de 3.

Exemplos de números não múltiplos de 3:

11, 38, 83, 146, ... (células laranja).

Interessante observar que os números (quocientes) que não são múltiplos de 3, são de ordens / posições que também não são múltiplos de 3.

Diferença entre Quociente e Soma de 3 Números Consecutivos

A diferença entre o quociente da soma de 3 cubos consecutivos e a soma de 3 números consecutivos tem como resultado a sequência de números retangulares.

Observação 0 (zero) não é um número retangular.

De onde de deduz a Fórmula Variante S3CC-II:

O produto de um múltiplo de 3 pelo mesmo múltiplo de 3 somado com um número retangular tem como resultado a soma de 3 números cúbicos consecutivos.

Exemplos:

a) para n = 1

i) [ 3 { ( n ( n + 1 ) ) + 1 } ] . [ [ 3 { ( n (n + 1) ) + 1} ] + [ { n . (n + 1) } ] ]

ii) [ 3 { ( 1 ( 1 + 1 ) ) + 1 } ] . [ [ 3 { (1 ( 1 + 1) ) + 1} ] + [ { 1 . ( 1 + 1) } ] ]

iii) [ 3 { ( 2 ) + 1 } ] . [ [ 3 { ( 2 ) + 1} ] + [ { 1 . ( 2 ) } ] ] ]

iv) [ 3 . 3 ] . [ [ 3 . 3 ] + 2 ] ]

v) 9 x [ 9 + 2 ] = 9 x 11 = 99

Observações: n = 1

3 x 3 = 9

o segundo fator 3 é 2 unidades maior que n=1

b) 12 x [ 12 + 6 ] = 12 x 18 = 216

Observações: n = 2

3 x 4 = 12

o segundo fator 4 é 2 unidades maior que n=2

c) 15 x [ 15 + 12 ] = 15 x 27 = 405

Observações: n = 3

3 x 5 = 15

o segundo fator 5 é 2 unidades maior que n=3

Calculando cubos e somas de 3 cubos consecutivos

1) Sabendo que a multiplicação de 3 x 6 = 18, calcular os 3 cubos consecutivos, bem como, sua soma.

a) subtraia 2 unidade do segundo fator 6;

6 - 2 = 4

b) na fórmula de números retangulares, substitui-se n por 4;

i) n x ( n + 1)

ii) 4 x ( 4 + 1)

iii) 4 x 5 = 20 (número retangular)

c) soma de 3 cubos consecutivos

18 x ( 18 + 20 ) = 18 x 38 = 684

d) calculando os cubos

2) Sabendo que a multiplicação de 3 x 7 = 21, calcular os 3 cubos consecutivos, bem como, sua soma.

a) subtraia 2 unidade do segundo fator 7;

7 - 2 = 5

b) na fórmula de números retangulares, substitui-se n por 5;

i) n x ( n + 1)

ii) 5 x ( 5 + 1)

iii) 5 x 6 = 30 (número retangular)

c) soma de 3 cubos consecutivos

21 x ( 21 + 30 ) = 21 x 51 = 1071

d) calculando os cubos

Autor: Ricardo Silva - setembro/2025

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

ari-costa-2025-007-formula-variante-soma-3-cubos-consecutivos

011-estudos-150-numeros-triangulares-quadrados-cubicos

011-estudos-239-numeros-cubicos-e-sequencias-numericas

011-estudos-268-tabuada-numeros-cubicos

011-estudos-540-tricubo-pitagorico-e-numeros-cubicos

011-estudos-541-500-primeiros-ternos-pitagoricos-primitivos-ao-cubo

Livro digital (e-book)

Escada de Theon

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Primos e o

Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.