


Fez-se a seguinte pesquisa ao Navegador Google, na data de 20/12/2025: Dada a hipotenusa, como calcular os catetos ?
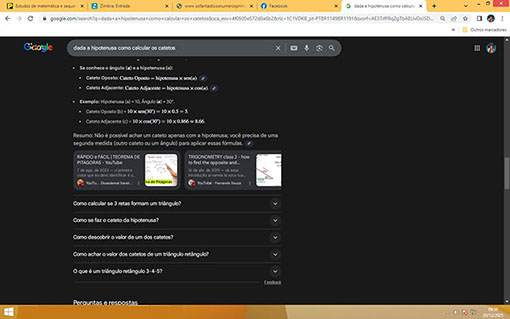
Entre vários resultados, aparece a seguinte resposta:
"Resumo: Não é possível achar um cateto apenas com a hipotenusa; você precisa de uma segunda medida (outro cateto ou ângulo) para aplicar essas fórmulas."
Estudos divulgados aqui no WebSite, bem como, na coleção de livros Os Fantásticos Números Primos, demonstram que a partir de um número ímpar igual ou maior que 3, bem como, de um quadrado perfeito igual ou maior que 9 são possíveis de gerarem ternos pitagóricos primitivos, grupos de 3 números inteiros que são medidas dos lados de triângulo retângulo escaleno: cateto menor, cateto maior e hipotenusa.
Veja abaixo, para mais informações, Matérias Relacionadas !
Pierre de Fermat, jurista e Entusiasta Matemático francês, (1601-1665), entre várias contribuições à Matemática, em carta a Marin Mersenne (1588-1648), datada de 25 de dezembro de 1640, afirma que números primos da forma 4x + 1 podem ser escritos como soma de 2 quadrados enquanto números da forma 4x + 3 não podem ser escritos como a soma de 2 quadrados.[1]

Partindo se da descoberta de Pierre de Fermat e estudando as propriedades de números da forma 4x + 1 são possíveis sim, de se obterem medidas do cateto menor e do cateto maior a partir da medida da hipotenusa, sem fazer uso do Teorema de Pitágoras e de Cálculos Trigonométricos a partir de alguns cálculos dos algoritmos S2Q-1 (Soma de 2 Quadrados - 1) e S2Q2 (Soma de 2 Quadrados - 2).
Veja abaixo, para mais informações, Matérias Relacionadas !
Números de Fermat da forma 4x + 1, onde x é um número triangular possuem propriedades e relações numéricas com os próprios números triangulares e a sequência de números retangulares.
O número 5 é um número da forma 4x + 1, pois:
4 x 1 (triangular) + 1 = 5
i) escreve-se o número 5 como soma de 2 números consecutivos;
(5 - 1) / 2 = 2
(5 + 1) / 2 = 3
2 + 3 = 5
ii) a primeira parcela 2 é um número retangular;
iii) número retangular é produto de 2 números consecutivos;
1 x 2 = 2
iv) somam-se os fatores 1 e 2;
1 + 2 = 3
v) subtrái-se 1 unidade da hipotenusa 5;
5 - 1 = 4
Terno Pitagórico Primitivo de Ordem Triangular 3-4-5
Cateto Menor = 3
Cateto Maior = 4
Hipotenusa = 5
O número 13 é um número da forma 4x + 1, pois:
4 x 3 (triangular) + 1 = 13
i) escreve-se o número 13 como soma de 2 números consecutivos;
(13 - 1) / 2 = 6
(13 + 1) / 2 = 7
6 + 7 = 13
ii) a primeira parcela 6 é um número retangular;
iii) número retangular é produto de 2 números consecutivos;
2 x 3 = 6
iv) somam-se os fatores 2 e 3;
2 + 3 = 5
v) subtrái-se 1 unidade da hipotenusa 13;
13 - 1 = 12
Terno Pitagórico Primitivo de Ordem Triangular 5-12-13
Cateto Menor = 5
Cateto Maior = 12
Hipotenusa = 13
O número 25 é um número da forma 4x + 1, pois:
4 x 6 (triangular) + 1 = 25
i) escreve-se o número 25 como soma de 2 números consecutivos;
(25 - 1) / 2 = 12
(25 + 1) / 2 = 13
12 + 13 = 25
ii) a primeira parcela 12 é um número retangular;
iii) número retangular é produto de 2 números consecutivos;
3 x 4 = 12
iv) somam-se os fatores 3 e 4;
3 + 4 = 7
v) subtrái-se 1 unidade da hipotenusa 25;
25 - 1 = 24
Terno Pitagórico Primitivo de Ordem Triangular 7-24-25
Cateto Menor = 7
Cateto Maior = 24
Hipotenusa = 25
Autor: Ricardo Silva - dezembro/2025
[1] NETO, Angelo Papa. Soma de 2 quadrados. IFCE
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato