


Assim como o Teorema de Pitágoras tem vasta aplicação em vários ramos das Ciências, a Equação do Segundo Grau não foge à regra, pois também é utilizada em diversas áreas para resoluções de problemas matemáticos, possui várias propriedades, sua estrutura pode ser completa e incompleta, isto é, pode ter de um a três termos e ainda pode ser resolvida por diversos métodos com a utilização da Geometria, Álgebra ou Álgebra e Geometria conjuntamente.
Por muito tempo, ficava imaginando como surgiu a Equação do Segundo Grau, como a inventaram.
Imagine você há centenas de anos atrás, na região da Mesopotânia, brincando talvez com um Quebra-Cabeça cujas peças são quadradinhos como das figuras a seguir.
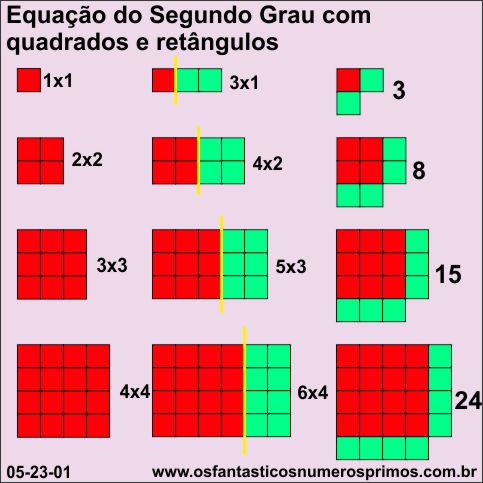
Você começa a montar figuras de quadrados e retângulos da seguinte forma:
a) monta-se um quadrado (1x1) - uma peça;
b) acrescenta-se peças com o dobro do lado do quadrado formando retângulo;
c) e na terceira etapa monta-se uma figura tipo "cantoneira" com a quantidade de peças do retângulo, deslocando uma das coluna de quadrados para a base do quadrado.
O objetivo é ir montando, quadrados, retângulos e cantoneiras.
Padrões tanto geométricos quanto numéricos nas montagens da figuras vão surgindo.
A justaposição de quadradinhos formam-se números figurados.
Em relação aos padrões numéricos, tem-se sequência de números quadrados perfeitos, sequência de números oblongos (números retangulares) e uma outra sequência em que os números são uma unidade menor que um número quadrado perfeito (números quase quadrados perfeitos).
Estes padrões, como veremos a seguir, podem ter sido as bases de concepção da Equação do Segundo Grau.
The Story of Maths - The Language of The Universe
Escrito e apresentado pelo Prof. Marcus Du Sautoy.
The Open University - BBC - XXVIII.
Na cena do filme, no tempo de 30 mim e 04 segundos é apresentado como a civilização da Babilônia resolvia Equação Quadrática, isto é, Equação do Segundo Grau a partir da área de um terreno.
No exemplo, a partir de uma área de 55 unidades quadradas, com o lado maior somando 6 unidades a mais que o lado menor, quanto mede o lado menor?

A solução apresentada no filme é a utilização do Método de Completar Quadrados.
x (x + 6) = 55
x2 + 6x = 55
dividi-se o coeficiente 6 do termo "bx" por 2 e eleve ao quadrado e some-o ao primeiro e segundo membros para equilibrar a equação.
x2 + 6x + 32 = 55 + 32
x2 + 6x + 9 = 55 + 9
o primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 6x + 9 = 64
fatora-se o primeiro membro - quadrado da soma (produto notável).
(x + 3)2 = 64
extrai-se a raiz quadrada dos dois membros.
x + 3 = ± √64
x + 3 = ± 8
Solução positiva
x' = + 8 - 3 = 5
Solução negativa
x" = - 8 - 3 = -11
Resolver uma Equação do Segundo Grau é encontrar dois números cuja soma e produtos são conhecidos.
Nos exemplos abaixo, precisam se saber quais são as incógnitas que somadas duas vezes o lado de um quadrado tem como resultado a área de um retângulo
ou
tendo um retângulo formado por tantas unidades quadradas, quais os números que formam o seu maior e menor lados (largura e altura).
A soma é 4 e o produto é 3.
Através da adição, o número 4 pode ser obtido:
1 + 3 = 4
2 + 2 = 4
Através da multiplicação o número 3 pode ser obtido:
1 x 3 = 3
O semiperímetro do retângulo é 4 (largura 3 + altura 1).

A Equação do Segundo Grau não é um trinômio quadrado perfeito.
x (x+2) = 3
x2 + 2x = 3
dividi-se o coeficiente 2 do termo "bx" por 2 e eleve ao quadrado e some-o ao segundo membro para equilibrar a equação.
x2 + 2x + 12 = 3 + 12
x2 + 2x + 1 = 3 + 1
o primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 2x + 1 = 3 + 1
fatora-se o primeiro membro - quadrado da soma (produto notável).
(x + 1)2 = 4
extrai-se a raiz quadrada dos dois membros.
x + 1 = ± √4
x + 1 = ± 2
Solução positiva
x' = + 2 - 1 = 1
Solução negativa
x" = - 2 - 1 = - 3
A soma é 6 e o produto é 8.
Através da adição, o número 6 pode ser obtido:
1 + 5 = 6
2 + 4 = 6
3 + 3 = 6
Através da multiplicação o número 8 pode ser obtido:
1 x 8 = 8
2 x 4 = 8
O semiperímetro do retângulo é 6 (largura 4 + altura 2).
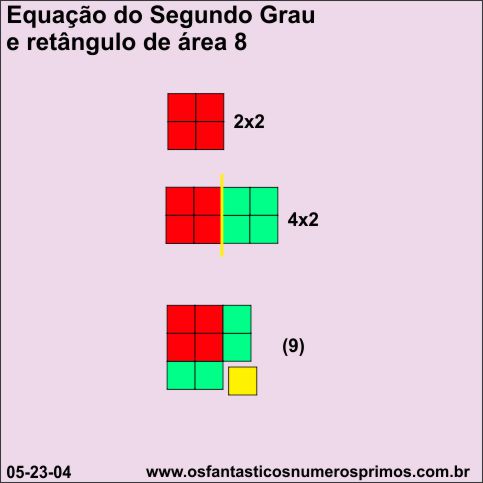
A Equação do Segundo Grau não é um trinômio quadrado perfeito.
x (x+2) = 8
x2 + 2x = 8
dividide-se o coeficiente 2 do termo "bx" por 2 e eleve ao quadrado e some-o ao primeiro e segundo membros para equilibrar a equação.
x2 + 2x + 12 = 8 + 12
x2 + 2x + 1 = 8 + 1
o primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 2x + 1 = 9
fatora-se o primeiro membro - quadrado da soma (produto notável).
(x + 1)2 = 9
extrai-se a raiz quadrada dos dois membros.
x + 1 = ± √9
x + 1 = ± 3
Solução positiva
x' = + 3 - 1 = 2
Solução negativa
x" = - 3 - 1 = - 4
A soma é 8 e o produto é 15.
Através da adição, o número 8 pode ser obtido:
1 + 7 = 8
2 + 6 = 8
3 + 5 = 8
4 + 4 = 8
Através da multiplicação o número 15 pode ser obtido:
1 x 15 = 15
3 x 5 = 15
O semiperímetro do retângulo é 8 (largura 5 + altura 3).
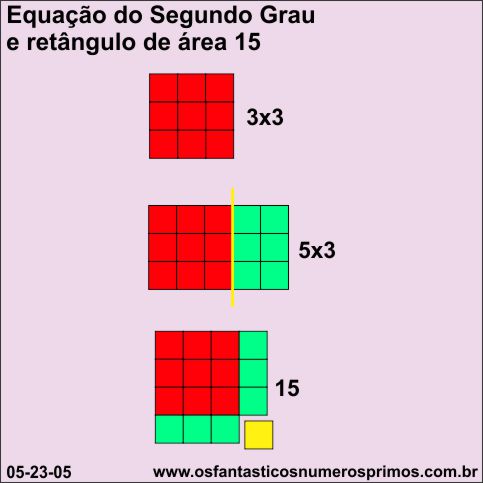
A Equação do Segundo Grau não é um trinômio quadrado perfeito.
x (x+2) = 15
x2 + 2x = 15
dividi-se o coeficiente 2 do termo "bx" por 2 e eleve ao quadrado e some-o ao segundo membro para equilibrar a equação.
x2 + 2x + 12 = 15 + 12
x2 + 2x + 1 = 15 + 1
o primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 2x + 1 = 16
fatora-se o primeiro membro - quadrado da soma (produto notável).
(x + 1)2 = 16
extrai-se a raiz quadrada dos dois membros.
x + 1 = ± √16
x + 1 = ± 4
Solução positiva
x' = + 4 - 1 = 3
Solução negativa
x" = - 4 - 1 = - 5
A soma é 10 e o produto é 24.
Através da adição, o número 10 pode ser obtido:
1 + 9 = 10
2 + 8 = 10
3 + 7 = 10
4 + 6 = 10
5 + 5 = 10
Através da multiplicação o número 24 pode ser obtido:
1 x 24 = 24
2 x 12 = 24
3 x 8 = 24
4 x 6 = 24
O semiperímetro do retângulo é 10 (largura 6 + altura 4).
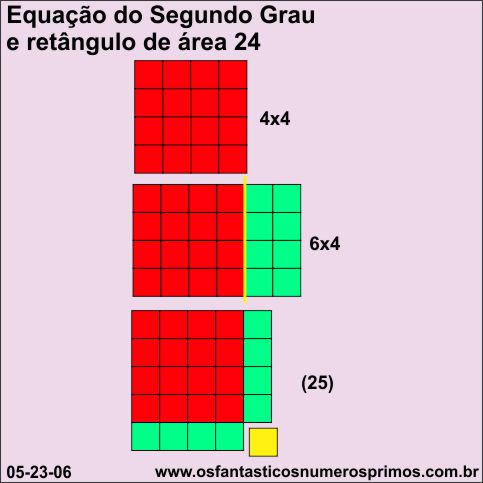
A Equação do Segundo Grau não é um trinômio quadrado perfeito.
x (x+2) = 24
x2 + 2x = 24
dividi-se o coeficiente 2 do termo "bx" por 2 e eleve ao quadrado e some-o ao segundo membro para equilibrar a equação.
x2 + 2x + 12 = 24 + 12
x2 + 2x + 1 = 24 + 1
o primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 2x + 1 = 25
fatora-se o primeiro membro - quadrado da soma (produto notável).
(x + 1)2 = 25
extrai-se a raiz quadrada dos dois membros.
x + 1 = ± √25
x + 1 = ± 5
Solução positiva
x' = + 5 - 1 = 4
Solução negativa
x" = - 5 - 1 = - 6
Através de modelos matemáticos bastantes simples a Equação do Segundo Grau pode ser aprendida de forma lúdica e prazerosa.
Podemos observar pelos exemplos apresentados que vários conceitos matemáticos vão surgindo e sendo aplicados a medida que a equação vai sendo desenvolvida até a sua solução final, como progressões aritméticas e geométricas, produtos notáveis, cálculo de raiz quadrada, números figurados, números inteiros, exponenciação, etc.
Autor: Ricardo Silva - maio/2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
SAUTOY, Marcus Du. Filme The Story of Maths - The Language of The Universe. The Open University - BBC - XXVIII.
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato