capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Divisores de 36 - 259

O número 36 é um número quadrado perfeito e a sua raiz quadrada é o número perfeito 6.

Observação: O número 6 é o primeiro número composto par que não é potência de um número primo ou de outro número composto.

Para se saber quais são os divisores e quantidades de divisores de um número natural utilizamos o algorítmo Decomposição em Fatores Primos.

Decomposição em Fatores Primos
do número 36

	Fatores Primos	Divisores
		1
36	2	2
18	2	4
9	3	3	6	12
3	3	9	18	36
1

Divisores de 36

D(36): 1, 2, 3, 4, 6, 9, 12, 18, 36

Quantidade de divisores de 36

9 divisores

Processo prático para se saber a quantidade de divisores.

36 = 2 x 2 x 3 x 3

36 = 2² x 3²

Soma-se 1 (uma unidade) à cada expoente.

36 = 2^{2 + 1} x 3^{2 + 1}

Multiplica-se as adições nos expoentes.

(2 + 1) x (2 + 1)

3 x 3 = 9

Número 36 e propriedades numéricas

Assim como o número 36, os números 100, 196, 224, ... da tabela abaixo e outros da sequência dos números naturais possuem propriedades numéricas que os diferem de outros números naturais:

Tabelas de Divisores
de Números Quadrados Perfeitos

Raiz	Número	Divisores	Quantidade

6	36	1, 2, 3, 4, 6, 9, 12, 18, 36	9

10	100	1, 2, 4, 5, 10, 20, 25, 50, 100	9

14	196	1, 2, 4, 7, 14, 28, 49, 98, 196	9

15	225	1, 3, 5, 9, 15, 25, 45, 75, 225	9

16	256	1, 2, 4, 8, 16, 32, 64, 128, 256	9

21	441	1, 3, 7, 9, 21, 49, 63, 147, 441	9

22	484	1, 2, 4, 11, 22, 44, 121, 242, 484	9

26	676	1, 2, 4, 13, 26, 52, 169, 338, 676	9

Fonte: Tabela adaptada de

https://pt.wikipedia.org/wiki/Tabela_de_divisores

a) são números quadrados perfeitos;

b) possuem 9 divisores;

b) o termo médio (6, 10, 14,...) é uma raízes quadrada;

f) o termo médio ao quadrado é igual ao último termo de cada sequência;

E outra propriedade numérica muito especial que é a base dos estudos publicado no livro digital Descobrindo Números Primos a partir de Números Compostos é de que potências de números compostos que não potências de números primos, possuem divisores em quantidades de números quadrados perfeitos.

Veja matérias relacionadas.

Número 36 e Quadrados Mágicos Multiplicativos

Elevando-se os divisores de 36 ao quadrado, ao cubo, a quarta potência, a quinta potência e assim sucessivamente são possíveis de construirem Quadrados Mágicos Multiplicativos Sequênciais.

Quadrado Mágico Multiplicativo com divisores de 36 ao quadrado

Constante Mágica 46.656

Soma dos termos 1.911

Quadrado Mágico Multiplicativo 3x3
Divisores de 36
ao quadrado
				46.656
9	1296	4	=	46.656
16	36	81	=	46.656
324	1	144	=	46.656
=	=	=
46.656	46.656	46.656		46.656

Número 36 e Geometria

360 é a quantidade de graus da circunferência.

36 é a décima parte da Circunferência.

36 é um dos ângulos agudos do Triângulo Áureo, também chamado de Triângulo Sublime.

Nas diagonais do pentágono e do dodecágono o número 36 também é um dos ângulos agudos.

Número 36 e os números 3 e 9

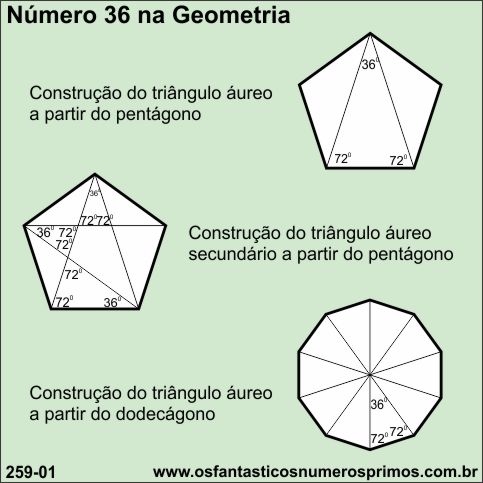
A soma dos algarismos tem como resultado um múltiplo de 3 e 9.

3 + 6 = 9

A produto dos algarismos tem como resultado um múltiplo de 3 e 9

3 x 6 = 18

A diferença entre 36 e a soma dos seus algarimos é múltiplo de 3 e 9

36 - (3 + 6) = 27

A soma de 36 com a soma dos seus alagarismos é um múltiplo de 3 e 9

36 + (3+6) = 45

Autor: Ricardo Silva - maio/2020

Fontes Bibliográficas:

[1] Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

[2] https://pt.www.wikipedia.org/wiki/Tabela_de_divisores