capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Partições de número natural - 260

O algorítmo de Decomposição em Fatores Primos é um método pelo qual podemos saber quais são e as quantidades de divisores de um número natural.

Por meio da decomposição em fatores primos também podemos saber se um número é um número quadrado perfeito, número cúbico perfeito, etc..., bem como, determinar o Mínimo Múltiplo Comum e o Máximo Divisor Comum.

E de quantas maneiras pode-se particionar um número natural, isto é, decompô-lo em somas de números inteiros?

Nos estudos de Srinivasa Ramanujan (1887-1920), em colaboração com Godfrey Hardy (1877–1947) em uma complexa fórmula que envolve raiz quadrada de 2, número pi, números imaginários, funções trigonometricas eles conseguiram por exemplo saber a quantidade aproximada 3.972.999.029.388 de partições do Número 200.

Convenhamos, fazer cálculos em que o arrendamento do resultado é próximo da respota exata de 3.972.999.029.388 são cálculos de Mestres Matemáticos.

Partições e números primos

A seguinte tabela apresenta a quantidade de partições de alguns números naturais.

Número (N)	Partições de N = p(N)
1	1
2	2
3	3
4	5
5	7
6	11
7	15
8	22
9	30
10	42
11	46
12	77
13	101
14	135
15	176
16	231
17	297
18	385
19	490
20	627
21	792
22	1.002
100	190.569.291
1000	24.061.467.864.032.622.473.692.149.727.991

Fonte:

https://cosmovivencias.blogspot.com/2018/12/0155-voltando-particao-dos-numeros.html

Ramanujan em seus estudos com Partições verificou que a quantidade de partições de determinados números são múltiplos de números primos:

a) p(4)=5, p(9)=30, p(14)=135, p(19)=490 são múltiplos de 5;

b) p(5)=7, p(12)=77, p(19)=490 são múltiplo de 7;

c) p(6)=11, p(17)=297 são múltiplo de 11;

Partições e regularidades numéricas

Tabulando informações de alguns números naturais com as suas respectivas partições, pode-se verificar mais padrões e regularidades numéricas.

Partições de Números Naturais

	Quantidade										Quantidade
	números										de
	por										partlçoes
	linha
		Partições
Número 2	1	2
	2	1	1								2
2 x 2 = 4
soma	3	3	1


Número 3	1	3									1
	2	2	1								2
3 x 3 = 9	3	1	1	1							3

soma	9	9	2	1


Número 4	1	4									1
	2	3	1								2
4 x 5 = 20	2	2	2								3
	3	2	1	1							4
	4	1	1	1	1						5

soma	12	12	5	2	1


Número 5	1	5									1
	2	4	1								2
5 x 7 = 35	2	3	2								3
	3	3	1	1							4
	3	2	2	1							5
	4	2	1	1	1						6
	5	1	1	1	1	1					7

soma	20	20	8	4	2	1


Número 6	1	6									1
	2	5	1								2
6 x 11 = 66	2	4	2								3
	3	4	1	1							4
	2	3	3								5
	3	3	2	1							6
	4	3	1	1	1						7
	3	2	2	2							8
	4	2	2	1	1						9
	5	2	1	1	1	1					10
	6	1	1	1	1	1	1				11

soma	35	35	16	8	4	2	1


Número 7	1	7									1
	2	6	1								2
7 x 15 = 105	2	5	2								3
	3	5	1	1							4
	2	4	3								5
	3	4	2	1							6
	4	4	1	1	1						7
	3	3	3	1							8
	3	3	2	2							9
	4	3	2	1	1						10
	5	3	1	1	1	1					11
	4	2	2	2	1						12
	5	2	2	1	1	1					13
	6	2	1	1	1	1	1				14
	7	1	1	1	1	1	1	1			15

soma	54	54	24	13	7	4	2	1


Número 8	1	8									1
	2	7	1								2
8 x 22 = 176	2	6	2								3
	3	6	1	1							4
	2	5	3								5
	3	5	2	1							6
	4	5	1	1	1						7
	2	4	4								8
	3	4	3	1							9
	3	4	2	2							10
	4	4	2	1	1						11
	5	4	1	1	1	1					12
	3	3	3	2							13
	4	3	3	1	1						14
	4	3	2	2	1						15
	5	3	2	1	1	1					16
	6	3	1	1	1	1	1				17
	4	2	2	2	2						18
	5	2	2	2	1	1					19
	6	2	2	1	1	1	1				20
	7	2	1	1	1	1	1	1			21
	8	1	1	1	1	1	1	1	1		22

soma	86	86	41	22	13	7	4	2	1


Número 9	1	9									1
	2	8	1								2
9 x 30 = 270	2	7	2								3
	3	7	1	1							4
	2	6	3								5
	3	6	2	1							6
	4	6	1	1	1						7
	2	5	4								8
	3	5	3	1							9
	3	5	2	2							10
	4	5	2	1	1						11
	5	5	1	1	1	1					12
	3	4	4	1							13
	3	4	3	2							14
	4	4	3	1	1						15
	4	4	2	2	1						16
	5	4	2	1	1	1					17
	6	4	1	1	1	1	1				18
	3	3	3	3							19
	4	3	3	2	1						20
	4	3	2	2	2						21
	5	3	3	1	1	1					22
	5	3	2	2	1	1					23
	6	3	2	1	1	1	1				24
	7	3	1	1	1	1	1	1			25
	5	2	2	2	2	1					26
	6	2	2	2	1	1	1				27
	7	2	2	1	1	1	1	1			28
	8	2	1	1	1	1	1	1	1		29
	9	1	1	1	1	1	1	1	1	1	30

soma	128	128	61	35	20	12	7	4	2	1

www.osfantasticosnumerosprimos.com.br

Partições do número 2

		Partições
Número 2	1	2
2 x 2 = 4	2	1	1	2

soma	3	3	1

O número 2 possui a quantidade de 2 partições.

2 x 2 = 4

4 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 3 é soma da quantidade de números por linha

b) 3 é a soma da primeira coluna das partições

Partições do número 3

Número 3	1	3			1
3 x 3 = 9	2	2	1		2
	3	1	1	1	3

soma	6	6	2	1

O número 3 possui a quantidade de 3 partições.

3 x 3 = 9

9 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 6 é soma da quantidade de números por linha;

b) 6 é a soma da primeira coluna das partições.

Partições do número 4

Número 4	1	4				1
4 x 5 = 20	2	3	1			2
	2	2	2			3
	3	2	1	1		4
	4	1	1	1	1	5

soma	12	12	5	2	1

O número 4 possui a quantidade de 5 partições.

4 x 5 = 20

20 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 12 é soma da quantidade de números por linha;

b) 12 é a soma da primeira coluna das partições.

Partições do número 5

Número 5	1	5					1
5 x 7 = 35	2	4	1				2
	2	3	2				3
	3	3	1	1			4
	3	2	2	1			5
	4	2	1	1	1		6
	5	1	1	1	1	1	7
soma	20	20	8	4	2	1

O número 5 possui a quantidade de 7 partições.

5 x 7 = 35

35 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 20 é soma da quantidade de números por linha;

b) 20 é a soma da primeira coluna das partições.

Partições do número 6

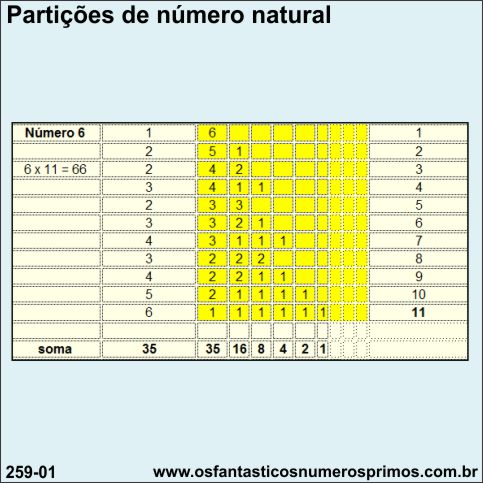
Número 6	1	6						1
6 x 11 = 66	2	5	1					2
	2	4	2					3
	3	4	1	1				4
	2	3	3					5
	3	3	2	1				6
	4	3	1	1	1			7
	3	2	2	2				8
	4	2	2	1	1			9
	5	2	1	1	1	1		10
	6	1	1	1	1	1	1	11

soma	35	35	16	8	4	2	1

O número 6 possui a quantidade de 11 partições.

6 x 11 = 66

66 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 35 é soma da quantidade de números por linha;

b) 35 é a soma da primeira coluna das partições.

Partições do número 7

Número 7	1	7							1
	2	6	1						2
7 x 15 = 105	2	5	2						3
	3	5	1	1					4
	2	4	3						5
	3	4	2	1					6
	4	4	1	1	1				7
	3	3	3	1					8
	3	3	2	2					9
	4	3	2	1	1				10
	5	3	1	1	1	1			11
	4	2	2	2	1				12
	5	2	2	1	1	1			13
	6	2	1	1	1	1	1		14
	7	1	1	1	1	1	1	1	15

soma	54	54	24	13	7	4	2	1

O número 7 possui a quantidade de 15 partições.

7 x 15 = 105

105 é a soma de todos dos números das partições.

A soma da quantidade de números por linha das partições é igual a soma da primeira coluna da partição:

a) 54 é soma da quantidade de números por linha;

b) 54 é a soma da primeira coluna das partições.

Partições e duplas de números distintos

Nas partições de números naturais ocorrem duplas de números distintos os quais podem ser utilizados como raízes de Equações do Segundo Grau.

Número 5	1	5					1
5 x 7 = 35	2	4	1				2
	2	3	2				3
	3	3	1	1			4
	3	2	2	1			5
	4	2	1	1	1		6
	5	1	1	1	1	1	7
soma	20	20	8	4	2	1

Exemplo:

A dupla 3 e 2 pode ser utilizada em uma equação produto para formar um Trinômio do Segundo Grau:

(x-2) . (x-3) = 0

x - 5x + 6 = 0

x - 5x + 6 = (x-2) . (x-3)

Autor: Ricardo Silva - maio/2020

Fontes Bibliográficas:

Du Sautoy, Marcus, 1965. A música dos números primos: uma história de um problema não resolvido na matemática / Marcus du Sautoy, Diego Alfaro. - Rio de Janeiro: Jorge Zahar Ed., 2007

https://cosmovivencias.blogspot.com/2018/12/0155-voltando-particao-dos-numeros.html