capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Demonstração do Teorema de Pitágoras por J. Adams - 300

No livro The Phitagorean Proposition, edição de 1940, página 116, do Professor estadunidense Elisha Escott Loomis se encontra a demonstração de número 27, cuja autoria é de J. Adams a qual foi enviada ao Professor em 1933.

É uma demonstração do Teorema de Pitágoras que apresenta características construtivas bastante interessante, verificando as demais demonstrações geométricas publicadas no referido livro, a do Sr. J. Adams é a única demonstração geométrica em que nos quadrados dos catetos há quadrado inscrito em cada um deles.

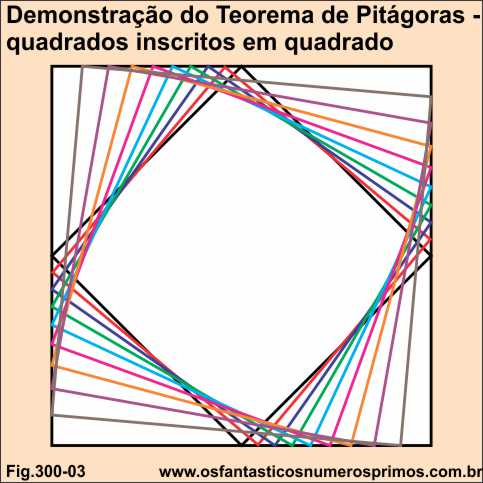
Então me fiz a seguinte pergunta, quantos quadrados podem ser inscritos em um quadrado de forma que os vértices desses quadrados inscritos tangenciem o quadrado principal?

Demonstração do Teorema de Pitágoras por J. Adams

Demonstração do Teorema de Pitágoras - quadrados dinâmicos

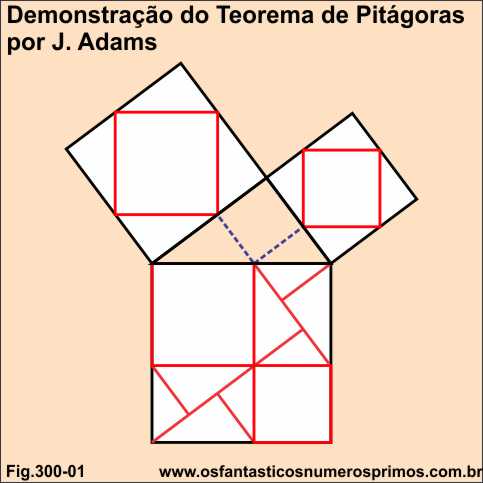
Construindo-se quadrados unidos a partir dos seus pontos médios obtêm-se sequências de quadrados cujos lados são números inteiros e outra cujos lados são números irracionais.

Demonstração do Teorema de Pitágoras - quadrados inscritos em quadrado

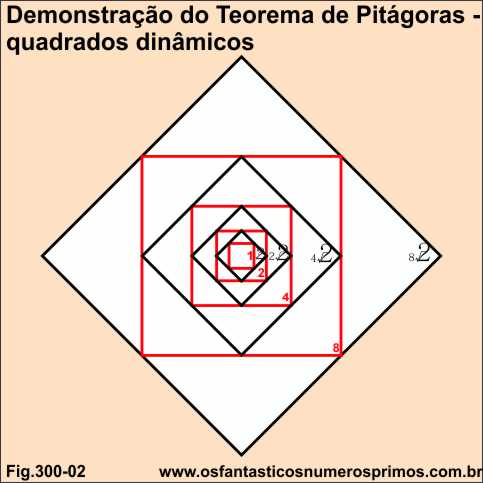
Inscrevendo-se quadrados em um quadrado principal a partir dos seus pontos médios e inclinando-os a cada 5 graus, obtêm-se 9 quadrados de lados variáveis cujos vértices interceptam o quadrado principal.

demonstração teorema de pitágoras - quadrados inscritos em quadrado

Demonstração do Teorema de Pitágoras por J. Adams - construção geométrica 1

A partir de um triângulo retângulo escaleno ABC e quadrados construídos sobre seus lados procedemos com as seguintes etapas:

a) transporta-se a medida AB para a hipotenusa, obtendo-se CD;

b) traça-se DE paralela a AB;

c) traça-se DF paralela a AC;

d) a partir de E, traça-se seguimentos formando-se o QUADRADO INSCRITO - 1 no quadrado do cateto maior;

e) a partir de F, traça-se seguimentos formando-se o QUADRADO INSCRITO - 2 no quadrado do cateto menor;

f) traça-se a diagonal DG;

g) traça-se o seguimento GH;

i) traça-se a diagonal IJ, prolongando-a até DG;

j) prolonga-se DJ, obtendo-se JK;

k) a partir de H e K traçe paralelas a AB, obtendo-se os triângulos T-2, T-4, T-5 e T-7;

k) a partir de B traçe paralela a AC, obtendo-se os triângulos T-1, T-3, T-6 e T-8;

Nesta belíssima construção originou-se simultaneamente dois conjuntos de 4 triângulos congruentes e dois quadrados que se encaixam perfeitamente nos quadrados dos catetos bem como no quadrado da hipotenusa.

Interessante observar que no quadrado do cateto maior se encontram o quadrado e os triângulos maiores e no quadrado do cateto menor, o quadrado e os triângulos menores.

No quadrado da hipotenusa, os triângulos maiores e menores e em duplas formam dois retângulos congruentes cujos lados maiores são as hipotenusas dos triângulos maiores e os lados menores as hipotenusas de triângulos menores.

Na demonstração de J. Adams, como se observa, está incorporada em sua construção a Demonstração do Teorema de Pitágoras por comparação de áreas, pois cada quadrado sobre cada cateto é formado por um quadrado inscrito cujos lados são triângulos retângulos congruentes, demonstração esta que pode ter sido feita pelo próprio Pitágoras, como acreditam certos estudiosos.

demostração teorema de pitágoras por J. Adams - construção

Demonstração do Teorema de Pitágoras por J. Adams - construção geométrica 2

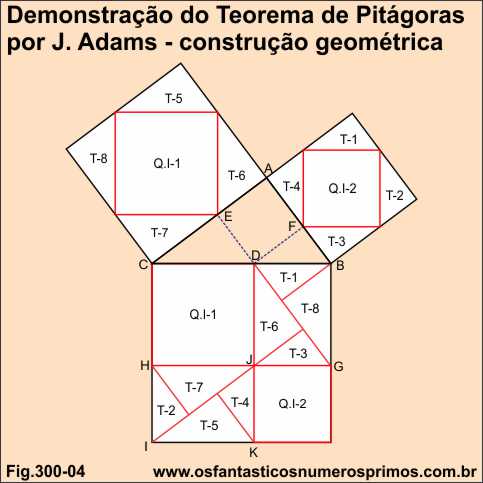
A Demostração de J. Adams também pode ser construída de uma outra forma obtendo-se o mesmo resultado, vejamos:

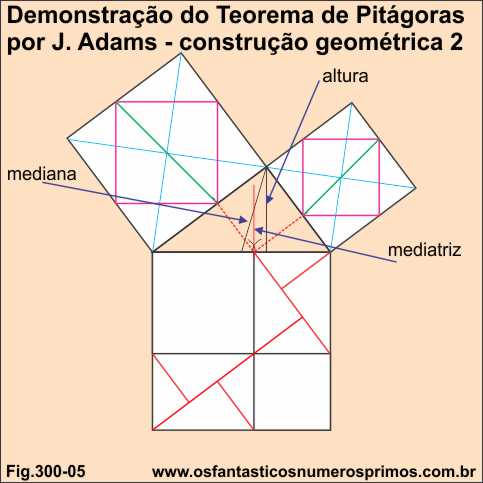
a) traça-se o seguimento relativo à altura da hipotenusa no triângulo retângulo;

b) traça-se a mediana;

c) traça uma mediatriz entre a intersecções da altura relativa à hipotenusa e a mediana obtendo-se o ponto médio;

d) a partir do ponto médio traça-se duas paralelas (linhas pontilhadas vermelhas); uma paralela ao cateto maior intesectando o cateto menor, outra paralela ao cateto menor intersectando o cateto maior

e) a partir de cada intersecção traça-se seguimentos (linhas verdes) de 45 graus tendo como base a hipotenusa; do cateto maior até o lado oposto do quadrado; do cateto menor até o lado oposto do quadrado;

f) das intersecções dos seguimentos (linhas verdes) constrõem-se quadrados inscritos (quadrados lilázes);

g) para finalizar, traçar seguimentos paralelos (linhas vermelhas) para se obterem os triângulos sobre os retângulos no quadrado da hipotenusa.

Interessante observar que os seguimentos (linhas azuis) são as diagonais dos quadrados dos catetos e que umas das diagonais intersectam simultaneamente os dois quadrados.

demostração teorema de pitágoras por J. Adams - construção 2

Autor: Ricardo Silva - novembro/2020

Fontes Bibliográficas:

LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014