


No Canal do YouTube: Equaciona Com Paulo Pereira - vídeo: A matemática é linda - Teorema de Pitágoras Aplicação #5, o Professor Paulo Pereira demonstra duas resoluções de um problema matemático que envolve Teorema de Pitágoras, enviado por um de seus Admiradores, o Jean.
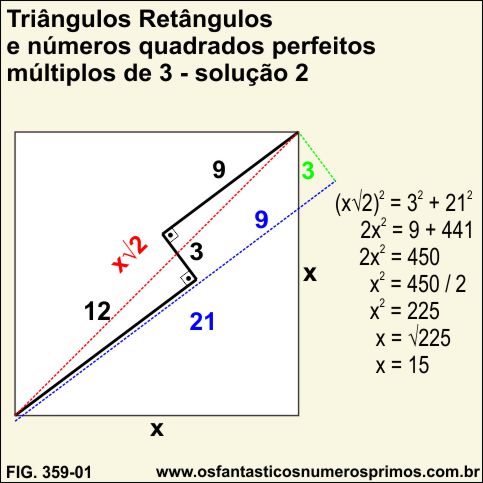
Fonte: Equaciona Com Paulo Pereira - A matemática é linda - Teorena de Pitágoras Aplicação #5 - YouTube
O problema consiste em determinar a medida do lado de um quadrado cujo interior apresenta seguimentos de retas que partem de um dos vértices e terminam em outro com as seguintes medidas: 12, 3 e 9 formando um "degrau de uma escada"
Brilhantemente, o Professor Paulo Pereira demonstra duas soluções, determinando a medida do lado do quadrado cuja a medida é 15, um número inteiro.
Na segunda solução do problema e de uma forma não trivial conforme a figura 359-01, o Professor Paulo Pereira determina a medida do lado do quadrado utilizando-se a expressão x√2 que representa a medida da diagonal de um quadrado utilizando a projeção de um triângulo retângulo escaleno cuja hipotenusa é a diagonal do quadrado.
O Professor prolonga o segmento de medida 12 e projetando o segmento de medida 9 sobre este prolongamento, obtem o cateto maior de medida 21. Desloca o segmento de medida 3, fazendo-o tocar no vértice direito superior do quadrado e do prolongamento anterior, obtendo-se assim, o cateto de medida 3 projetando um triângulo retângulo escaleno.
O que chamou a minha atenção é que a estratégia de se utilizar a expressão x√2 da diagonal do quadrado, resultou em encontrar a medida do lado do quadrado cujo resultado é um número inteiro e as medidas dos seguimentos que formam o "degrau de uma escada'' são todos números múltiplos de 3: 3, 9 e 12.
Na figura 359-02, tem-se outra resolução do problema cujos resultados são todos números irracionais e o interessante é que a soma das hipotenusas dos triângulos retângulos escalenos: (3, 9, x=9,486) e (3, 12, x=12,369) é 21,855..., um número próximo a medida da diagonal de um quadrado cuja a medida do lado é 15, pois 15 √2 = 21,213...

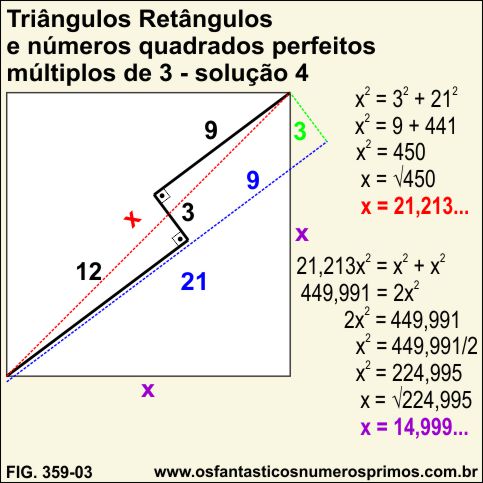
Na figura 359-03, tem-se outra resolução do problema cujos resultados são todos números irracionais.
A diagonal do quadrado e consequentemente a hipotenusa do triângulo retângulo de catetos 3 e 21 está com a incógnita x (xis) e não x √2.
A medida da hipotenusa é 21,213... e a medida do lado do quadrado é 14,999... que são números irracionais.
O triângulo retângulo de catetos 3 e 21 formado a partir de seguimentos que aparentam um "degrau de uma escada" e cujas medidas são números múltiplos de 3 possui características especias como triângulos retângulos pitagóricos, pois substituindo-se a incógnita x (xis) da hipotenusa por x√2 obtêm um número inteiro que corresponde a medida do lado do quadrado no qual o triângulo retângulo é construído.
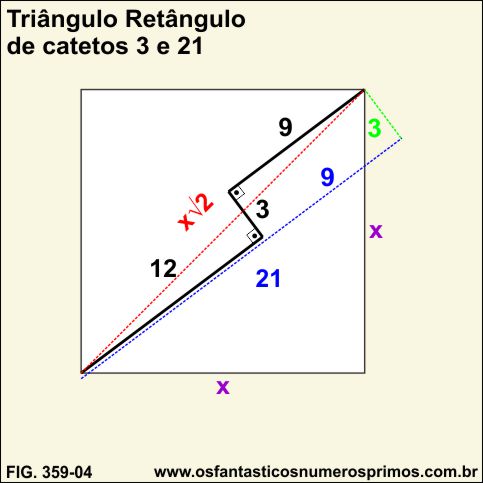
Fazendo análises dos termos no Teorema de Pitágoras, a soma dos quadrados dos catetos tem como resultado 450 e dividindo-o por 2, obtem-se o quadrado 225 cuja raiz quadrada é 15, um número inteiro.
| (x√2)2 | = | 32 + 212 |
| 2x2 | = | 9 + 441 |
| 2x2 | = | 450 |
| x2 | = | 450 / 2 |
| x2 | = | 225 |
| x | = | √225 |
| x | = | 15 |
Partindo-se dessas análises, encontrou-se outras raras sequências de números com características numéricas semelhantes a 12, 3 e 9 bem como 3 e 21.
Fixando-se os números 3 e 9 e variando-se múltiplos de 3 de 3 a 3000, foram encontradas as seguintes sequências:
Somando-se 9 + 114 = 123 e substituindo na equação.
| (x√2)2 | = | 32 + 1232 |
| 2x2 | = | 9 + 15.129 |
| 2x2 | = | 15.138 |
| x2 | = | 15.138 / 2 |
| x2 | = | 7.569 |
| x | = | √7.569 |
| x | = | 87 |
Somando-se 9 + 708 = 717 e substituindo na equação.
| (x√2)2 | = | 32 + 7172 |
| 2x2 | = | 9 + 514.089 |
| 2x2 | = | 514.098 |
| x2 | = | 514.098 / 2 |
| x2 | = | 257.049 |
| x | = | √257.049 |
| x | = | 507 |
Fixando-se os números 6 e 36 e variando-se múltiplos de 6 de 6 a 6060, foram encontradas as seguintes sequências:
Somando-se 6 + 36 = 42 e substituindo na equação.
| (x√2)2 | = | 62 + 422 |
| 2x2 | = | 36 + 1.764 |
| 2x2 | = | 1.800 |
| x2 | = | 1.800 / 2 |
| x2 | = | 900 |
| x | = | √900 |
| x | = | 30 |
Somando-se 36 + 210 = 246 e substituindo na equação.
| (x√2)2 | = | 62 + 2462 |
| 2x2 | = | 36 + 60.516 |
| 2x2 | = | 60.552 |
| x2 | = | 60.552 / 2 |
| x2 | = | 30.276 |
| x | = | √30.276 |
| x | = | 174 |
Somando-se 36 + 1398 = 1434 e substituindo na equação.
| (x√2)2 | = | 62 + 14342 |
| 2x2 | = | 36 + 2.056.356 |
| 2x2 | = | 2.056.392 |
| x2 | = | 2.056.392 / 2 |
| x2 | = | 1.028.196 |
| x | = | √1.028.196 |
| x | = | 1014 |
Autor: Ricardo Silva - fevereiro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Equaciona Com Paulo Pereira - A matemática é linda - Teorena de Pitágoras Aplicação #5 - YouTube

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato