capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

O quadrado e os triângulos pitagórico e de 30, 60 e 90 graus - 370

Entre as várias demonstrações do Teorema de Pitágoras, há uma que segundo historiadores seria a demonstração utilizada pela Escola Pitagórica que é a demonstração do tipo "geométrico", isto é, por comparação de áreas.

teorema de pitágoras por comparação de áreas

Vejamos:

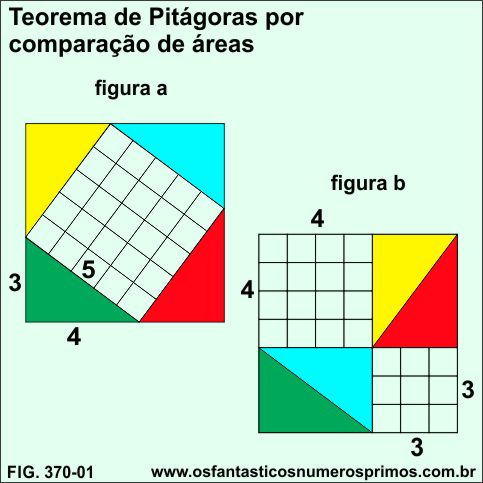
Constroi-se um quadrado com 4 triângulos retângulos conforme disposição geométrica da figura a.

No exemplo, tem-se 4 triângulos retângulos de lados 3, 4 e 5 unidades.

No interior do quadrado da figura a, as hipotenusas formam um quadrado quadriculado de lado 5, perfazendo uma área de 25 unidades quadradas.

Posteriormente, constroi-se outro quadrado conforme disposição geométrica da figura b.

As duas áreas quadriculadas que se formam são às áreas dos catetos maior e menor e que somadas equivalem á area da hipotenusa:

4 x 4 = 16

3 x 3 = 9

16 + 9 = 25

Comprovando o que diz o Teorema de Pitágoras: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.

Nas demonstrações que se seguiram, fez-se o uso do Triângulo Pitagórico 3-4-5, na verdade, pode-se utilizar triângulos retângulos de quaisquer medidas e ângulos.

Triângulo equilátero a partir da Vesica Piscis

Triângulo equilátero é um triângulo cujos lados têm medidas iguais e ângulos internos de 60 graus.

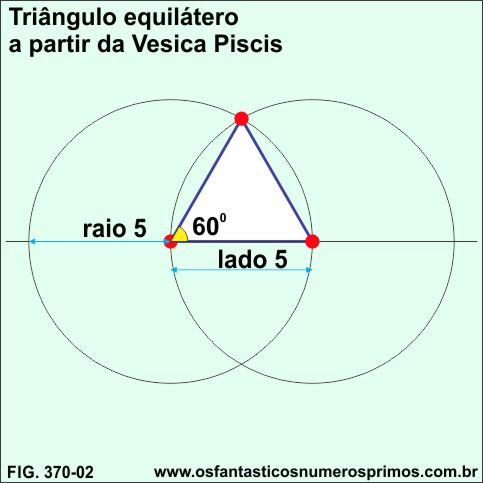
Um dos métodos para se construir triângulo equilátero é por meio da Vesica Piscis que é uma construção geométrica com duas circunferências de mesmo raio na qual o centro de uma está sobre a circunferência da outra.

No exemplo, cada circunferência tem raio de 5 unidades e diâmetro de 10 unidades.

Unindo com seguimento o centro das circunferências e posteriormente de cada centro até a intersecção destas, forma-se um triângulo equilátero cujos lados são de 5 unidades.

Triângulo retângulo de 30, 60 e 90 graus

Traçando um segmento perpendicular a partir do ponto médio de um dos lados do triângulo equilátero até um de seus vértices, obtem-se uma de suas alturas e consequentemente a divisão em dois triângulos retângulos de 30, 60 e 90 graus.

Vale observar que o triângulo equilátero de lados de 5 unidades foi gerado a partir da Vesica Piscis e que ao ser dividido, obteve-se dois triângulos retângulos de catetos medindo 2,5 e 4,33 e hipotenusa de 5 unidades.

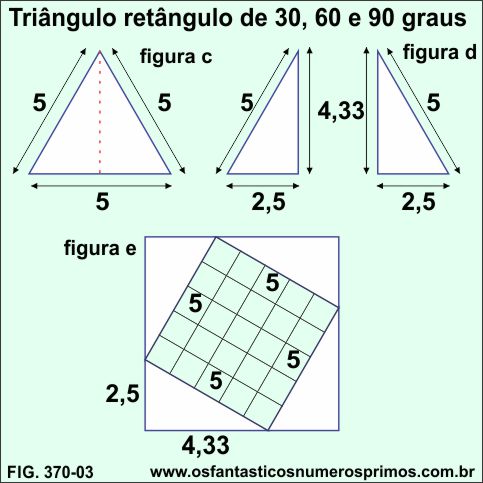
Como dito acima, a demonstração do Teorema de Pitágoras por comparação de área, pode ser feita com triângulos retângulos de quaisquer medidas e ângulos.

Dispondo 4 triângulos retângulos de ângulos de 30, 60 e 90 graus, de catetos 2,5 e 4,33 e hipotenusa 5 unidades, obtem-se demonstração semelhante acima e com um quadrado quadriculado de área de 25 unidades mesmo tendo um dos catetos medida de um número irracional.

A metade do lado do triângulo equilátero 2,5 multiplicado por √3 = 4,3301... é a medida de sua altura e consequentemente a medida dos catetos maior nos dois triângulos retângulos gerados em sua divisão.