


Números figurados, também denominados de geométricos, são números que por meio de arranjos de pontos podemos formar figuras geométricas de triângulos, retângulos, quadrados, pentágonos, etc...
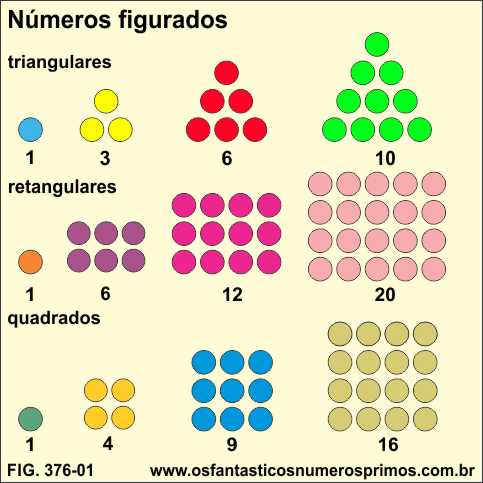
Números triangulares também podem ser obtidos por meio:
1) da soma de números consecutivos;
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
2) do produto de dois números consecutivos e posteriormente dividindo por 2.
Observação: o produto de dois números consecutivos têm como resultado número retangular (número oblongo).
a)
1 x 2 = 2
2 : 2 = 1
b)
2 x 3 = 6
6 : 2 = 3
c)
3 x 4 = 12
12 : 2 = 6
Com 153 pontos pode-se representar tanto triângulo retângulo quanto triângulo equilátero.
A soma consecutiva dos 17 primeiros números naturais tem como resultado o número triangular 153.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 = 153.
O último número das parcelas determina a ordem / posição do triangular 153, a posição de número 17.
Na construção de triângulo retângulo de 153 pontos, pode-se inscrever dois outros triângulos retângulos de 36 e 45 pontos formando um quadrado de 81 pontos.
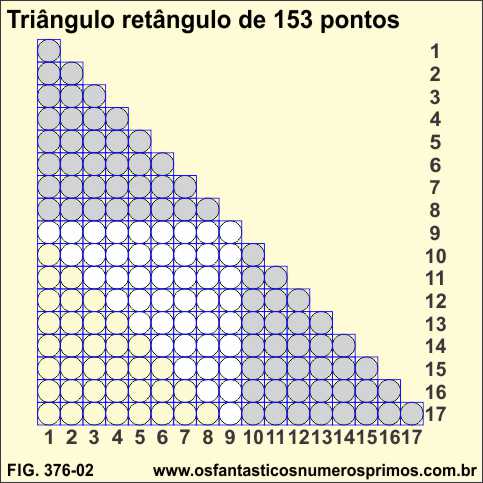
Somando-se os dois triângulos retângulos: (36 + 45 = 81), que são dois números triangulares consecutivos, o resultado é o quadrado inscrito de 81 pontos.
O número 9 é a raiz quadrada de 81, que é o quadrado inscrito no triângulo retângulo de 153 pontos.
No triângulo equilátero, pode-se inscrever em seu centro, um outro triângulo equilátero de 45 pontos.
O triangular 153 por estar em uma ordem / posição ímpar (170 lugar) é o que determina ter um outro triângulo equilátero inscrito.

Além de suas propriedades geométricas, o número triangular 153 possui diversas outras propriedades numéricas interessantes relacionadas à outras sequências numéricas como: números poligonais, números perfeitos, números quadrados perfeitos, números cúbicos, ternos pitagóricos, bem como, com as suas próprias ordens / posições, etc..., cujos estudos incluem: Teólogos, Numerólogos, Esotéricos, Cabalistas, Matemáticos, Entusiastas Matemáticos, etc...
| Fatores | Divisores | |||
| primos | ||||
| 1 | ||||
| 153 | 3 | 3 | ||
| 51 | 3 | 9 | ||
| 17 | 17 | 17 | 51 | 153 |
| 1 | ||||
D(153): {1, 3, 9, 17, 51, 153}
Quantidade de divisores: 6.
6 é número perfeito e triangular.
3 x 3 x 17 =
= 9 x 17 = 153
153 é produto do quadrado 9 (par de primos) por 17 (outro primo).
1530 = 1 ( 1 divisor ).
1531 = 153 ( 6 divisores ) número perfeito.
1532 = 23.409 ( 15 divisores ).
1533 = 3.581.577 ( 28 divisores ) número perfeito.
1534 = 547.981.281 ( 45 divisores ).
1535 = 83.841.135.993 ( 66 divisores).
As potências de base 153, assim como os produtos de um par de primos por outro primo distinto, não são potências de números primos ou de outros números compostos.
Os produtos de um par de primos por outro primo distinto geram números que são bases de potências cujas quantidades de divisores são em números triangulares não consecutivos.
Observação importante: os textos acima fazem parte de estudos publicados na coleção de livros digitais sobre sequências numéricas e também aqui no WebSite Os Fantásticos Números Primos.
Assim como o número 153, os números: 0, 1, 370, 371 e 407 podem ser expressos com a soma dos cubos de seus algarismos.
13 53 33 = 1 + 125 + 27 = 153
03 = 0
13 = 1
33 73 03 = 27 + 343 + 0 = 370
33 73 13 = 27 + 343 + 1 = 371
O número 153 é igual a soma dos fatorias de 1 a 5.
1! + 2! + 3! + 4! + 5! =
= 1 + 2 + 6 + 24 + 120 = 153
A soma dos algarimos do número 153 é um quadrado perfeito.
1 + 3 + 5 = 9 = 32
A soma dos divisores do número 153 é um quadrado perfeito.
1 + 3 + 9 + 17 + 51 = 81 = 92
O reverso do número 153 é também um número triangular.
531 é 260 número triangular.
O número 153 é divisível pela soma de seus algarismos.
1 + 5 + 3 = 9
153 : 9 = 17
A soma do divisores do número 153 é 234.
1 + 3 + 9 + 17 + 51 + 153 = 234
A soma dos algarismos do número 234 é um quadrado perfeito
2 + 3 + 4 = 9 = 32
O produto dos divisores próprios de 153 por 234 é 23.409
1 x 3 x 9 x 17 x 51 = 23.409
No número 23.409 aparece a soma dos divisores de 153 (234) e a raiz quadrada (09) da soma dos divisores próprios que é 81.
Escolha aleatoriamente um número múltiplo de 3 e prosseguindo com as etapas abaixo, o resultado final é sempre o número 153:
Exemplo 1)
a) separe os algarismos em classes, eleve ao cubo e some-os;
63 = 216
b) repete-se o processo com o número 216;
23 + 13 + 63 = 8 + 1 + 216 = 225
c) repete-se o processo com o número 225;
23 + 23 + 53 = 8 + 8 + 125 = 141
d) repete-se o processo com o número 141;
13 + 43 + 13 = 1 + 64 + 1 = 66
e) repete-se o processo com o número 66;
63 + 63 = 216 + 216 = 432
f) repete-se o processo com o número 432;
43 + 33 + 23 = 64 + 27 + 8 = 99
g) repete-se o processo com o número 99;
93 + 93 = 729 + 729 = 1458
h) repete-se o processo com o número 1458;
13 + 43 + 53 + 83 = 1 + 64 + 125 + 512 = 702
i) repete-se o processo com o número 702;
73 + 03 + 23 = 343 + 0 + 8 = 351
j) repete-se o processo com o número 351;
33 + 53 + 13 = 27 + 125 + 1 = 153
k) o resultado é o número 153.
Exemplo 2)
a) separe os algarismos em classes, eleve ao cubo e some-os;
13 + 23 = 1 + 8 = 9
b) repete-se o processo com o número 9;
93 = 729
c) repete-se o processo com o número 729;
73 + 23 + 93 = 343 + 8 + 729 = 1080
d) repete-se o processo com o número 1080;
13 + 03 + 83 + 03 = 1 + 0 + 512 + 0 = 513
e) repete-se o processo com o número 513;
53 + 13 + 33 = 125 + 1 + 27 = 153
f) o resultado é o número 153.
Autor: Ricardo Silva - abril / 2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org
www.shyamsundergupta.com/
www.mathpages.com

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato