


O número 12 é o primeiro número composto que é produto de um par de números primos por um outro primo ( 2 x 2 x 3 = 12 ou um quadrado por um primo 4 x 3 = 12) e apresenta diversas outras propriedades matemáticas publicadas aqui no WebSite Os Fantásticos Números Primos, bem como, no livro digital Números Perfeitos e Sequências Numéricas (veja matérias relacionadas abaixo).
Os novos estudos que se seguem demostram outras propriedades numéricas relacionadas entre múltiplos de 12 e números primos com números triangulares, potências de números primos e também com números compostos que não são múltiplos de 3.
Determinados múltiplos de 12 subtraídos 1 unidade e extraídas as raízes quadradas têm como resultados números primos.
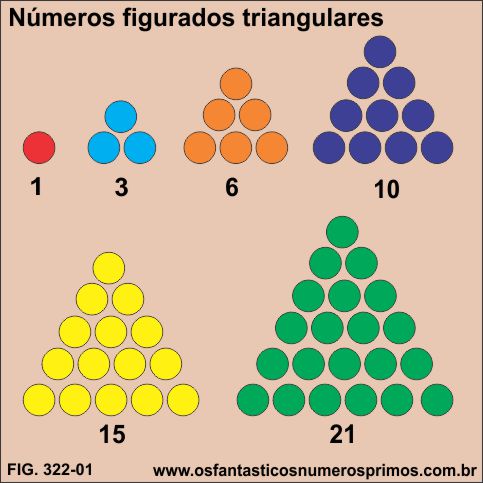
Números triangulares também denominados de números figurados, números geométricos, números poligonais são números formados por meio de arranjos de pontos formando figuras geométricas de triângulos.
1, 3, 6, 10 , 15, 21, 28, 36,... são números triagulares.
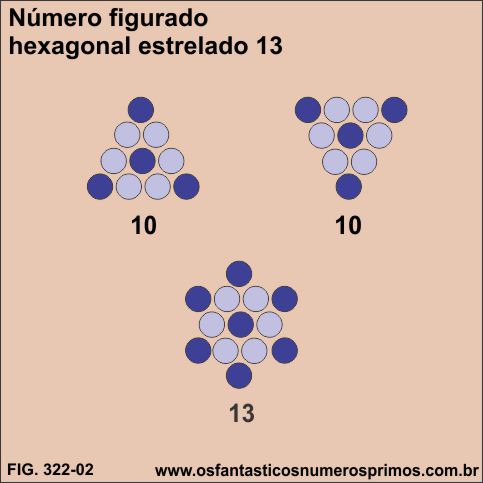
Sobrepondo-se 2 triângulos formados por determinados números figurados triangulares obtêm-se hexágonos estrelados que por sua vez formam a sequência de números figurados hexagonais estrelados.
Sobrepondo-se 2 triângulos de 10 pontos, forma-se o primeiro hexágono estrelado com 13 pontos.
No centro de cada triângulo há um hexágono de 7 pontos.
No número figurado hexágonal estrelado há um hexágono de 7 pontos mais 6 pontos formando as pontas da estrela - total de pontos 13.
13, 37, 73, 121, 181, 253, 337, 433, 541, 661, ... são números figurados hexagonais estrelados.
Entre os números figurados hexagonais estrelados há ocorrências de números primos: 13, 37, 73, 181, 337, 433, 541, 661,...
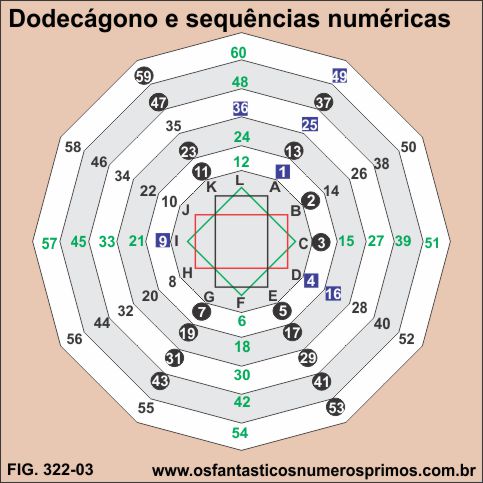
Construindo-se vários dodecágonos equidistantes, figura geométrica composto por 12 lados e 12 vértices, e os numerando sequencialmente seus vértices em espiral do centro para as extremidades, os números primos tendem a se alinharem nos vértices A, E, G e K.
No vértice A, tendem a se alinharem números quadrados perfeitos ímpares cujas raízes quadradas são números primos, bem como, números hexagonais estrelados.
O produto do número 12 por um número triangular somado de 1 unidade têm como resultados números figurados hexagonais estrelados.
A seguinte tabela apresenta os 15 primeiros números figurados hexagonais estrelados.
| número | número | |||||
|---|---|---|---|---|---|---|
| triangular | hexagonal | |||||
| ordem / | estrelado | |||||
| posição | ||||||
| 1 | 1 | x | 12 | + | 1 | 13 |
| 2 | 3 | x | 12 | + | 1 | 37 |
| 3 | 6 | x | 12 | + | 1 | 73 |
| 4 | 10 | x | 12 | + | 1 | 121 |
| 5 | 15 | x | 12 | + | 1 | 181 |
| 6 | 21 | x | 12 | + | 1 | 253 |
| 7 | 28 | x | 12 | + | 1 | 337 |
| 8 | 36 | x | 12 | + | 1 | 433 |
| 9 | 45 | x | 12 | + | 1 | 541 |
| 10 | 55 | x | 12 | + | 1 | 661 |
| 11 | 66 | x | 12 | + | 1 | 793 |
| 12 | 78 | x | 12 | + | 1 | 937 |
| 13 | 91 | x | 12 | + | 1 | 1093 |
| 14 | 105 | x | 12 | + | 1 | 1261 |
| 15 | 120 | x | 12 | + | 1 | 1441 |
| www.osfantasticosnúmerosprimos.com.br | ||||||
Múltiplos de 12 somados com 1 unidade têm como resultados números ímpares e entre eles ocorrências de números quadrados perfeitos cujas raízes quadradas são números primos.
Na sequência de múltiplos de 12 somados com 1 unidade, não há ocorrências de números múltiplos de 3, pois, não há números que somando os seus algarismos sejam múltiplos de 3.
| múltiplos | ||||
|---|---|---|---|---|
| posição / | de | 1 | raiz | |
| ordem | 12 | unidade | soma | quadrada |
| 1 | 12 | 1 | 13 | 3,605551275 |
| 2 | 24 | 1 | 25 | 5 |
| 3 | 36 | 1 | 37 | 6,08276253 |
| 4 | 48 | 1 | 49 | 7 |
| 5 | 60 | 1 | 61 | 7,810249676 |
| 6 | 72 | 1 | 73 | 8,544003745 |
| 7 | 84 | 1 | 85 | 9,219544457 |
| 8 | 96 | 1 | 97 | 9,848857802 |
| 9 | 108 | 1 | 109 | 10,44030651 |
| 10 | 120 | 1 | 121 | 11 |
| 11 | 132 | 1 | 133 | 11,53256259 |
| 12 | 144 | 1 | 145 | 12,04159458 |
| 13 | 156 | 1 | 157 | 12,52996409 |
| 14 | 168 | 1 | 169 | 13 |
| 15 | 180 | 1 | 181 | 13,45362405 |
| 16 | 192 | 1 | 193 | 13,89244399 |
| 17 | 204 | 1 | 205 | 14,31782106 |
| 18 | 216 | 1 | 217 | 14,73091986 |
| 19 | 228 | 1 | 229 | 15,13274595 |
| 20 | 240 | 1 | 241 | 15,5241747 |
| 21 | 252 | 1 | 253 | 15,90597372 |
| 22 | 264 | 1 | 265 | 16,2788206 |
| 23 | 276 | 1 | 277 | 16,64331698 |
| 24 | 288 | 1 | 289 | 17 |
| 25 | 300 | 1 | 301 | 17,34935157 |
| 26 | 312 | 1 | 313 | 17,69180601 |
| 27 | 324 | 1 | 325 | 18,02775638 |
| 28 | 336 | 1 | 337 | 18,35755975 |
| 29 | 348 | 1 | 349 | 18,68154169 |
| 30 | 360 | 1 | 361 | 19 |
| 31 | 372 | 1 | 373 | 19,31320792 |
| 32 | 384 | 1 | 385 | 19,62141687 |
| 33 | 396 | 1 | 397 | 19,92485885 |
| 34 | 408 | 1 | 409 | 20,22374842 |
| 35 | 420 | 1 | 421 | 20,51828453 |
| 36 | 432 | 1 | 433 | 20,80865205 |
| 37 | 444 | 1 | 445 | 21,09502311 |
| 38 | 456 | 1 | 457 | 21,37755833 |
| 39 | 468 | 1 | 469 | 21,65640783 |
| 40 | 480 | 1 | 481 | 21,9317122 |
| 41 | 492 | 1 | 493 | 22,20360331 |
| 42 | 504 | 1 | 505 | 22,47220505 |
| 43 | 516 | 1 | 517 | 22,737634 |
| 44 | 528 | 1 | 529 | 23 |
| 45 | 540 | 1 | 541 | 23,2594067 |
| 46 | 552 | 1 | 553 | 23,51595203 |
| 47 | 564 | 1 | 565 | 23,76972865 |
| 48 | 576 | 1 | 577 | 24,0208243 |
| 49 | 588 | 1 | 589 | 24,2693222 |
| 50 | 600 | 1 | 601 | 24,51530134 |
| www.osfantasticosnúmerosprimos.com.br | ||||
As diferenças entre as raízes quadradas apresentam o seguinte padrão
| raízes | diferenças |
|---|---|
| 5 | 2 |
| 7 | 4 |
| 11 | 2 |
| 13 | 4 |
| 17 | 2 |
| 19 | 4 |
| 23 | 2 |
| 25 | 4 |
| 29 | 2 |
| 31 | 4 |
| 35 | 2 |
| 37 | 4 |
| 41 | 2 |
| 43 | 4 |
| 47 | 2 |
| 49 | 4 |
| 53 | 2 |
| 55 | 4 |
| 59 | 2 |
| 61 | 4 |
| 65 | 2 |
| 67 | 4 |
| 71 | 2 |
| 73 | 4 |
| 77 | 2 |
| 79 | 4 |
| 83 | 2 |
| 85 | 4 |
| 89 | 2 |
| 91 | 4 |
| www.osfantasticosnúmerosprimos.com.br | |
Rearrajando os múltiplos de 12 somados com 1 unidade em linhas e colunas observa-se que:
a) os números quadrados perfeitos ímpares tendem a se organizarem nas colunas 2, 4 e 10;
b) na coluna 2, há ocorrências de números quadrados de finais 5;
c) na coluna 4, há ocorrências de números quadrados de finais 9;
d) na coluna 10, há ocorrências de números quadrados de finais 1.
| Múltiplos de 12 | ||||||||||
| somados de 1 unidade | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 13 | 25 | 37 | 49 | 61 | 73 | 85 | 97 | 109 | 121 |
| 1 | 133 | 145 | 157 | 169 | 181 | 193 | 205 | 217 | 229 | 241 |
| 2 | 253 | 265 | 277 | 289 | 301 | 313 | 325 | 337 | 349 | 361 |
| 3 | 373 | 385 | 397 | 409 | 421 | 433 | 445 | 457 | 469 | 481 |
| 4 | 493 | 505 | 517 | 529 | 541 | 553 | 565 | 577 | 589 | 601 |
| 5 | 613 | 625 | 637 | 649 | 661 | 673 | 685 | 697 | 709 | 721 |
| 6 | 733 | 745 | 757 | 769 | 781 | 793 | 805 | 817 | 829 | 841 |
| 7 | 853 | 865 | 877 | 889 | 901 | 913 | 925 | 937 | 949 | 961 |
| 8 | 973 | 985 | 997 | 1009 | 1021 | 1033 | 1045 | 1057 | 1069 | 1081 |
| 9 | 1093 | 1105 | 1117 | 1129 | 1141 | 1153 | 1165 | 1177 | 1189 | 1201 |
| 10 | 1213 | 1225 | 1237 | 1249 | 1261 | 1273 | 1285 | 1297 | 1309 | 1321 |
| www.osfantasticosnúmerosprimos.com.br | ||||||||||
Múltiplos de 12 de finais 4 somados com 1 unidade têm como resultados números de finais 5.
Na coluna raiz quadrada há um único número primo que é o número 5.
| múltiplos | ||||
|---|---|---|---|---|
| posição | de | 1 | raiz | |
| ordem | 12 | unidade | soma | quadrada |
| 2 | 24 | 1 | 25 | 5 |
| 12 | 144 | 1 | 145 | 12,04 |
| 22 | 264 | 1 | 265 | 13,278 |
| 32 | 384 | 1 | 385 | 19,621 |
| 42 | 504 | 1 | 505 | 22,472 |
| 52 | 624 | 1 | 625 | 25 |
| 62 | 744 | 1 | 745 | 27,294 |
| 72 | 854 | 1 | 855 | 29,240 |
| 82 | 984 | 1 | 985 | 31,384 |
| 92 | 1104 | 1 | 1105 | 32,241 |
| www.osfantasticosnúmerosprimos.com.br | ||||
Determinados Múltiplos de 12 de finais 8 somados com 1 unidade têm como resultados números ímpares de finais 9 e entre eles números quadrados perfeitos cujas raízes quadradas apresentam números primos.
7, 13, 17, 23, 37, 43, 47,... são números primos.
| múltiplos | ||||
|---|---|---|---|---|
| posição | de | 1 | raiz | |
| ordem | 12 | unidade | soma | quadrada |
| 4 | 48 | 1 | 49 | 7 |
| 14 | 168 | 1 | 169 | 13 |
| 24 | 288 | 1 | 289 | 17 |
| 34 | 408 | 1 | 409 | |
| 44 | 528 | 1 | 529 | 23 |
| 54 | 648 | 1 | 649 | |
| 64 | 768 | 1 | 769 | |
| 74 | 888 | 1 | 889 | |
| 84 | 1008 | 1 | 1009 | |
| 94 | 1128 | 1 | 1129 | |
| 104 | ||||
| 114 | 1368 | 1 | 1369 | 37 |
| 154 | 1848 | 1 | 1849 | 43 |
| 184 | 2208 | 1 | 2209 | 47 |
| www.osfantasticosnúmerosprimos.com.br | ||||
Determinados Múltiplos de 12 de finais 0 somados com 1 unidade têm como resultados números ímpares de finais 1 e entre eles números quadrados perfeitos cujas raízes quadradas apresentam números primos.
11, 19, 29, 31, 41,... são números primos.
| múltiplos | ||||
|---|---|---|---|---|
| posição | de | 1 | raiz | |
| ordem | 12 | unidade | soma | quadrada |
| 10 | 120 | 1 | 121 | 11 |
| 20 | 240 | 1 | 241 | |
| 30 | 360 | 1 | 361 | 19 |
| 40 | 480 | 1 | 481 | |
| 50 | 600 | 1 | 601 | |
| 60 | 720 | 1 | 721 | |
| 70 | 840 | 1 | 841 | 29 |
| 80 | 960 | 1 | 961 | 31 |
| 90 | ||||
| 100 | ||||
| 110 | ||||
| 120 | ||||
| 130 | ||||
| 140 | 1680 | 1681 | 1 | 41 |
| www.osfantasticosnúmerosprimos.com.br | ||||
Potências de base 5 elevadas a expoentes pares, igual ou maior que 2, subtraídas 1 unidade têm como resultados múltiplos de 12.
50 = 1
51 = 5
52 = 25
25 - 1 = 24 (múltiplo de 12)
53 = 125
54 = 625
625 - 1 = 624 (múltiplo de 12)
55 = 3125
56 = 16.625
16.625 - 1 = 16.624 (múltiplo de 12)
Potências de base 7 elevadas a expoentes pares, igual ou maior que 2, subtraídas 1 unidade têm como resultados múltiplos de 12.
70 = 1
71 = 7
72 = 49
49 - 1 = 48 (múltiplo de 12)
73 = 343
74 = 2401
2401 - 1 = 2400 (múltiplo de 12)
75 = 16.807
76 = 117.649
117.649 - 1 = 117.648 (múltiplo de 12)
Potências de base 3 elevadas a expoentes pares, igual ou maior que 2, subtraídas 1 unidade não têm como resultados múltiplos de 12.
Observação importante: potências de base 3, bem como múltiplos ímpares de 3: 9, 15, 21, 33, 39, 51, 57, 69, 87, etc. e suas potências subtraídas 1 unidade não geram múltiplos de 12.
30 = 1
31 = 3
32 = 9
9 - 1 = 8 (não é múltiplo de 12)
33 = 27
34 = 81
81 - 1 = 80 (não é múltiplo de 12)
35 = 243
36 = 729
729 - 1 = 728 (não é múltiplo de 12)
Potências de base 9 elevadas a expoentes pares, igual ou maior que 2, subtraídas 1 unidade não têm como resultados múltiplos de 12.
Observação importante: potências de base 3, bem como múltiplos ímpares de 3: 9, 15, 21, 33, 39, 51, 57, 69, 87, etc. e suas potências subtraídas 1 unidade não geram múltiplos de 12.
90 = 1
91 = 9
92 = 81
81 - 1 = 80 (não é múltiplo de 12)
93 = 729
94 = 6.561
6.561 - 1 = 6.560 (não é múltiplo de 12)
95 = 59.049
96 = 531.441
531.441 - 1 = 531.440 (não é múltiplo de 12)
Autor: Ricardo Silva - março/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

NOVO LIVRO DIGITAL:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato