


Triângulos Retângulos Pitagóricos apresentam diversas propriedades algébricas, numéricas, métricas e trigonométricas e além disso são triângulos retângulos formados por sequências de 3 números inteiros que tem estreita relação com o Teorema de Pitágoras: a 2 = b 2 + c 2, onde "A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa" ou "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos".
Sequências de 3 números inteiros que são as medidas dos lados de um triângulo retângulo são denominados de Ternos Pitágoricos, Trinca Pitagórica, Ternas Pitagóricas.
Um Triângulo Retângulo Pitagórico especial é o famoso triângulo retângulo 3-4-5, isto porque, é o primeiro Triângulo Retângulo Pitagórico formado por uma sequência de 3 números inteiros consecutivos.
Pelo método usual, a partir de duas medidas é possível saber a medida do terceiro lado, assim como as projeções dos catetos e altura relativa à hipotenusa em triângulos retângulos.
Mas também é possível a partir de um número ímpar igual ou maior que 3 determinar as medidas dos lados de um triângulo retângulo pitagórico cujas medidas são formadas por ternos pitagóricos primitivos e a partir destes formarem séries de triângulos retângulos derivados.
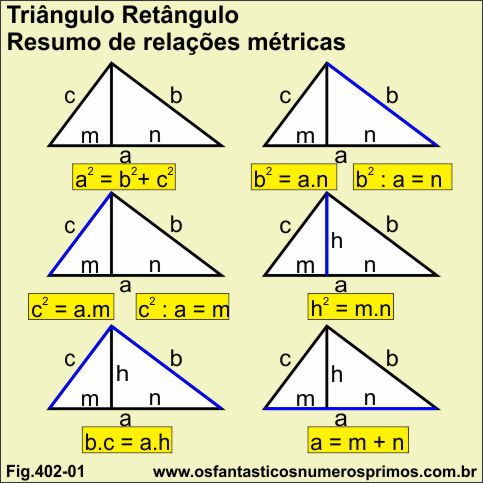
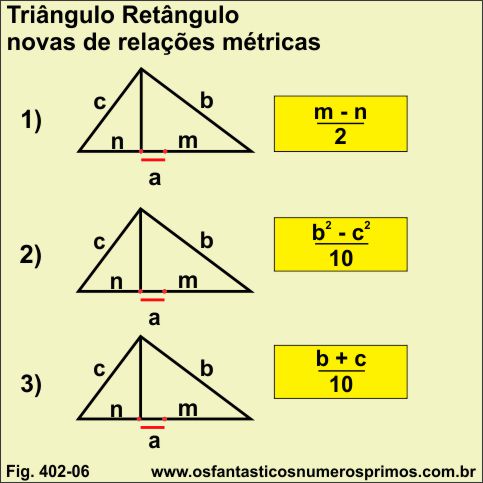
A ilustração abaixo demonstra fórmulas com as relações métricas em triângulo retângulo escaleno.
Assim como o triângulo retângulo pitagórico 15-20-25, há muitos outros triângulos com as mesmas características de terem medidas em números inteiros das projeções dos catetos e da altura relativa à hipotenusa.
Esse fato se constata com a tabulação de ternos pitagóricos derivados do Terno Pitagórico 3-4-5.
Os ternos derivados do Terno Pitagórico 3-4-5 que são múltiplos de 5 são os que apresentam as projeções dos catetos e a altura relativa à hipotenusa em números inteiros.
| Ternos Pitagóricos | ||||
| Derivados | ||||
| do Terno 3-4-5 | ||||
| Terno Primitivo | ||||
| 3 | 4 | 5 | ||
| Números | Ternos Derivados | |||
| Naturais | ||||
| c | b | a | ||
| 2 | x | 6 | 8 | 10 |
| 3 | x | 9 | 12 | 15 |
| 4 | x | 12 | 16 | 20 |
| 5 | x | 15 | 20 | 25 |
| 6 | x | 18 | 24 | 30 |
| 7 | x | 21 | 28 | 35 |
| 8 | x | 24 | 32 | 40 |
| 9 | x | 27 | 36 | 45 |
| 10 | x | 30 | 40 | 50 |
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | x | 45 | 60 | 75 |
| 16 | ||||
| 17 | ||||
| 18 | ||||
| 19 | ||||
| 20 | x | 60 | 80 | 100 |
| 21 | ||||
| 22 | ||||
| 23 | ||||
| 24 | ||||
| 25 | x | 75 | 100 | 125 |
| www.osfantasticosnumerosprimos.com.br | ||||
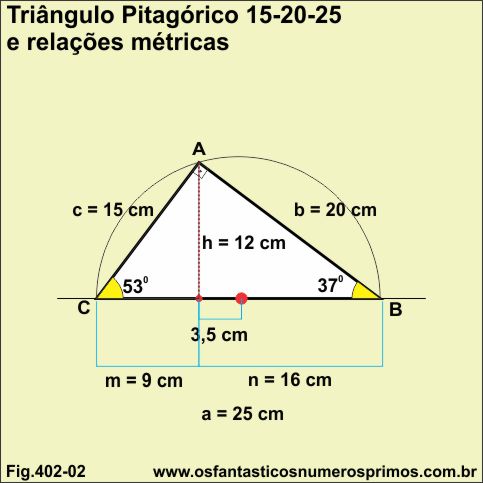
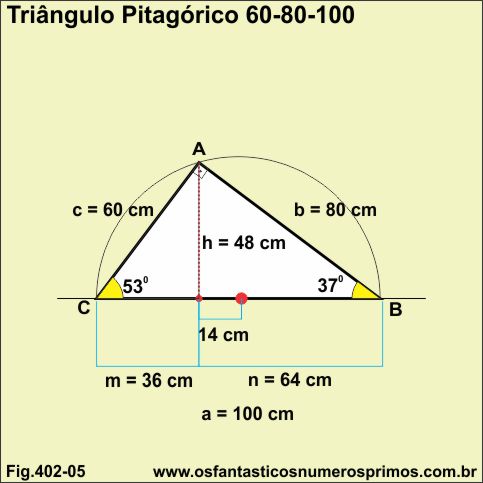
O triângulo retângulo pitagórico 15-20-25 é o primeiro triângulo retângulo cujas medidas das projeções dos catetos e a altura relativa à hipotenusa são números inteiros.
Uma nova propriedade métrica constatada em triângulos retângulos pitagóricos é que:
a) a metade do quociente da diferença entre as projeções dos catetos;
b) ou a 10a parte do quociente dos quadrados dos catetos;
c) ou a 10a parte do quociente da soma dos catetos determinam a medida que corresponde ao ponto onde a bissetriz do ângulo de 90 graus intersecta a hipotenusa.
Exemplo:
Diferença entre as projeções dos catetos
16 - 9 = 7
Diferença dividida por 2
7 : 2 = 3,5
Demarcando 3,5 cm a partir do ponto médio da hipotenusa para à esquerda, encontra-se o ponto que corresponde à altura da hipotenusa.
O mesmo ponto onde a bissetriz do ângulo de 90 graus intersecta com a hipotenusa.
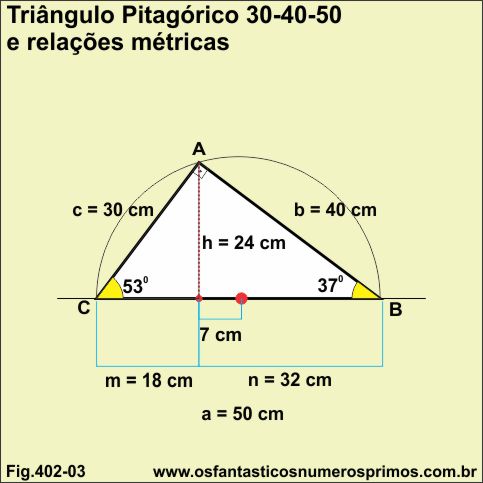
Diferença entre as projeções dos catetos
32 - 18 = 14
Diferença dividida por 2
14 : 2 = 7
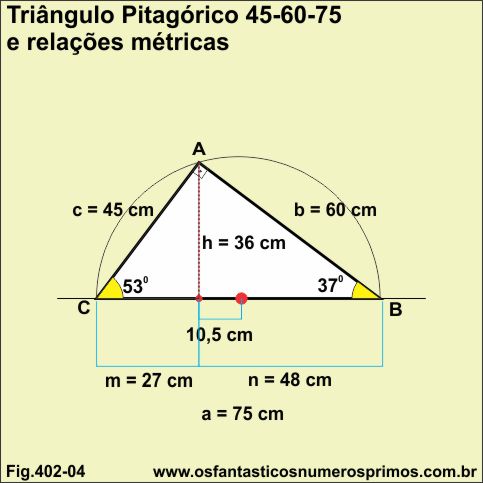
Diferença entre as projeções dos catetos
48 - 27 = 21
Diferença dividida por 2
21 : 2 = 10,5
Diferença entre as projeções dos catetos
48 - 27 = 21
Diferença dividida por 2
21 : 2 = 10,5
Interessante observar que as diferenças entre as projeções dos catetos são múltiplos de 7: 7, 14, 21, ...
7 é a soma dos termos 3 e 4 do Terno Pitagórico Primitivo 3-4-5.
Os estudos com ternos pitagóricos, bem como, com triângulos retângulos pitagóricos propiciaram deduzir novas fórmulas para se saber a medida que parte do ponto médio da hipotenusa para à esquerda e assim determinar um outro ponto que corresponde a altura relativa à hipotenusa sem necessariamente ter que determinar as medidas das projeções dos catetos sobre à hipotenusa utilizando por exemplo as fórmulas 2 e 3 (Fig.402-06)
Autor: Ricardo Silva - setembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato