


A Quadratura do Círculo é um clássico problema geométrico grego que consiste em construir um quadrado de mesma área a de um círculo dado: lado2 = Π.r2
Um problema geométrico que tem desafiado grandes matemáticos, entusiastas matemáticos, estudiosos, etc..., isto porque, o problema deve ser resolvido com compasso e régua não graduada.
Louis Ferdinand von Lindemann (1852-1939), matemático alemão, declarou ser ímpossível em 1882 construir um quadrado de mesma área que um círculo com apenas régua e compasso. Ele provou que Π (pi) é número transcendente.
Bert Janssen nasceu na Holanda, é agrônomo, matemático, escritor, contador de histórias, palestrante e estudioso de geometria sagrada e crop cicles (agroglifos, círculos em plantações).
Em seu WebSite:
https://www.cropcirclesandmore.com/,
Bert Janssen divulga parte de seus trabalhos e de suas histórias, em um de seus artigos: Squaring the Circle - a clarification (Quadratura do Círculo - um esclarecimento), publicado em 2012, ele comenta que recebera muitos e-mails em que os remetentes afirmaram que ele estava errado, que ele deveria usar em seus estudos a Quadratura do Círculo em função da área do circulo e do quadrado e não em função da circunferência, isto é, dos perímetros do círculo e do quadrado.
Deixo um convite, a você, estimado visitante, para ver o referido artigo:
https://
e tirar a suas conclusões.
Neste estudo são apresentados métodos de construções da Quadratura do Círculo em funções de áreas e perímetros e também por métodos numéricos aproximados.
O estudo faz análises construtivas da Quadratura do Círculo por meio de malhas quadriculadas e de polígonos sobrescritos em circunferências demonstrando que os métodos e técnicas utilizando-se de compasso e régua não graduada são quase imperceptíveis a olho nu.
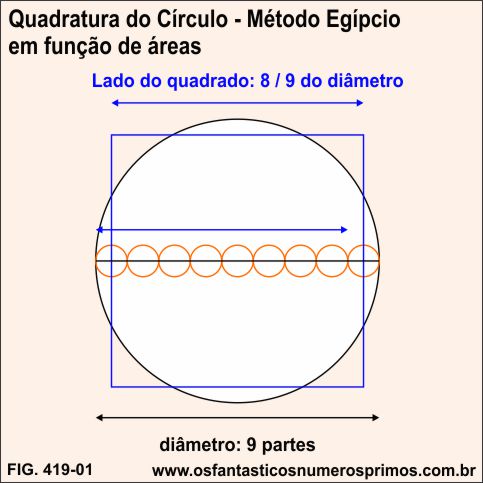
Por volta de 1800 a.C., os Egípcios criaram um método para quadrar um círculo:
a) dividi-se o diâmento do círculo em 9 partes (circunferências de cor laranja);
b) constrói-se um quadrado cujo lado seja 8 partes do diâmetro do círculo, centralizando-o no próprio círculo.
Fonte: fórmula adaptada de Dante, Luiz Roberto. Tudo é Matemática. 90 ano.
i)
| 8 | ||||
| Lado | = | ___ | x | diâmetro |
| 9 |
ii)
| 8 | ||||
| Lado | = | ___ | x | 2 x raio |
| 9 |
iii)
| 16 | ||||
| Lado | = | ___ | x | raio |
| 9 |
iv)
| Lado | = | 1,777.... | x | raio |
v)
Considerando: medida do diâmetro 1 unidade e raio 0,5 unidade...
| Lado | = | 1,777.... | x | 0,5 |
vi)
O lado do quadrado é 0,888...unidades.
| Lado | = | 0,888... |
área do círculo 0,52 x 3,14 = 0,785398
área do quadrado = 0,8882 = 0,788544
Fonte: fórmula adaptada de Dante, Luiz Roberto. Tudo é Matemática. 90 ano.
i)
| Lado2 | = | Π x r2 |
ii)
| Lado | = | √ Π x r2 |
iii)
| Lado | = | r √ Π |
iv)
Considerando: medida do diâmetro 1 unidade e raio 0,5 unidade e Π (pi) 3,14...
| Lado | = | 0,5 x 1,772... |
v)
O lado do quadrado é 0,886...unidades.
| Lado | = | 0,886... |
área do círculo 0,52 x 3,14 = 0,785398
área do quadrado = 0,8862 = 0,784996
Neste exemplo o quadrado possui lado de 7/9 do diâmetro do círculo.
7 / 9 = 0,777...
0,777 x 2 x raio =
= 0,777 x 2 x 0,5
= 0,777
Perímetro do círculo (circunferência)
diâmetro x Π (pi)
1 x 3,1415 = 3,14
Perímetro do quadrado
Lado x 4
0,777 x 4 = 3,11
Veja que no Método Egípcio, a diferença entre os perímetros do círculo e do quadrado é de 3 centésimos.
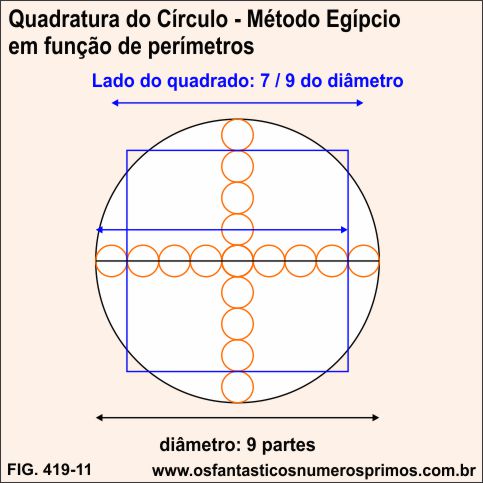
A diferença entre o perímetro do círculo e do quadrado na Quadratura do Círculo em função de áreas é significativa.
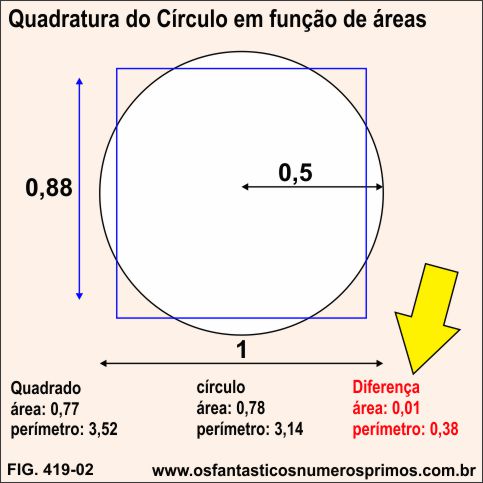
A diferença entre a área do círculo e do quadrado na Quadratura do Círculo em função de áreas, podemos dizer, que é quase imperceptível, bastante interessante, diferença de 1 centésimo.
Observação importante: neste exemplo a medida do lado do quadrado foi obtida por aproximações numéricas e se chegou a 0,88.
Extraindo-se a raiz quadrada dá área da círculo, obtem-se também 0,88 correspondente ao lado do quadrado:
√0,78 = 0,88
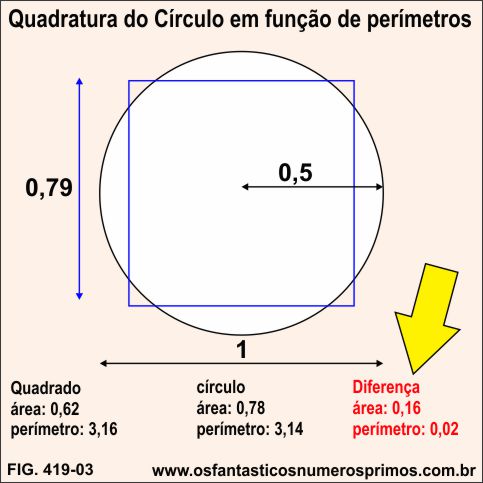
A diferença entre a área do círculo e do quadrado na Quadratura do Círculo em função de perímentos é bem significativa.
A diferença entre o perímetro do círculo e do quadrado na Quadratura do Círculo em função de perímentos, podemos dizer, também, que é quase imperceptível, bastante interessante, diferença de 2 centésimos.
Observação importante: neste exemplo a medida do lado do quadrado foi obtida por aproximações numéricas e se chegou a 0,79.
Traçando-se uma malha quadriculada de 4x4 células na quadratura do círculo - Método Egípcio, as intersecções dos vértices das células dos cantos do quadrado com o círculo são quase perfeitas.
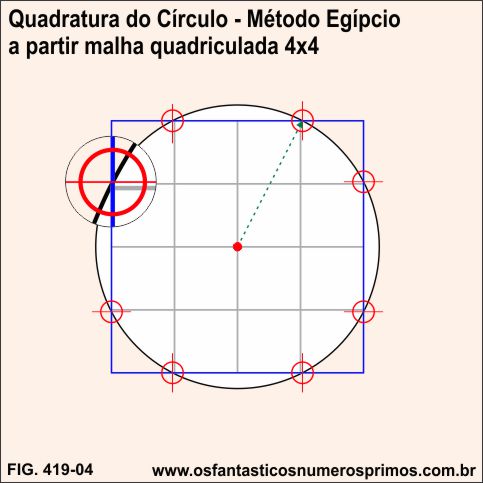
Sobrescrevendo um polígono de 20 lados (icoságono) na quadratura do círculo - Método Egípcio, 8 pontos médios de 8 de seus lados intersectam quase que perfeitamente o círculo e o quadrado (imperceptível a olho nu).
Trançando-se 2 raios até as intersecções no primeiro quadrante, os ângulos formados são 27 e 63 graus respectivamente.
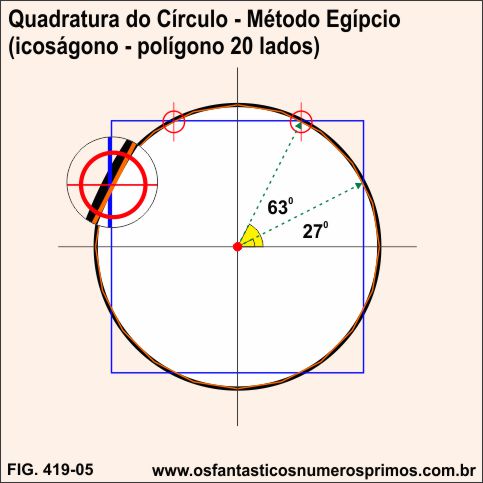
Traçando-se uma malha quadriculada de 9x9 células na quadratura do círculo em função de áreas, as intersecções dos vértices das células do quadrado sobre o círculo são quase perfeitas.
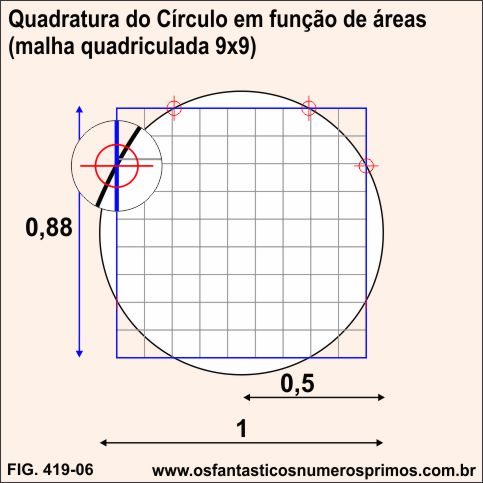
Sobrescrevendo um polígono de 32 lados (dotriacontágono) na quadratura do círculo em função de áreas, 8 pontos médios de 8 de seus lados intersectam o círculo e o quadrado.
Trançando-se 2 raios até as intersecções no primeiro quadrante, os ângulos formados são 28 e 62 graus respectivamente.
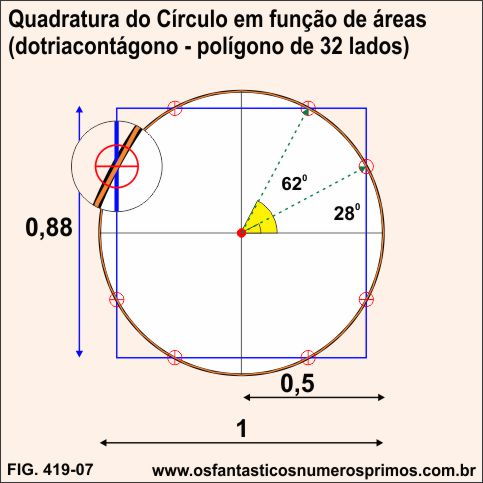
Traçando-se uma malha quadriculada de 8x8 células na quadratura do círculo em função de perímetros, as intersecções dos vértices das células do cantos do quadrado são quase perfeitas sobre o círculo.
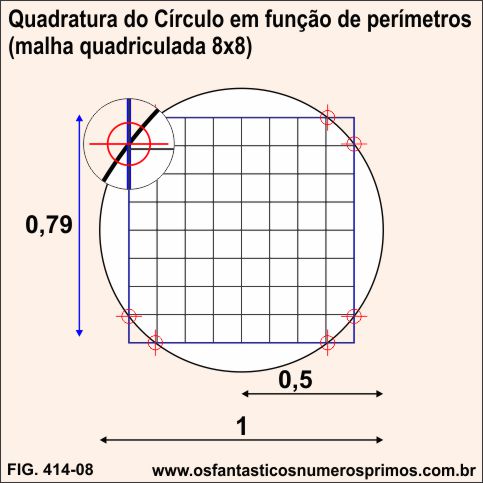
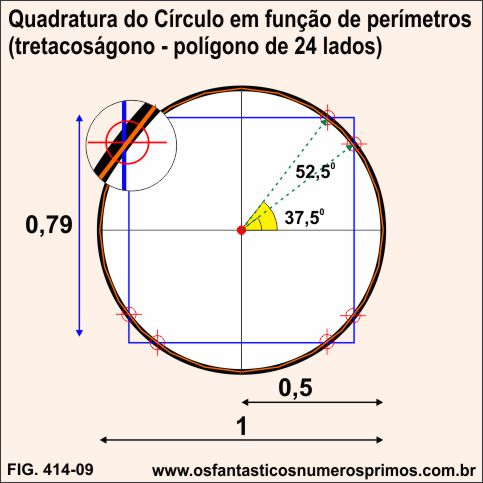
Sobrescrevendo um polígono de 24 lados (tetracoságono) na quadratura do círculo em função de perímetros, 8 pontos médios de 8 de seus lados intersectam perfeitamente o círculo e o quadrado.
Trançando-se 2 raios até as intersecções no primeiro quadrante, os ângulos formados são aproximadamente 37,5 e 52,5 graus respectivamente, ângulos estes que se relacionam a Triângulo Retângulo Pitagórico.
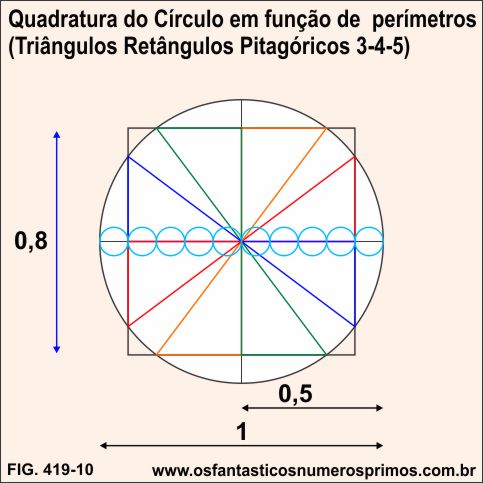
Dividindo-se o diâmetro do círculo em 10 partes (circunferências cor azul) e tomando 8 partes para o lado do quadrado e este centralizado no círculo, constrói-se a Quadradura do Círculo em função de perímetros semelhante a Quadratura do Círculo pelo Método Egípcio.
Interessante observar nesta construção geométrica que:
a) é póssivel inscrever 8 Triângulos Retângulos Pitagóricos 3-4-5 rotacionados;
b) os catetos maior tangenciam os diâmetros vertical e o horizontal;
c) os catetos menor tangenciam os lados do quadrado;
d) os ângulos agudos de maior grau dos triângulos retângulos intersectam o quadrado e o círculo simultaneamente formando um todo simétrico e harmonioso.
Efetuando-se os cálculos:
Perímetro do círculo (circunferência)
diâmetro x Π (pi)
1 x 3,14 = 3,14
Perímetro do quadrado
Lado x 4
0,8 x 4 = 3,20
diferença de 6 centésimos
Tem-se nesta construção geométrica mais uma propriedade relacionada a Triângulo Retângulo Pitagórico de que é possível construir a Quadratura do Círculo em função de perímetros.
Autor: Ricardo Silva - janeiro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://www.cropcirclesandmore.com/
https://

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato