


O Papiro de Rhind, também denominado de Papiro de Amósis é um documento egípcio de aproximadamente de 1.650 a.C. que contêm diversos problemas de aritmética, frações, geometria, etc... o qual foi adquirido por Alexander Henry Rhind, de Aberdeen (Escócia), em 1858, em Luxor, no Egito. Atualmente o papiro se encontra no Museu Britânico.
Na parte segunda do papiro (Livro II) encontra-se problemas de geometria e entre eles os problemas de números 48 e 50 os quais os egípcios chegaram ao valor 3,1604938..., número este bem próximo ao número Π (pi) 3,14159265... e também cálculos de como construir um quadrado de mesma área de um círculo, denominado de Quadratura do Círculo.
Para mais informações, veja matérias relacionadas abaixo.
A construção de um quadrado de mesma área de um círculo dado, chegou ao mundo grego, e mesmo com exímios estudiosos e pensadores, não conseguiram obter solução para o tal problema geométrico.
Matématicos de renome e entusiastas matemáticos também tentaram uma solução para o problema, até que em 1882, Louis Ferdinand von Lindemann (1852-1939), matemático alemão, declarou ser ímpossível construir um quadrado de mesma área a de uma círculo com régua não graduada e compasso. Ele provou que Π (pi) é número transcendente.
Mesmo sendo ímpossível de se construir um quadrado de mesma área de um círculo, a Quadratura do Círculo revela extraordinárias conexões matemáticas, geométricas e numéricas, por exemplo, com a inclinação de 23,5 graus da Terra, com figuras geométricas como as do pentágono e pentagrama, etc...
Para mais informações, veja matérias relacionadas abaixo.
Os estudos a seguir tem como referência a Quadratura do Círculo - Método Egípcio - em função de perímetros.
Para mais informações, veja matérias relacionadas abaixo.
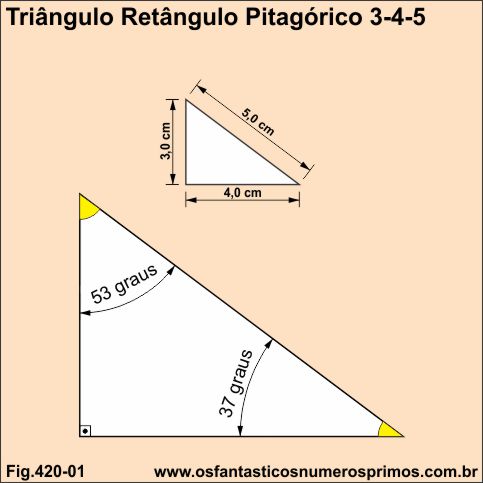
O triângulo retângulo de lados 3, 4, 5 é um triângulo retângulo especial, um triângulo milenar, pois, já era utilizado pelos antigos mesopotâmios, egípicios, chineses, etc... É o primeiro triângulo retângulo formado por números inteiros consecutivos, isto é, uma progressão aritmética, e que se relaciona com o Teorema de Pitágoras: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a² = b² + c²
5² = 4² + 3²
25 = 16 + 9
25 = 25
Os seus ângulos agudos, desprezando-se as casas decimais, são 37 e 53 graus, dois ângulos cujos números são primos.
Estas são algumas entre diversas outras propriedades relacionadas ao Triângulo Retângulo Pitagórico 3-4-5.
Dividindo-se o diâmetro do círculo em 10 partes (circunferências cor azul) e tomando-se 8 partes para o lado do quadrado e este centralizado no círculo, constrói-se a Quadradura do Círculo em função de perímetros semelhante a Quadratura do Círculo pelo Método Egípcio.
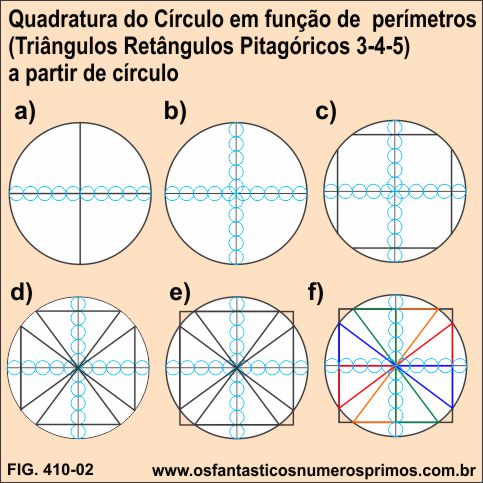
a) a partir de 2 retas perpendiculares, constrói-se um círculo e divide-se o diâmetro horizontal em 10 partes;
b) dividi-se o o diâmetro vertical em 10 partes;
c) a partir do centro, conta-se 4 unidades e traçam-se 4 cordas, duas paralelas ao eixo horizontal e duas paralelas ao eixo vertical;
d) une-se os extremos das cordas com os extremos opostos da cordas opostas;
e) completa-se o quadrado;
f) forma-se a Quadratura do Círculo em função de perímetros com Triângulos Retângulos Pitagóricos.
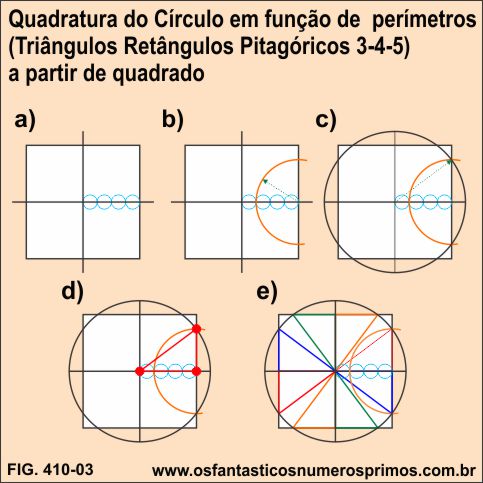
a) a partir de 2 retas perpendiculares e um quadrado, divide a metade do quadrado em 4 partes (circunferências cor azul);
b) traça-se um arco (cor laranja) de 3/4 da metade do quadrado com centro no ponto médio do lado direito do quadrado;
c) a partir do centro, traça-se uma circunferência cujo raio intersecta o arco com o lado direito do quadrado;
d) unindo os pontos (cor vermelho) com seguimentos de retas, forma-se um Triângulo Retângulo Pitagórico 3-4-5;
e) traçando-se raios até as intersecções do quadrado como o círculo, formam-se 8 Triângulos Retângulos Pitagóricos 3-4-5.
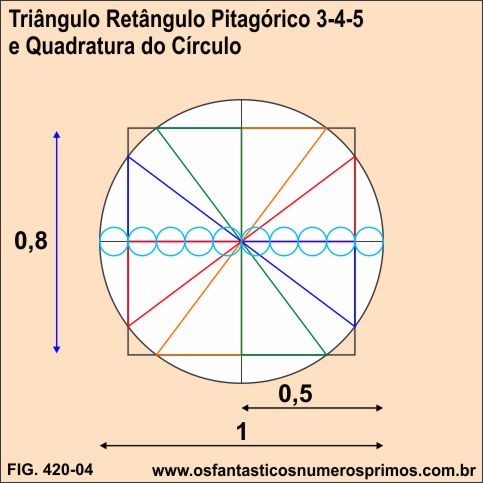
Interessante observar nas construções geométricas que:
a) são póssíveis de se inscreverem 8 Triângulos Retângulos Pitagóricos 3-4-5 rotacionados;
b) os catetos maior tangenciam os diâmetros vertical e horizontal, bem como, as retas perpendiculares;
c) os catetos menor tangenciam os lados do quadrado;
d) os ângulos agudos de maior grau dos triângulos retângulos intersectam o quadrado e o círculo simultaneamente, formando um todo simétrico e harmonioso.
Efetuando-se os cálculos:
Fonte: fórmula adaptada de Dante, Luiz Roberto. Tudo é Matemática. 90 ano.
i)
| 8 | ||||
| Lado | = | ___ | x | diâmetro |
| 10 |
ii)
| 8 | ||||
| Lado | = | ___ | x | 2 x raio |
| 10 |
iii)
| 16 | ||||
| Lado | = | ___ | x | raio |
| 10 |
iv)
| Lado | = | 1,6 | x | raio |
Interessante observar que 1,6 é Número Phi (Ф), o Número de Ouro (arredondado).
v)
Considerando: medida do diâmetro 1 unidade e raio 0,5 unidade...
| Lado | = | 1,6 | x | 0,5 |
vi)
O lado do quadrado é 0,8 unidades.
| Lado | = | 0,8 |
Perímetro do círculo (circunferência)
diâmetro x Π (pi)
1 x 3,14 = 3,14
Perímetro do quadrado
Lado x 4
0,8 x 4 = 3,20
diferença de 6 centésimos
Tem-se nestas construções geométricas mais uma propriedade relacionada a Triângulo Retângulo Pitagórico de que é possível construir a Quadratura do Círculo em função de perímetros.
Aqui uma curiosidade: a cruz pátea (derivada do francês croix pattée significando cruz patada), por vezes chamada cruz templária, e na maioria das vezes apelidada de cruz de Malta.
Uma das variantes dessas cruzes é a com pontas triangulares peenchendo quase todo o espaço quadrangular.
Interessante observar que a Cruz Pátea Triangular se assemelha a cruz formada por Triângulos Retângulos Pitagóricos 3-4-5 na Quadratura do Círculo em função de perímetros.

Autor: Ricardo Silva - janeiro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/wiki,

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato