


Todo Triângulo inscrito numa semicircunferência é um triângulo retângulo.
O triângulo retângulo de ângulo de 30, 60 e 90 graus quando inscrito numa semicircunferência se encaixa perfeitamente na forma da "meia-lua" que é formada pela própria semicircunferência.
O vértice do ângulo de 90 graus e o seguimento da altura relativa à hipotenusa se encontram justamente na intersecção com a semicircunferência.
O seguimento da altura relativa à hipotenusa, parte do ponto médio do raio da semicircunferência até um ponto da própria semicircunferência.
Propriedades estas, que não acontecem com triângulos cujos ângulos diferem de 30 e 60 graus.
Os ângulos do triângulo retângulo de 30, 60 e 90 graus são submúltiplos do número 360.
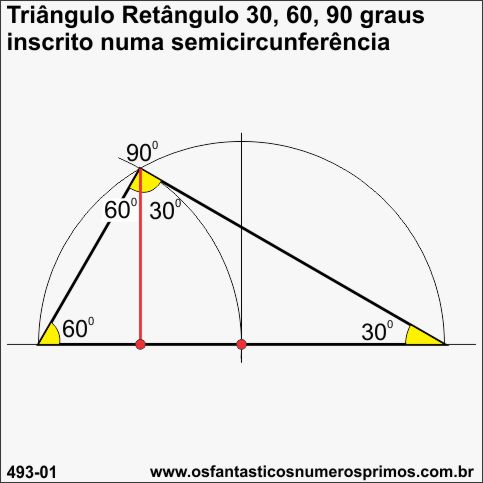
Outra propriedade intrínsica de um triângulo retângulo de 30, 60 e 90 graus e que a razão entre a medida do cateto oposto pela hipotenusa é constante, isto é, vale 1/2, denominada de seno de 30 graus.
A medida do cateto oposto é a metade da medida da hipotenusa, ou a medida da hipotenusa é o dobro da medida do cateto oposto.
Para se construir triângulo retângulo de 30 - 60 - 90 graus cuja base é a hipotenusa procedemos assim:
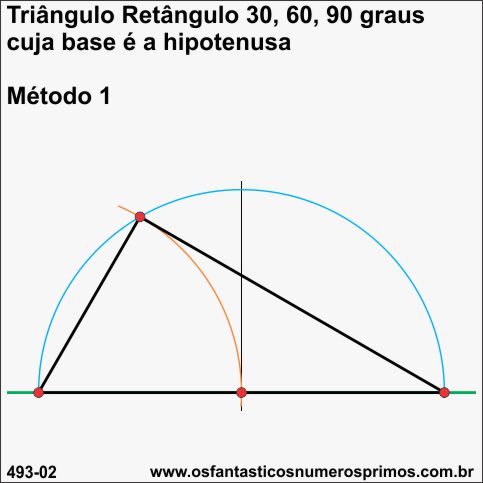
1) sobre uma reta, traça-se uma semicircunfêrencia;
2) com o compasso, centro na extremidade esquerda do diâmetro e abertura no ponto médio da semicircunfêrencia, traça-se um arco intersectando a semicircunfêrencia;
3) unindo os pontos das extremidades do diâmetro com o ponto na semicircunfêrencia, obtem-se triângulo retângulo de 30 - 60 - 90 graus.
Para se construir triângulo retângulo de 30 - 60 - 90 graus cuja base é a hipotenusa e de comprimento determinado, procedemos assim:
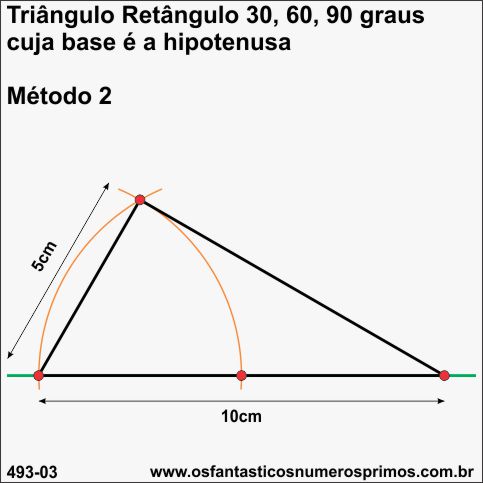
1) traça-se uma reta de comprimento desejado, por exemplo, 10cm;
2) marque o ponto médio da reta (10 / 2 = 5cm);
3) centro na extreminade esquerda da reta e abertura no ponto médio, traça-se um arco de circunferência;
4) com a mesma abertura do compasso, centro no ponto médio da reta, traça outro arco, desta forma, tem-se o ponto de intersecção dos dois arcos;
5) unindo-se as extremidades da reta com a intersecção dos arcos de circunferências, obtem-se triângulo retângulo de 30 - 60 - 90 graus de hipotenusa medindo 10cm e cateto menor medindo 5cm.
Para se construir triângulo retângulo de 30 - 60 - 90 graus cuja base é o cateto maior procedemos assim:
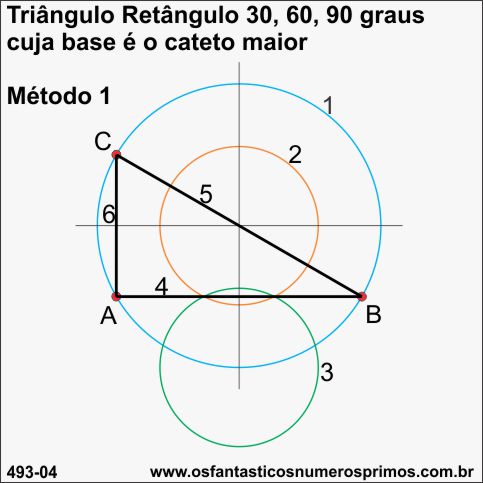
1) no cruzamento das retas perpendiculares, traçar a circunferência (1);
2) no cruzamento das retas perpendiculares, traçar a circunferência (2) cujo raio seja a metade do raio da circunferência maior (1);
3) no cruzamento a circunferência (1) com a reta vertical, traçar outra circunferência (3) cujo raio seja a metade do raio da circunferência maior (1);
4) traçar um seguimento de reta passando pelos pontos de intersecções das circunferências menores (2) e (3) e marcar os ponto A a B na circunferência maior (1);
5) partindo-se do ponto B e passando pelo centro da circunferência maior (1), traçar seguimento de reta e marcar o ponto C na circunferência (1);
6) partindo-se do ponto C, traçar um segmento de reta até o ponto A.
7) unindo os pontos A, B e C forma-se um triângulo retângulo de 30 - 60 - 90 graus.
Observações:
a) Neste exemplo de construção, a medida do diâmetro é a mesma da hipotenusa e cateto maior (base) fica paralelo ao diâmetro horizontal formado pelas retas perpendiculares;
b) as circunferências menores ficam alinhadas verticalmente.
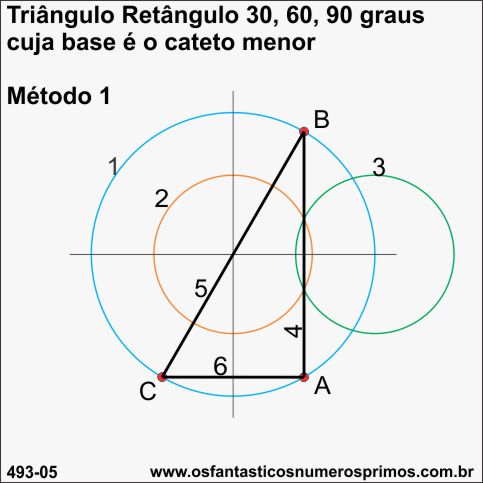
Para se construir triângulo retângulo de 30 - 60 - 90 graus cuja base é o cateto menor, podemos utilizar o Método 1 para construção de triângulo retângulo de 30 - 60 - 90 graus cuja base é o cateto maior.
Observações:
a) neste exemplo de construção, a medida do diâmetro é a mesma da hipotenusa e cateto menor (base) fica paralelo ao diâmetro horizontal formado pelas retas perpendiculares.
b) as circunferências menores ficam alinhadas horizontalmente.
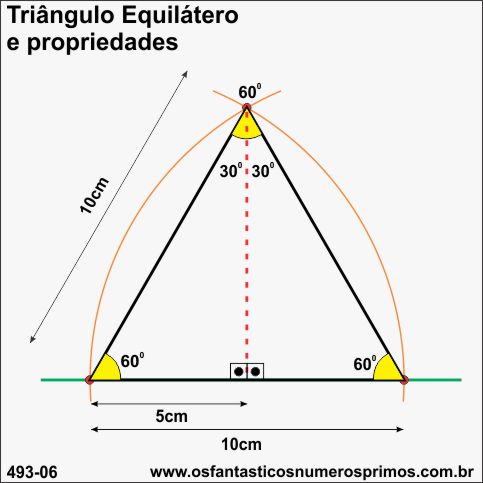
Triângulo Equilátero é um polígono regular de 3 lados com mesmas medidas e também os três ângulos agudos de 60 graus.
Trançando-se a sua altura a partir do ponto médio de um de seus lados, obtêm-se dois triângulos retângulos de 30 - 60 - 90 graus.
Interessante observar no triângulo equilátero que se o lado (base) tiver medida de número inteiro par, então os triângulos retângulos de 30 - 60 - 90 inscritos terão as medidas da hipotenusa e do cateto menor também um número inteiro.
Para se construir um triângulo equilátero, procedemos assim:
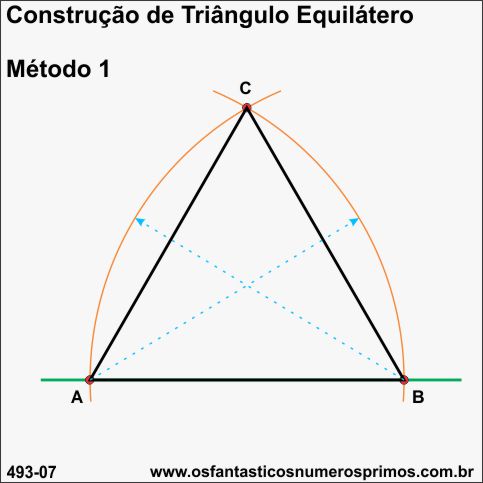
1) sobre uma reta, marcam-se os pontos A e B;
2) centro em A e abertura em B, traçar um arco de circunferência;
3) centro em B e abertura em A, traçar outro arco de circunferência;
3) na intersecção dos dois arcos, marcar o ponto C;
4) unindo os pontos A, B e C tem-se um triângulo equilátero.
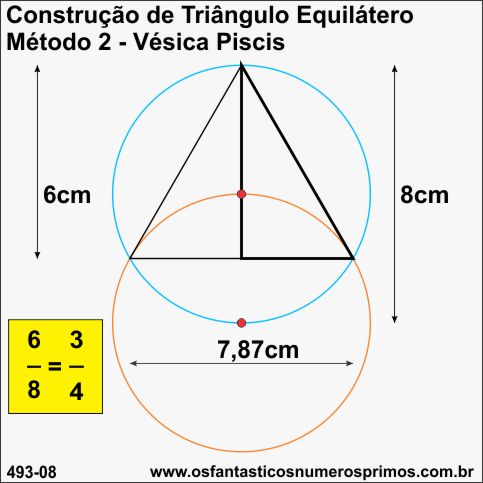
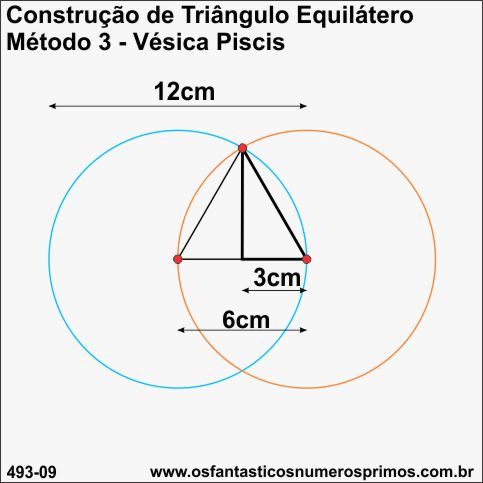
Vésica Piscis é uma construção geométrica com duas circunferências de mesmo raio na qual o centro de uma está sobre a circunferência da outra.
Por meio da Vésica Piscis são possíveis de se construirem diversas outras figuras geométricas.
Para mais informações, veja abaixo, Matérias Relacionadas.
Triângulo Equilátero construído com a Vésica Piscis (Método 2 - circunferências em sentido "vertical") têm a sua altura correspondendo a 3/4 do diâmetro da circunferência.
Interessante observar que na construção abaixo, o diâmetro da circunferência tem medida de 8cm e altura do triângulo equilâtero, bem como, o cateto maior do Triângulo Retângulo de 30-60-90 graus medidas de 6cm, ambos números inteiros.
Triângulo Equilátero construído com a Vésica Piscis (Método 3 - circunferências em sentido "horizontal") em que os diâmetros tenham como medida número inteiro par, a base do triângulo equilátero, bem como, o cateto menor do Triângulo Retângulo de 30-60-90 inscrito inscrito, terão também medidas em números inteiros.
Autor: Ricardo Silva - junho/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato