


Quadrados Mágicos são dispositivos numéricos, formados por células em quantidades de números quadrados perfeitos, nos quais:
a) dispondo sequências numéricas formadas por progressões aritméticas, em certa ordem, as somas de cada uma das linhas, cada uma das colunas, bem como, as diagonais tem como resultado um mesmo total, denominada de Constante Mágica;
b) dispondo sequências numéricas formadas por progressões geométricas ou determinados conjuntos de divisores de um número natural, em certa ordem, os produtos de cada uma das linhas, cada uma das colunas, bem como, as diagonais tem como resultado um mesmo produto, denominado de Contante Mágica.
Neste estudo é apresentado uma nova propriedade na qual são possíveis de construírem infinitos quadrados mágicos de mesmas Constantes Mágicas, propriedade esta, enviada pelo Sr. Aristóteles Costa, Entusiasta Matemático.
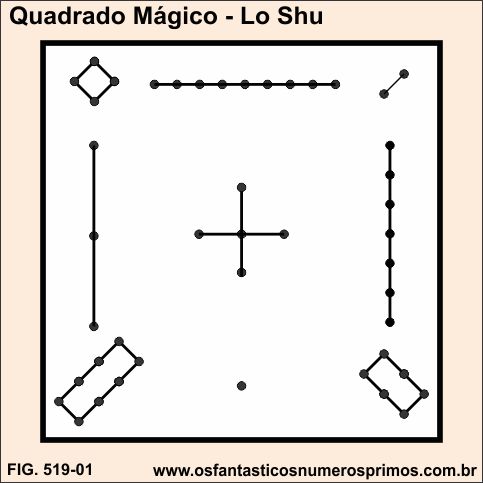
O aparecimento do Quadrado Mágico têm como origem a China, e se encontra documentado no Livro Os 9 capítulos da arte matemática no texto Shu Shu Shi Yu, baseado na estória do Imperador Yu que viu sair do Rio Lo (Rio Amarelo) uma tartaruga com marcas em formas de nós feitos em barbantes sobre seu casco.
O imperador Yu também observou que as marcas quando contadas nas horizontais, verticais e diagonais possuiam uma mesma soma, isto é, 15. A partir destes eventos a tartagura, que é um animal venerado pela sua longevidade na cultura chinesa, recebeu o nome de Lo-Shu e passou a ter carater místico e esotérico.
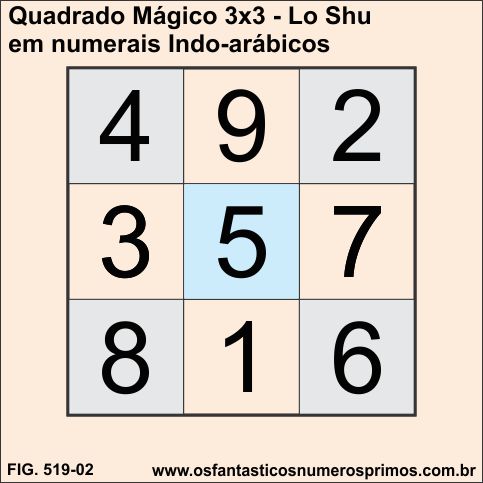
O Quadrado Mágico transcrito para o sistema de numeração indo-arábico nos permite também visualizar um "algo a mais" embutido na sua construção.
Podemos vê-lo como uma balança virtual, por exemplo, jamais poderíamos equilibrar 2 kilos de arroz com 8 quilos de arroz, mas no Quadrado Mágico há o constante equilíbrio exercido pelo número 5, ele é o eixo moderador de todos os números que o cercam.
As duplas de números com seus diferentes "pesos" formam o dobro do número central que os equilibram formando um conjunto harmonioso, pares com pares e ímpares com ímpares.
Os números são se repetem, se associam ao número central e formam uma quantidade constante que dá a magia ao quadrado.
Para cada Quadrado Mágico, temos várias combinações dependendo do tamanho da matriz, conforme a tabela a seguir. Salientamos que nem toda permutação entre os elementos de um Quadrado Mágico Perfeito gera outro Quadrado Mágico Perfeito. Se permutarmos os elementos de uma matrix 3x3, teremos 362.880 matrizes, mas apenas 8 são Quadrados Mágicos Perfeitos.
| Quantidade de Combinações | |
| Ordem | Quantidade |
| 3 (3x3) | 8 |
| 4 (4x4) | 880 |
| 5 (5x5) | 275.305.224 |
| 6 6x6) | estima-se 1, 7.1019 |
Fonte: adaptado de [1]
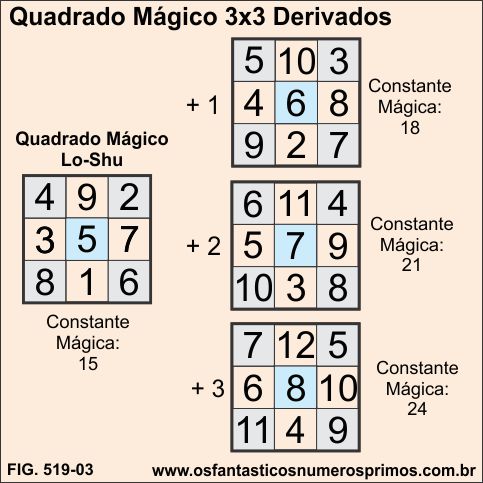
Quadrado Mágico Derivado é quando somamos ou diminuimos uma constante aos números de um Quadrado Mágico Perfeito, Normal ou Puro.
No exemplo, alguns quadrados mágicos derivados do Quadrado Mágico 3x3 Lo-Shu.
No estudo de número 176:
011-estudos-176-quadrados-magicos-e-qualquer-numero
é apresentado uma brincadeira, isto é, um passatempo de construção de quadrado mágico, onde a pessoa escolhe um número a partir do número 5 é você dirá a ela que construindo um quadrado mágico 3x3, a constante mágica é um número tal, para todas as linhas, colunas e diagonais.
Este passatempo consiste em montar uma progressão aritmética com 9 termos, neste exemplo, o número escolhido é o número 5 como termo central:
a) diminui-se sempre 1 unidade a partir do 5;
b) soma-se sempre 1 unidade a partir do 5;
| Progressão Aritmética | ||||||||
|---|---|---|---|---|---|---|---|---|
| de 1 a 9 | ||||||||
| 5 | ||||||||
| 4 | 6 | |||||||
| 3 | 7 | |||||||
| 2 | 8 | |||||||
| 1 | 9 | |||||||
Desta forma se tem uma progressão aritmética finita de 9 termos cuja a razão e primeiro termo é 1 e o termo central 5

Tendo como base o Quadrado Mágico Lo-Shu, podemos construir infinitos outros quadrados mágicos de Constantes Mágicas Iguais, tendo como termo central o número 5 e variando-se as razões:
1) razão 2
| -3 | -1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 15 | |||
| 3 | 13 | -1 | 15 |
| 1 | 5 | 9 | 15 |
| 11 | -3 | 7 | 15 |
| 15 | 15 | 15 | 15 |
2) razão 3
| -7 | -4 | -1 | 2 | 5 | 8 | 11 | 14 | 17 |
| 15 | |||
| 2 | 17 | -4 | 15 |
| -1 | 5 | 11 | 15 |
| 14 | -7 | 8 | 15 |
| 15 | 15 | 15 | 15 |
3) razão 4
| -11 | -7 | -3 | 1 | 5 | 9 | 13 | 17 | 21 |
| 15 | |||
| 1 | 21 | -7 | 15 |
| -3 | 5 | 13 | 15 |
| 17 | -11 | 9 | 15 |
| 15 | 15 | 15 | 15 |
Outro método de se contruirem quadrados mágicos de Constantes Mágicas Iguais é escolher um múltiplo de 9 e dividí-lo por 9.
819 : 9 = 91
Fixando-se o número 91 como termo central e variando-se as razões, formam-se progressões aritméticas finitas de mesmas somas.
Os quadrados mágicos construídos têm Constantes Mágicas Iguais cujo valor é 273.
1) razão 1
| 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
| 273 | |||
| 90 | 95 | 88 | 273 |
| 89 | 91 | 93 | 273 |
| 94 | 87 | 92 | 273 |
| 273 | 273 | 273 | 273 |
2) razão 2
| 83 | 85 | 87 | 89 | 91 | 93 | 95 | 97 | 99 |
| 273 | |||
| 89 | 99 | 85 | 273 |
| 87 | 91 | 95 | 273 |
| 97 | 83 | 93 | 273 |
| 273 | 273 | 273 | 273 |
3) razão 3
| 79 | 82 | 85 | 88 | 91 | 94 | 97 | 100 | 103 |
| 273 | |||
| 88 | 103 | 82 | 273 |
| 85 | 91 | 97 | 273 |
| 100 | 79 | 94 | 273 |
| 273 | 273 | 273 | 273 |
4) razão 4
| 75 | 79 | 83 | 87 | 91 | 95 | 99 | 103 | 107 |
| 273 | |||
| 87 | 107 | 79 | 273 |
| 83 | 91 | 99 | 273 |
| 103 | 75 | 95 | 273 |
| 273 | 273 | 273 | 273 |
5) razão 5
| 71 | 76 | 81 | 86 | 91 | 96 | 101 | 106 | 111 |
| 273 | |||
| 86 | 111 | 76 | 273 |
| 81 | 91 | 101 | 273 |
| 106 | 71 | 96 | 273 |
| 273 | 273 | 273 | 273 |
Autores: Ricardo Silva e Ari Costa - outubro/2024
[1] Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato