


O presente estudo demonstra que as somas de quantidades constantes de potências de um número natural têm como resultados múltiplos da soma consecutiva de potências desse mesmo número natural.
Obtêm-se potências de um número natural multiplicando-se um número natural por ele mesmo tantas vezes que se queira ou por meio da Potênciação / Exponenciação.
Exemplos por meio da multiplicação:
2 = 2
2 x 2 = 4
2 x 2 x 2 = 8
2 x 2 x 2 x 2 = 16
Exemplos por meio da Potênciação / Exponenciação
20 = 1
21 = 2
22 = 4
23 = 8
Termos de uma Potenciação / Exponenciação
2³ = 8
2: base
3: expoente
8: potência
As somas consecutivas de potências de números naturais apresentam um interessante fato matemático de que as somas não são múltiplos desses números naturais, isto é, de suas respectivas bases.
As somas consecutivas de potências de base 2 não são múltiplos da base 2.
| Potências de Base 2 | Somas | |||||||
| 1 | 1 | |||||||
| 1 | 2 | 3 | ||||||
| 1 | 2 | 4 | 7 | |||||
| 1 | 2 | 4 | 8 | 15 | ||||
| 1 | 2 | 4 | 8 | 16 | 31 | |||
| 1 | 2 | 4 | 8 | 16 | 32 | 63 | ||
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 127 | |
Observação importante: as somas consecutivas de potências de base 2 têm como resultados números que são 1 unidade menor que uma potência de base 2, estes números também são denominados de:
1) Números de Mersenne;
2) Números Quase-Potências de Base 2.
Por meio de determinadas potências de base 2, bem como, de determinados Números de Mersenne (Números Quase-Perfeitos, Números Quase-Potências de Base 2) é que se obtem Números Perfeitos.
Para mais informações, veja abaixo, matérias relacionadas!
As somas consecutivas de potências de base 3 não são múltiplos da base 3.
| Potências de Base 3 | Somas | |||||||
| 1 | 1 | |||||||
| 1 | 3 | 4 | ||||||
| 1 | 3 | 9 | 13 | |||||
| 1 | 3 | 9 | 27 | 40 | ||||
| 1 | 3 | 9 | 27 | 81 | 121 | |||
| 1 | 3 | 9 | 27 | 81 | 243 | 364 | ||
| 1 | 3 | 9 | 27 | 81 | 243 | 729 | 1093 | |
As somas consecutivas de potências de base 4 não são múltiplos da base 4.
| Potências de Base 4 | Somas | |||||||
| 1 | 1 | |||||||
| 1 | 4 | 5 | ||||||
| 1 | 4 | 16 | 21 | |||||
| 1 | 4 | 16 | 64 | 85 | ||||
| 1 | 4 | 16 | 64 | 256 | 341 | |||
| 1 | 4 | 16 | 64 | 256 | 1024 | 1365 | ||
| 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 5461 | |
As somas consecutivas de potências de base 5 não são múltiplos da base 5.
| Potências de Base 5 | Somas | |||||||
| 1 | 1 | |||||||
| 1 | 5 | 6 | ||||||
| 1 | 5 | 25 | 31 | |||||
| 1 | 5 | 25 | 125 | 156 | ||||
| 1 | 5 | 25 | 125 | 625 | 781 | |||
| 1 | 5 | 25 | 125 | 625 | 3125 | 3906 | ||
| 1 | 5 | 25 | 125 | 625 | 3125 | 15625 | 19531 | |
As somas consecutivas de potências de base 6 não são múltiplos da base 6.
| Potências de Base 6 | Somas | |||||||
| 1 | 1 | |||||||
| 1 | 6 | 7 | ||||||
| 1 | 6 | 36 | 43 | |||||
| 1 | 6 | 36 | 216 | 259 | ||||
| 1 | 6 | 36 | 216 | 1296 | 1555 | |||
| 1 | 6 | 36 | 216 | 1296 | 7776 | 9331 | ||
| 1 | 6 | 36 | 216 | 1296 | 7776 | 46656 | 55987 | |
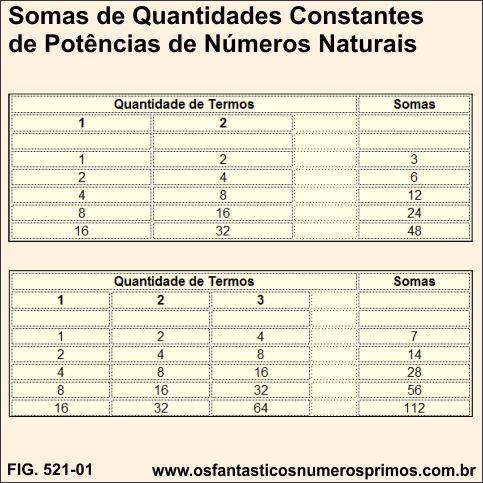
As somas consecutivas de 2 potências de base 2 têm como resultados múltiplos de 3.
3 é um Número de Mersenne.
3 é 1 unidade menor da potência 4.
| Quantidade de Termos | Somas | ||
| 1 | 2 | ||
| 1 | 2 | 3 | |
| 2 | 4 | 6 | |
| 4 | 8 | 12 | |
| 8 | 16 | 24 | |
| 16 | 32 | 48 | |
As somas consecutivas de 3 potências de base 2 têm como resultados múltiplos de 7.
7 é um Número de Mersenne.
7 é 1 unidade menor da potência 8.
| Quantidade de Termos | Somas | |||
| 1 | 2 | 3 | ||
| 1 | 2 | 4 | 7 | |
| 2 | 4 | 8 | 14 | |
| 4 | 8 | 16 | 28 | |
| 8 | 16 | 32 | 56 | |
| 16 | 32 | 64 | 112 | |
As somas consecutivas de 4 potências de base 2 têm como resultados múltiplos de 15.
15 é um Número de Mersenne.
15 é 1 unidade menor da potência 16.
| Quantidade de Termos | Somas | ||||
| 1 | 2 | 3 | 4 | ||
| 1 | 2 | 4 | 8 | 15 | |
| 2 | 4 | 8 | 16 | 30 | |
| 4 | 8 | 16 | 32 | 60 | |
| 8 | 16 | 32 | 64 | 120 | |
| 16 | 32 | 64 | 128 | 240 | |
As somas consecutivas de 5 potências de base 2 têm como resultados múltiplos de 31.
31 é um Número de Mersenne.
31 é 1 unidade menor da potência 32.
| Quantidade de Termos | Somas | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 2 | 4 | 8 | 16 | 31 | |
| 2 | 4 | 8 | 16 | 32 | 62 | |
| 4 | 8 | 16 | 32 | 64 | 124 | |
| 8 | 16 | 32 | 64 | 128 | 248 | |
| 16 | 32 | 64 | 128 | 256 | 496 | |
As somas consecutivas de 6 potências de base 2 têm como resultados múltiplos de 63.
63 é um Número de Mersenne.
63 é 1 unidade menor da potência 64.
| Quantidade de Termos | Somas | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 2 | 4 | 8 | 16 | 32 | 63 | |
| 2 | 4 | 8 | 16 | 32 | 64 | 126 | |
| 4 | 8 | 16 | 32 | 64 | 128 | 252 | |
| 8 | 16 | 32 | 64 | 128 | 256 | 504 | |
| 16 | 32 | 64 | 128 | 256 | 512 | 1008 | |
As somas consecutivas de 2 potências de base 3 têm como resultados múltiplos de 4.
| Quantidade de Termos | Somas | ||
| 1 | 2 | ||
| 1 | 3 | 4 | |
| 3 | 9 | 12 | |
| 9 | 27 | 36 | |
| 27 | 81 | 108 | |
| 81 | 243 | 324 | |
As somas consecutivas de 3 potências de base 3 têm como resultados múltiplos de 13.
| Quantidade de Termos | Somas | |||
| 1 | 2 | 3 | ||
| 1 | 3 | 9 | 13 | |
| 3 | 9 | 27 | 39 | |
| 9 | 27 | 81 | 117 | |
| 27 | 81 | 243 | 351 | |
| 81 | 243 | 729 | 1053 | |
As somas consecutivas de 4 potências de base 3 têm como resultados múltiplos de 40.
| Quantidade de Termos | Somas | ||||
| 1 | 2 | 3 | 4 | ||
| 1 | 3 | 9 | 27 | 40 | |
| 3 | 9 | 27 | 81 | 120 | |
| 9 | 27 | 81 | 243 | 360 | |
| 27 | 81 | 243 | 729 | 1080 | |
| 81 | 243 | 729 | 2187 | 3240 | |
As somas consecutivas de 5 potências de base 3 têm como resultados múltiplos de 121.
| Quantidade de Termos | Somas | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 3 | 9 | 27 | 81 | 121 | |
| 3 | 9 | 27 | 81 | 243 | 363 | |
| 9 | 27 | 81 | 243 | 729 | 1089 | |
| 27 | 81 | 243 | 729 | 2187 | 3267 | |
| 81 | 243 | 729 | 2187 | 6561 | 9801 | |
As somas consecutivas de 6 potências de base 3 têm como resultados múltiplos de 364.
| Quantidade de Termos | Somas | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 3 | 9 | 27 | 81 | 243 | 364 | |
| 3 | 9 | 27 | 81 | 243 | 729 | 1092 | |
| 9 | 27 | 81 | 243 | 729 | 2187 | 3276 | |
| 27 | 81 | 243 | 729 | 2187 | 6561 | 9828 | |
| 81 | 243 | 729 | 2187 | 6561 | 19683 | 29484 | |
Autor: Ricardo Silva - novembro/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato