Triângulo Numérico 10 - Números Quadrados Perfeitos é um dispositivo numérico infinito semelhante ao Triângulo de Pascal cuja característica principal é que cada uma de suas linhas começam e terminam com um número quadrado perfeito.
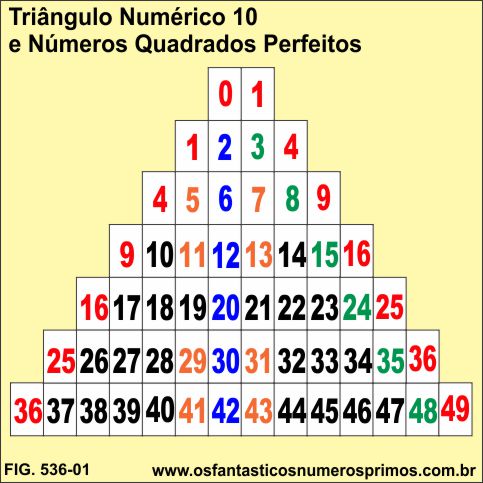
O Triângulo Numérico 10 apresenta diversas propriedades matemáticas e numéricas relacionadas a números retangulares, números primos, números primos gêmeos, bem como, com os próprios números quadrados perfeitos.
| Triângulo Numérico 10 | |||||||||||||||||||||||||
| Números Quadrado Perfeitos | |||||||||||||||||||||||||
| linha | soma | soma | soma | quociente | |||||||||||||||||||||
| termos | dos | primeiro | |||||||||||||||||||||||
| linha | intervalos | com | |||||||||||||||||||||||
| último | |||||||||||||||||||||||||
| termo | |||||||||||||||||||||||||
| (quadrados) | |||||||||||||||||||||||||
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | |||||||||||||||||||
| 1 | 1 | 2 | 3 | 4 | 10 | 5 | 5 (primo) | 1 | |||||||||||||||||
| 2 | 4 | 5 | 6 | 7 | 8 | 9 | 39 | 26 | 13 (primo) | 2 | |||||||||||||||
| 3 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 100 | 75 | 25 | 3 | |||||||||||||
| 4 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 205 | 164 | 41 (primo) | 4 | |||||||||||
| 5 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 366 | 305 | 61 (primo) | 5 | |||||||||
| 6 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 595 | 510 | 85 | 6 | |||||||
| 7 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 904 | 791 | 113 (primo) | 7 | |||||
| 8 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 1305 | 1160 | 145 | 8 | |||
| 9 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 1810 | 1629 | 181 (primo) | 9 | |
| www.osfantasticosnumerosprimos.com.br | |||||||||||||||||||||||||
O triângulo Numérico - Números Quadrados Perfeitos apresenta as seguintes propriedades numéricas:
a) cada linha começa e termina com um número quadrado perfeito (células laranjas);
b) a quantidade de termos das linhas são pares;
c) a soma dos termos da linha é múltiplo da soma do primeiro termo (quadrado) com o último termo (quadrado);
exemplos:
Linha 1
Soma dos termos: 1 + 2 + 3 + 4 = 10
Soma dos quadrados: 1 + 4 = 5
10 é múltiplo de 5.
Linha 2
Soma dos termos: 4 + 5 + 6 + 7 + 8 + 9 = 39
Soma dos quadrados: 4 + 9 = 13
39 é múltiplo de 13.
d) a soma do intervalo de cada sequência é múltiplo da
soma do primeiro termo (quadrado) com o último termo (quadrado);
exemplos:
Linha 1
Termos: 1, 2, 3, 4
Soma do intervalo: 2 + 3 = 5
Soma dos quadrados: 1 + 4 = 5
Linha 2
Termos: 4, 5, 6, 7, 8, 9
Soma do intervalo: 5 + 6 + 7 + 8 = 26
Soma dos quadrados: 4 + 9 = 13
e) a soma do intervalo dividido pela soma de 2 quadrados tem como quociente o número da linha;
exemplos:
Linha 1
5 : 5 = 1 (linha 1)
Linha 2
23 : 13 = 2 (linha 2)
Linha 3
75 : 25 = 3 (linha 3)
f) o número da linha é raiz quadrada do número quadrado perfeito que começa a própria linha.
Números retangulares são números que são produtos de 2 números consecutivos.
Números retangulares divididos por 2 têm como quocientes números triangulares.
No Triângulo Numérico 10, os números retangulares aparecem paralelos a hipotenusa (linhas azuis).
exemplos:
Linha 1
1 x 2 = 2 (número retangular)
o retangular 2 é o segundo termo
Linha 2
2 x 3 = 6 (número retangular)
o retangular 6 é o terceiro termo
Linha 3
3 x 4 = 12 (número retangular)
o retangular 12 é o quarto termo
Determinadas somas de 2 números quadrados perfeitos consecutivos têm como resultados números primos.
exemplos:
Linha 1
1 + 4 = 5
Linha 3
4 + 9 = 13
Linha 4
16 + 25 = 41
Interessante observar que o dobro de um número retangular somado 1 unidade tem como resultado a soma de 2 números quadrado perfeitos consecutivos.
Linha 1
2 + 2 + 1 = 5
soma dos quadrados 1 + 4 = 5
Linha 3
6 + 6 + 1 = 13
soma dos quadrados 4 + 9 = 13
Linha 4
20 + 20 + 1 = 41
soma dos quadrados 16 + 25 = 41
Determinados números retangulares têm como antecessores e sucessores números primos gêmeos (células verdes).
Números primos gêmeos são números cuja diferença são duas unidades.
exemplos:
Linha 2
5, 6, 7
Linha 5
29, 30, 31
Linha 6
41, 42, 43
Versão do Triângulo Numérico 10 em formato de triângulo isóceles.
| Triângulo Numérico 10 | ||||||||||||||||||||||||
| Números Quadrado Perfeitos | ||||||||||||||||||||||||
| linha | soma | soma | soma | quociente | ||||||||||||||||||||
| termos | do | primeiro | ||||||||||||||||||||||
| linha | intervalo | com | ||||||||||||||||||||||
| último | ||||||||||||||||||||||||
| termo | ||||||||||||||||||||||||
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | ||||||||||||||||||
| 1 | 1 | 2 | 3 | 4 | 10 | 0 | 5 | 1 | ||||||||||||||||
| 2 | 4 | 5 | 6 | 7 | 8 | 9 | 39 | 26 | 13 | 2 | ||||||||||||||
| 3 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 100 | 75 | 25 | 3 | ||||||||||||
| 4 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 205 | 164 | 41 | 4 | ||||||||||
| 5 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 366 | 305 | 61 | 5 | ||||||||
| 6 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 48 | 48 | 49 | 596 | 510 | 85 | 6 | ||||||
| 7 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 904 | 791 | 113 | 7 | ||||
| 8 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 1305 | 1160 | 145 | 8 | ||
| 9 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 1810 | 1629 | 181 | 9 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||||||||||||||||
Autor: Ricardo Silva e Ari Costa - janeiro/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
