


Quadrados Mágicos são dispositivos numéricos formados por matrizes quadriculadas em quantidade de números quadrados perfeitos.
Quadrados Mágicos podem ser construídos com progressões aritméticas, progressões geométricas, bem como, com determinados conjuntos de divisores de um número natural.
Conforme citação de Martin Gardner: "O Quadrado Mágico 18x18 - Número Cíclico: 052 631 578 947 368 421 foi publicado pela primeira vez no livro Magic Squares e Cubes, obra de W. S. Andrews datada de 1917 e segundo Andrews é o primeiro quadrado mágico construído com número cíclico (com algarismos de números cíclicos)" [2], o grifo é nosso.
Reiterando, o Quadrado Mágico 18x18, citado acima, foi o primeiro quadrado mágico construído com algarismos de números cíclicos alocados cada um em suas respectivas células do quadrado.
O presente estudo demonstra a construção de Quadrado Mágico 4x4 com os primeiros períodos das dízimas períodicas das frações 1/17 a 16/17, também denominadas de números cíclicos.
Número Racional é um número gerado da divisão de 2 números inteiros.
Números racionais podem ser representados:
a) por meio de uma fração;
b) ou por meio de um número decimal.
Quando transformamos uma fração em número decimal, podemos obter:
a) um decimal exato;
b) ou uma dízima periódica.
Dízimas Perióridas podem ser:
a) simples - quando a parte periódica começa logo após a vígula.
b) composta - quando após a vírgula vem uma parte não periódica e posteriormente a parte periódica.
A fração unitária (fração geratriz) 1/17 gera a seguinte dízima periódica simples cujo período é 1 unidade menor que o denominador 17.
| 1 | ||
| ----- | = | 0,0588235294117647 0588235294117647 |
| 17 |
Período: 0 588 235 294 117 647 (16 algarismos)
A frações 1/17 a 16/17 geram dízimas periódicas simples cujos períodos apresentam seus algarismos permutados em relação ao período gerado da fração unitária 1/17: 0 588 235 294 117 647 (16 algarismos).
Observação: conforme se verifica, não há necessidade de se multiplicar o período 0 588 235 294 117 647 por números naturais de 2 a 16 para se obterem números cíclicos.
| Frações de 1/17 a 16/17 | ||
| e números cíclicos | ||
| frações | dízimas periódicas / | |
| números cíclicos | ||
| 1 / 17 | = | 0588235294117647 |
| 2 / 17 | = | 1176470588235294 |
| 3 / 17 | = | 1764705882352941 |
| 4 / 17 | = | 2352941176470588 |
| 5 / 17 | = | 2941176470588235 |
| 6 / 17 | = | 3529411764705882 |
| 7 / 17 | = | 4117647058823529 |
| 8 / 17 | = | 4705882352941176 |
| 9 / 17 | = | 5294117647058823 |
| 10 / 17 | = | 5882352941176470 |
| 11 / 17 | = | 6470588235294117 |
| 12 / 17 | = | 7058823529411764 |
| 13 / 17 | = | 7647058823529411 |
| 14 / 17 | = | 8235294117647058 |
| 15 / 17 | = | 8823529411764705 |
| 16 / 17 | = | 9411764705882352 |
| www.osfantasticosnumerosprimos.com.br | ||
Fração unitária em que o numerador é 1 e o denominador determinado número primo, apresenta uma interessante propriedade numérica que é a de gerar números cíclicos, propriedades estas e outras estudadas pelo Matemático frânces Étienne Midy em 1836, até ser redescoberto em 2004 por Brian Ginsberg. [1]
Martin Gardner, em seu livro Circo Matemático, relata: "que entre os números primos menores que 100 há exatamente nove que geram números cíclicos, a saber: 7, 17, 19, 23, 29, 47, 59, 61 e 97.” [1]
Dizímas periódicas simples cujos períodos possuem quantidade de algarismos pares apresenta uma propriedade muito interessante.
Dividindo-se o período em duas partes e somando-os, o resultado é um número somente com algarismos 9.
Exemplo:
Período: 05882352 94117647 (16 algarismos) da fração 1/17.
| 05882352 | |
| + | 94117647 |
| ------------ | |
| 99999999 |
Propriedade esta descoberta pelo Matemático francês Étienne Midy em 1836. [1]
As dízimas periódicas originadas das frações de 1/17 a 16/17 formam progressão aritmética cuja razão é o período 058 823 529 411 7647 (número cíclico).
| Frações | ||||
| de 1/17 a 16 / 17 | ||||
| e progressão aritimética | ||||
| fração | dízima | razão | ||
| 1 / 17 | = | 0588235294117647 | = | |
| 2 / 17 | = | 1176470588235294 | = | 0588235294117647 |
| 3 / 17 | = | 1764705882352941 | = | '' |
| 4 / 17 | = | 2352941176470588 | = | '' |
| 5 / 17 | = | 2941176470588235 | = | '' |
| 6 / 17 | = | 3529411764705882 | = | ' |
| 7 / 17 | = | 4117647058823529 | = | '' |
| 8 / 17 | = | 4705882352941176 | = | '' |
| 9 / 17 | = | 5294117647058823 | = | '' |
| 10 / 17 | = | 5882352941176470 | = | '' |
| 11 / 17 | = | 6470588235294117 | = | '' |
| 12 / 17 | = | 7058823529411764 | = | '' |
| 13 / 17 | = | 7647058823529411 | = | '' |
| 14 / 17 | = | 8235294117647058 | = | '' |
| 15 / 17 | = | 8823529411764705 | = | '' |
| 16 / 17 | = | 9411764705882352 | = | '' |
| www.osfantasticosnumerosprimos.com.br | ||||
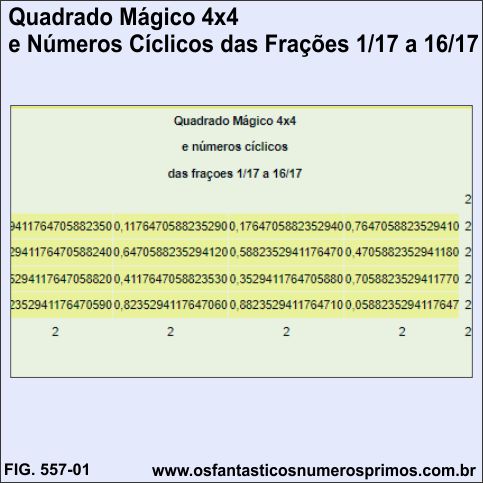
Quadrado Mágico 4x4 e números cíclicos das frações 1/17 a 16/17.
Soma de cada linha: 2
Soma de cada coluna: 2
Soma de cada diagonal: 2
Soma de todos os números: 8
Constante Mágica 2:
| Quadrado Mágico 4x4 | |||||
| e números cíclicos | |||||
| das fraçoes 1/17 a 16/17 | |||||
| 2 | |||||
| 0,9411764705882350 | 0,1176470588235290 | 0,1764705882352940 | 0,7647058823529410 | 2 | |
| 0,2941176470588240 | 0,6470588235294120 | 0,5882352941176470 | 0,4705882352941180 | 2 | |
| 0,5294117647058820 | 0,4117647058823530 | 0,3529411764705880 | 0,7058823529411770 | 2 | |
| 0,2352941176470590 | 0,8235294117647060 | 0,8823529411764710 | 0,0588235294117647 | 2 | |
| 2 | 2 | 2 | 2 | 2 | |
| www.osfantasticosnumerosprimos.com.br | |||||
O número primo 17 menos 1 unidade é igual a 16 e que corresponde a quadrado mágico 4x4, isto é, 4 linhas e 4 colunas (16 células).
Número primo terminado em 1 e subtraído 1 unidade terá como diferença número terminado em 0.
Há números quadrados perfeitos terminado em 0 (zero).
Número primo terminado em 3 e subtraído 1 unidade terá como diferença número terminado em 2.
Não há quadrado perfeito terminado em 2.
Número primo terminado em 9 e subtraído 1 unidade terá como diferença número terminado em 8.
Não há quadrado perfeito terminado em 8.
Portanto, os futuros quadrados mágicos a serem construídos com números cíclicos necessariamente serão originados de números primos terminados em 1 ou 7 e as quantidades de algarismos dos períodos serem exatamente p-1 e cujo número seja quadrado perfeito.
17 - 1 = 16 é quadrado perfeito
(p-1) = 16 (comprovado)
257 - 1 = 256 é quadrado perfeito
(p-1) = 256 (comprovado)
Para construir tal quadrado mágico, precisa verificar as seguintes etapas:
a) se a fração 1/257 gera número cíclico com 256 algarismos. (calculadora / planilha com pelos menos 270 casas decimais);
b) se o número com 256 algarismos separados em duas partes e somados têm resultados algarismos 9;
c) sendo número cíclico, realizar 257 divisões de 1/257 a 256/257;
d) montar quadrado de 256x256 células com algarismos dos números cíclicos (cada número cíclico tem 256 algarismos)
e) montar outro quadrado 16x16 = 256 células, cada célula conterá números de 256 algarismos (números cíclicos).
65.537 - 1 = 65.536 é quadrado perfeito
(p-1) = 65.536 (comprovado)
Para construir tal quadrado mágico, precisa verificar as seguintes etapas:
a) se a fração 1/65.537 gera número cíclico com 65.536 algarismos. (calculadora / planilha com pelos menos 65.700 casas decimais);
b) se o número com 65.536 algarismos separados em duas partes e somados têm resultados algarismos 9;
c) sendo número cíclico, realizar 65.537 divisões de 1/65.537 a 65.536/65.537;
d) montar quadrado de 65.536x65.536 células com algarismos dos números cíclicos (cada número cíclico tem 65.536 algarismos)
e) montar outro quadrado 256x256 = 65.536 células, cada célula conterá números de 65.536 algarismos (números cíclicos).
Veja que:
4^2 = 16 + 1 = 17 é primo
16^2 = 256 + 1 = 257 é primo
256^2 = 65.536 + 1 = 65.537 é primo
Com os algarismos dos números cíclicos gerados das frações 1/17 a 16/17 não foi possível construir um quadrado mágico, mas sim um quadrado semi-magico.
Para mais informações veja:
011-estudos-556-quadrado-semi-magico-16x16-dizimas-periodicas-numeros-ciclicos
e também Matérias Relacionadas abaixo!
Martin Gardner, em seu livro Circo Matemático, relata: "que entre os números primos menores que 100 há exatamente nove que geram números cíclicos, a saber: 7, 17, 19, 23, 29, 47, 59, 61 e 97.” [1]
Analisando os números primos:
a) 7 é Primo de Mersenne, será que 127 e outros Primos de Mersenne que terminam em 7 podem gerar números cíclicos?
b) 17 é um Primo de Fermat, será que 257 e 65.537 que terminam em 7 podem gerar números cíclicos?
c) 7 é 1 unidade maior que o número perfeito 6.
d) 29 é 1 unidade maior que o número perfeito 28.
e) será que 33.550.337 e 137.438.691.329 que são primos e 1 unidade maior que os perfeitos 33.550.336 e 137.438.691.328 respectivamente e outros podem gerar números cíclicos?
Autor:Ricardo Silva - abril/2025
[1] ALVES, Diego Pereira. Dízimas Periódicas: Números Cíclicos e Teorema de Midy / Diego Pereira Alves. – 2022.40 f. Dissertação (mestrado) – Universidade Federal do Ceará, Centro de Ciências, Departamento de Matemática, Programa de Pós-Graduação em Matemática em Rede Nacional, Fortaleza, 2022.
[2] GARDNER, Martin. Circo matemático. Madri: Alianza Editorial, 1979. Disponível em:
http://www.librosmaravillosos.com/
in%20Gardner.pdf.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato