logotipo os fantasticos numeros primos
capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo
Página de estudos de matemática e sequências numéricas

Números Primos e Dízimas Periódicas - 559

Números Primos são números que possuem 2 divisores, o número 1 e ele mesmo.

Produtos de números primos geram números compostos.

O presente estudo demonstra que determinados números primos que são denominadores de frações unitárias geram dízimas períodicas simples cujos períodos são formados por quantidades de algarismos que correspondem a 1/3 de p-1, isto é, número primo menos 1 unidade.

Números Primos e Dízimas Periódicas

Esses períodos divididos em 2 blocos e somados os algarismos correspondentes têm resultados sequência de algarismos 9, estes mesmos períodos concatenados 3 vezes e divididos também em 2 blocos, as somas dos algarismos correspondentes somam 9.

Em seu minicurso: Dízimas periódicas e o teorema de
Étienne Midy - Dízimas periódicas, seus períodos e seus comprimentos, ministrado pelo Professor João Carlos Vieira Sampaio, na XI BIENAL DE MATEMÁTICA 2024, apresenta o seguinte resumo:

"Ao explorar dízimas periódicas surge a pergunta sobre como determinar o comprimento (número de dígitos) do período da dízima periódica sem que conheçamos quais são os dígitos da dízima. Isto é possível com o uso de congruências módulo m, um conceito a ser revisado brevemente no minicurso. Por exemplo, de um teorema de Gauss [5], a dízima periódica de fração geratriz 1/31 terá comprimento 15 porque 1015 ≡ 1 (mod 31), e 15 é o primeiro inteiro positivo l (éle manuscrito) tal que 10 l (ele) ≡ 1 (mod 31). Dentre outras propriedades de dízimas periódicas a serem exploradas neste minicurso, temos o teorema de Étienne Midy [6, 12], que em 1836 demonstrou que, considerando-se por exemplo 1/7 = 0, 142857, temos 142 + 857 = 999, esta soma sendo um número descrito por uma fileira de noves, e que esta propriedade também é válida para todas as frações irredutíveis n/p, em que o denominador p é primo, p ≥ 7, e a dízima periódica correspondente se subdivide em dois blocos de mesmo comprimento. Em 2004 Brian Ginsberg [6] chamou a atenção para o fato de que, considerando-se por exemplo a fração “unitária” 1/7 = 0, 142857, temos 14 + 28 + 57 = 99, ainda um resultado descrito por uma fileira de noves, e que esta propriedade é válida para frações 1/p em que o denominador p é primo e o período da dízima pode ser subdividido em três blocos de comprimentos iguais." [1]

O grifo é nosso.

Como se observa, com brilhante maestria, o Professor João Carlos Vieira Sampaio apresenta propriedades de frações irredutíveis.

Martin Gardner, em seu livro Circo Matemático, relata: "que entre os números primos menores que 100 há exatamente nove que geram números cíclicos, a saber: 7, 17, 19, 23, 29, 47, 59, 61 e 97.” [2]

Analisando os números primos:

a) 7 é Primo de Mersenne, será que 127 e outros Primos de Mersenne que terminam em 7 podem gerar números cíclicos?

b) 17 é um Primo de Fermat, será que 257 e 65.537 que terminam em 7 podem gerar números cíclicos?

c) 7 é 1 unidade maior que o número perfeito 6.

d) 29 é 1 unidade maior que o número perfeito 28.

e) será que 33.550.337 e 137.438.691.329 que são primos e 1 unidade maior que os números perfeitos 33.550.336 e 137.438.691.328 respectivamente e outros podem gerar números cíclicos?

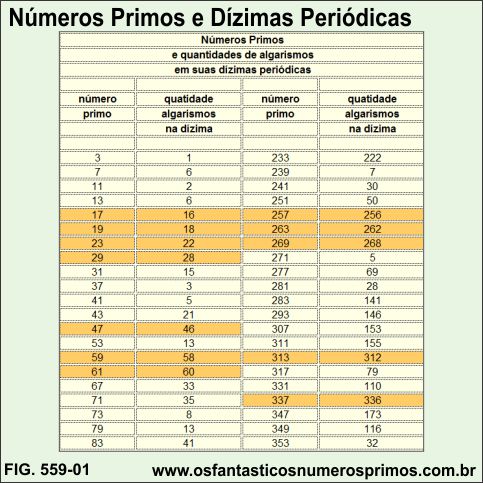
Anteriormente à publicação do livro Circo Matemático foi publicada a seguinte tabela com os menores primos abaixo de 521 com suas respectivas quantidades de algarismos no período de suas dízimas períodicas.

Os números primos destacados em laranja têm quantidades de algarismos nos períodos de suas dízimas (p - 1), isto é, quantidades de algarismos 1 unidade menor que este número primo.

Interessante observar que o número primo 127 (Número Primo de Mersenne), não se encaixa à regra, tem quantidades de 42 algarismos no período de sua dízima periódica, isto é, as quantidades de algarismos não é p-1 ( 127 - 1 = 126) e sim 1/3 de 126.

Números Primos
e quantidades de algarismos
em suas dízimas periódicas
       
número quatidade número quatidade
primo algarismos primo algarismos
  na dízima   na dízima
       
3 1 233 222
7 6 239 7
11 2 241 30
13 6 251 50
17 16 257 256
19 18 263 262
23 22 269 268
29 28 271 5
31 15 277 69
37 3 281 28
41 5 283 141
43 21 293 146
47 46 307 153
53 13 311 155
59 58 313 312
61 60 317 79
67 33 331 110
71 35 337 336
73 8 347 173
79 13 349 116
83 41 353 32
89 44 359 179
97 96 367 366
101 4 373 186
103 34 379 378
107 53 383 382
109 108 389 388
113 112 397 99
127 42 401 200
131 130 409 204
137 8 419 418
139 46 421 140
149 148 431 215
151 75 433 432
157 78 439 219
163 81 443 221
167 166 449 32
173 43 457 152
179 178 461 460
181 180 463 154
191 95 467 233
193 192 479 239
197 98 487 486
199 99 491 490
211 30 499 498
223 222 503 502
227 113 509 208
229 228 521 52

Fonte: adaptado de: DOLISI, Earl E. Periodic Decimal Fractions. A Thesis Presented to the Faculty of the Department of Mathematics Kansas State Teachers College of Emporia, August, 1973. [3]

Número Primo 127 (Número Primo de Mersenne)

O Número Primo de Mersenne é um número especial, pois:

(127 x 128) / 2 = 8128 ( quarto número perfeito ).

O Número Primo de Mersenne 127 é gerado da base 2 elevada ao expoente 7 menos 1 ( 2^7 - 1 = 127 ).

Conforme a tabela acima, as quantidades de algarismos do período da dízima periódica gerada pela fração 1/127 é 42.

Vejamos:

42 corresponde a 1/3 de 126

126 : 3 = 42

127 - 1 = 126

Interessante observar que:

a) efetuando-se cálculos de divisões de 1/127...

Resto da Divisão
       
etapas dividendo divisor resto da quociente
divisões divisão (algarismos da
  dízima
  periódica)
   
1 0
2 0
3 1000 127 111 7
4 111 1110 127 94 8
5 94 940 127 51 7
6 51 510 127 2 4
7 2 2 127 2 0
8 2 200 127 73 1
9 73 730 127 95 5
10 95 950 127 61 7
11 61 610 127 102 4
12 102 1020 127 4 8
13 4 4 127 4 0
14 4 400 127 19 3
15 19 190 127 63 1
16 63 630 127 122 4
17 122 1220 127 77 9
18 77 770 127 8 6
19 8 8 127 8 0
20 8 800 127 38 6
21 38 380 127 126 2
22 126 1260 127 117 9
23 117 1170 127 27 9
24 27 270 127 16 2
25 16 160 127 33 1
26 33 330 127 76 2
27 76 760 127 125 5
28 125 1250 127 107 9
29 107 1070 127 54 8
30 54 540 127 32 4
31 32 320 127 66 2
32 66 660 127 25 5
33 25 250 127 123 1
34 123 1230 127 87 9
35 87 870 127 108 6
36 108 1080 127 64 8
37 64 640 127 5 5
38 5 5 127 5 0
39 5 500 127 119 3
40 119 1190 127 47 9
41 47 470 127 89 3
42 89 890 127 1 7
           
www.osfantasticosnumerosprimos.com.br

b) ...obtem-se os 42 algarismos da dízima períodica do número primo 127, e dividindo-os em 2 blocos de 21 algarismos cada e somando-os, os resultados são números com algarismos 9.

Número Primo 127
e dizíma periódica
       
quantidade quociente   soma
de (algarismos)   dos blocos
algarismos      
  primeiro bloco segundo bloco  
       
1 0 9 9
2 0 9 9
3 7 2 9
4 8 1 9
5 7 2 9
6 4 5 9
7 0 9 9
8 1 8 9
9 5 4 9
10 7 2 9
11 4 5 9
12 8 1 9
13 0 9 9
14 3 6 9
15 1 8 9
16 4 5 9
17 9 0 9
18 6 3 9
19 0 9 9
20 6 3 9
21 2 7 9
       
  segundo bloco    
22 9    
23 9    
24 2    
25 1    
26 2    
27 5    
28 9    
29 8    
30 4    
31 2    
32 5    
33 1    
34 9    
35 6    
36 8    
37 5    
38 0    
39 3    
40 9    
41 3    
42 7    
       
www.osfantasticosnumerosprimos.com.br

c) concatenando os 42 algarismos da dízima períodica do número primo 127 e dividindo-os em 2 blocos de 63 algarismos cada e somando-os, os resultados são números com algarismos 9.

Número Primo 127
e dizíma periódica
 
quantidade quociente   soma
  (algarismos)   dos blocos
       
  primeiro bloco segundo bloco  
       
1 0 9 9
2 0 9 9
3 7 2 9
4 8 1 9
5 7 2 9
6 4 5 9
7 0 9 9
8 1 8 9
9 5 4 9
10 7 2 9
11 4 5 9
12 8 1 9
13 0 9 9
14 3 6 9
15 1 8 9
16 4 5 9
17 9 0 9
18 6 3 9
19 0 9 9
20 6 3 9
21 2 7 9
22 9 0 9
23 9 0 9
24 2 7 9
25 1 8 9
26 2 7 9
27 5 4 9
28 9 0 9
29 8 1 9
30 4 5 9
31 2 7 9
32 5 4 9
33 1 8 9
34 9 0 9
35 6 3 9
36 8 1 9
37 5 4 9
38 0 9 9
39 3 6 9
40 9 0 9
41 3 6 9
42 7 2 9
43 0 9 9
44 0 9 9
45 7 2 9
46 8 1 9
47 7 2 9
48 4 5 9
49 0 9 9
50 1 8 9
51 5 4 9
52 7 2 9
53 4 5 9
54 8 1 9
55 0 9 9
56 3 6 9
57 1 8 9
58 4 5 9
59 9 0 9
60 6 3 9
61 0 9 9
62 6 3 9
63 2 7 9
  segundo bloco    
       
64 9    
65 9    
66 2    
67 1    
68 2    
69 5    
70 9    
71 8    
72 4    
73 2    
74 5    
75 1    
76 9    
77 6    
78 8    
79 5    
80 0    
81 3    
82 9    
83 3    
84 7    
85 0    
86 0    
87 7    
88 8    
89 7    
90 4    
91 0    
92 1    
93 5    
94 7    
95 4    
96 8    
97 0    
98 3    
99 1    
100 4    
101 9    
102 6    
103 0    
104 6    
105 2    
106 9    
107 9    
108 2    
109 1    
110 2    
111 5    
112 9    
113 8    
114 4    
115 2    
116 5    
117 1    
118 9    
119 6    
120 8    
121 5    
122 0    
123 3    
124 9    
125 3    
126 7    
       
www.osfantasticosnumerosprimos.com.br

Números primos e períodos de 1/3 de p-1

A partir da tabela acima, Números Primos e quantidades de algarismos em suas dízimas periódicas, subtraiu-se 1 unidade de cada número primo e dividiu-se por 3, comprovando-se desta forma números primos que realmente têm algarismos nos períodos de suas dízimas que correspondem a 1/3 de p-1.

Os números primos destacados em laranja são os que têm algarismos em seus períodos 1/3 de p-1 e também aparecem na tabela acima.

Observação: as quantidades 1/3 são todos números pares que somados 3 vezes e mais 1 unidade resultam em números primos.

( 34 + 34 + 34 ) + 1 = 103

( 42 + 42 + 42 ) + 1 = 127

( 46 + 46 + 46 ) + 1 = 139

                   
                   
primo quat. primo quat. primo quat. primo quat. primo quat.
  alg.   alg.   alg.   alg.   alg
  per.   per.   per.   per.   per.
  1/3   1/3   1/3   1/3   1/3
                   
                   
3 0,6 83 27,3 191 63,3 307 102 431 143,3
7 2 89 29,3 193 64 311 103,3 433 144
11 3,3 97 32 197 65,3 313 104 439 146
13 4 101 33,3 199 66 317 105,3 443 147,3
17 5,3 103 34 211 70 331 110 449 149,3
19 6 107 35,3 223 74 337 112 457 152
23 7,3 109 36 227 75,3 347 115,3 461 153,3
29 9,3 113 37,3 229 76 349 116 463 154
31 10 127 42 233 77,3 353 117,3 467 155,3
37 12 131 43,3 239 79,3 359 119,3 479 159,3
41 13,3 137 45,3 241 80 367 122 487 162
43 14 139 46 251 83,3 373 124 491 163,3
47 15,3 149 49,3 257 85,3 379 126 499 166
53 17,3 151 50 263 87,3 383 127,3 503 167,3
59 19,3 157 52 269 89,3 389 129,3 509 169,3
61 20 163 54 271 90 397 132 521 173,3
67 22 167 55,3 277 92 401 133,3    
71 23,3 173 57,3 281 93,3 409 136    
73 24 179 59,3 283 94 419 139,3    
79 26 181 60 293 97,3 421 140    

Fonte: adaptado de: DOLISI, Earl E. Periodic Decimal Fractions. A Thesis Presented to the Faculty of the Department of Mathematics Kansas State Teachers College of Emporia, August, 1973. [3]

Os números primos 103, 139, 349, 421, 457 e 463 possuem propriedades idênticas as do número 127 (Número Primo de Mersenne) demonstradas acima.

Número Primo 103

Efetuando divisões da fração unitária 1/103, obtem-se a dízima com 34 algarismos que corresponde a 1/3 de (103 - 1 = 102).

Resto da Divisão
             
etapas   dividendo divisor quociente múltiplos resto
divisões   inteiro de divisão
  (algarismos 103
da dízima)
 
1 0
2 0
3 1000 103 9 927 73
4 73 730 103 7 721 9
5 9 90 103 0 0 90
6 90 900 103 8 824 76
7 76 760 103 7 721 39
8 39 390 103 3 309 81
9 81 810 103 7 721 89
10 89 890 103 8 824 66
11 66 660 103 6 618 42
12 42 420 103 4 412 8
13 8 80 103 0 0 80
14 80 800 103 7 721 79
15 79 790 103 7 721 69
16 69 690 103 6 618 72
17 72 720 103 6 618 102
18 102 1020 103 9 927 93
19 93 930 103 9 927 3
20 3 30 103 0 0 30
21 30 300 103 2 206 94
22 94 940 103 9 927 13
23 13 130 103 1 103 27
24 27 270 103 2 206 64
25 64 640 103 6 618 22
26 22 220 103 2 206 14
27 14 140 103 1 103 37
28 37 370 103 3 309 61
29 61 610 103 5 515 95
30 95 950 103 9 927 23
31 23 230 103 2 206 24
32 24 240 103 2 206 34
33 34 340 103 3 309 31
34 31 310 103 3 309 1
             
www.osfantasticosnumerosprimos.com.br

Dividindo-se a dízima de 34 algarismos em dois blocos de 17 algarismos e somando os algarismos correspondentes, os resultados são números somente com algarimo 9.

Número Primo 103
e dizíma periódica
         
quantidade dízima primeiro segundo soma
algarismos periódica bloco bloco dos blocos
         
1 0 0 9 9
2 0 0 9 9
3 9 9 0 9
4 7 7 2 9
5 0 0 9 9
6 8 8 1 9
7 7 7 2 9
8 3 3 6 9
9 7 7 2 9
10 8 8 1 9
11 6 6 3 9
12 4 4 5 9
13 0 0 9 9
14 7 7 2 9
15 7 7 2 9
16 6 6 3 9
17 6 6 3 9
18 9
19 9
20 0
21 2
22 9
23 1
24 2
25 6
26 2
27 1
28 3
29 5
30 9
31 2
32 2
33 3
34 3      
         
www.osfantasticosnumerosprimos.com.br

Concatenando a dízima de 34 algarismos 3 vezes e a separando em dois blocos de 51 algarismos cada e somando os algarismos correspondentes, os resultados são números somente com algarismo 9.

Número Primo 103
e dizíma periódica
         
quantidade dízima primeiro segundo soma
algarismos concatenada bloco bloco dos blocos
  3 vezes      
         
1 0 0 9 9
2 0 0 9 9
3 9 9 0 9
4 7 7 2 9
5 0 0 9 9
6 8 8 1 9
7 7 7 2 9
8 3 3 6 9
9 7 7 2 9
10 8 8 1 9
11 6 6 3 9
12 4 4 5 9
13 0 0 9 9
14 7 7 2 9
15 7 7 2 9
16 6 6 3 9
17 6 6 3 9
18 9 9 0 9
19 9 9 0 9
20 0 0 9 9
21 2 2 7 9
22 9 9 0 9
23 1 1 8 9
24 2 2 7 9
25 6 6 3 9
26 2 2 7 9
27 1 1 8 9
28 3 3 6 9
29 5 5 4 9
30 9 9 0 9
31 2 2 7 9
32 2 2 7 9
33 3 3 6 9
34 3 3 6 9
35 0 0 9 9
36 0 0 9 9
37 9 9 0 9
38 7 7 2 9
39 0 0 9 9
40 8 8 1 9
41 7 7 2 9
42 3 3 6 9
43 7 7 2 9
44 8 8 1 9
45 6 6 3 9
46 4 4 5 9
47 0 0 9 9
48 7 7 2 9
49 7 7 2 9
50 6 6 3 9
51 6 6 3 9
52 9
53 9
54 0
55 2
56 9
57 1
58 2
59 6
60 2
61 1
62 3
63 5
64 9
65 2
66 2
67 3
68 3
69 0
70 0
71 9
72 7
73 0
74 8
75 7
76 3
77 7
78 8
79 6
80 4
81 0
82 7
83 7
84 6
85 6
86 9
87 9
88 0
89 2
90 9
91 1
92 2
93 6
94 2
95 1
96 3
97 5
98 9
99 2
100 2
101 3
102 3
   
www.osfantasticosnumerosprimos.com.br

A tabela a seguir apresenta as diferenças, bem como, as respectivas frações correspondentes de ( p - 1 ), isto é, da diferença de um número primo subtraído 1 unidade.

As frações 1/1 são as frações correspondentes de números que são efetivamente 1 unidade menor que um número primo.

Números Primos
e frações correspondentes das
quantidades de algarismos
no período de dízimas
         
número quant. fração número quant. fração
primo algaris-   primo algaris-  
mos mos
no período no período
 da dizima   primo da dizima
           
3 1 1 / 3 233 222 1 / 1
7 6 1 / 1 239 7 1 / 34
11 2 1 / 5 241 30 1 / 8
13 6 1 / 2 251 50 1 / 5
17 16 1 / 1 257 256 1 / 1
19 18 1 / 1 263 262 1 / 1
23 22 1 / 1 269 268 1 / 1
29 28 1 / 1 271 5 1 / 54
31 15 1 / 2 277 69 1 / 4
37 3 1/ 13 281 28 1 / 10
41 5 1 / 8 283 141 1 / 2
43 21 1 / 2 293 146 1 / 2
47 46 1 / 1 307 153 1 / 2
53 13 1 / 4 311 155 1 / 2
59 58 1 / 1 313 312 1 / 1
61 60 1 / 1 317 79 1 / 4
67 33 1 / 2 331 110 1 / 3
71 35 1 / 2 337 336 1 / 1
73 8 1 / 9 347 173 1 / 2
79 13 1 / 6 349 116 1 / 3
83 41 1 / 2 353 32 1 / 11
89 44 1 / 2 359 179 1 / 2
97 96 1 / 1 367 366 1 / 1
101 4 1 / 25 373 186 1 / 2
103 34 1 / 3 379 378 1 / 1
107 53 1 / 2 383 382 1 / 1
109 108 1 / 1 389 388 1 / 1
113 112 1 / 1 397 99 1 / 4
127 42 1 / 3 401 200 1 / 2
131 130 1 / 1 409 204 1 / 2
137 8 1 / 17 419 418 1 / 1
139 46 1 / 3 421 140 1 / 3
149 148 1 / 1 431 215 1 / 2
151 75 1 / 2 433 432 1/1
157 78 1 / 2 439 219 1 / 2
163 81 1 / 2 443 221 1 / 2
167 166 1 / 1 449 32 1 / 14
173 43 1 / 4 457 152 1 / 3
179 178 1 / 1 461 460 1 / 1
181 180 1 / 1 463 154 1 / 3
191 95 1 / 2 467 233 1 / 2
193 192 1 / 1 479 239 1 / 2
197 98 1 / 2 487 486 1 / 1
199 99 1 / 2 491 490 1 / 1
211 30 1 / 1 499 498 1 / 1
223 222 1 / 1 503 502 1 / 1
227 113 1 / 2 509 508 1 / 1
229 228 1 / 1 521 52 1 / 10
           
www.osfantasticosnumerosprimos.com.br

Fonte: adaptado de: DOLISI, Earl E. Periodic Decimal Fractions. A Thesis Presented to the Faculty of the Department of Mathematics Kansas State Teachers College of Emporia, August, 1973. [3]

Autor: Ricardo Silva - abril/2025

Fontes Bibliográficas:

[1] GARDNER, Martin. Circo matemático. Madri: Alianza Editorial, 1979. Disponível em:
http://www.librosmaravillosos.com/ circomatematico/pdf/ Circo%20matematico%20-%20Mart
in%20Gardner.pdf. Acesso em: 03 abril. 2025.

[3] DOLISI, Earl E. Periodic Decimal Fractions. A Thesis Presented to the Faculty of the Department of Mathematics Kansas State Teachers College of Emporia, August, 1973.

[1] SAMPAIO, João Carlos Vieira. Dízimas periódicas e o teorema de Étienne Midy. XI BIENAL DE MATEMÁTICA 2024. Disponível em:
https://www.dm.ufscar.br /profs/sampaio/ MC_T7_joao_sampaio- texto- xibienal-corrigido.pdf. Acesso em: 03 abril. 2025.

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-327-numeros-palindromos-e-numeros-racionais-e-irracionais
011-estudos-554-dizimas-periodicas-progressoes-aritmeticas
011-estudos-555-quadrados-magicos-18x18-numeros-ciclicos-fracoes-n-19
011-estudos-556-quadrado-semi-magico-16x16-dizimas-periodicas-numeros-ciclicos
011-estudos-557-quadrado-magico-4x4-numeros-ciclicos-das-fracoes-n-17
011-estudos-558-numeros-ciclicos-e-os-numeros-de-fermat-mersenne-perfeitos
Livro digital (e-book)
Escada de Theon
e Sequências Numéricas
Escada de Theon e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Primos e o
Método Números Atraentes
livro Números Primos e o Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Progressões Aritméticas e Geométricas
livro digital Progressões Aritméticas e Geometricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Tabuada de Pythagoras
e Sequências Numéricas
livro digital Tabuada de Pythagoras e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Estudos de Sequências Numéricas
livro estudos de sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Os Fantásticos Números Primos
livro os fantasticos números primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Ternos Pitagóricos e Sequências Numéricas
livro Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE
o E-book
Triângulo Retângulo

 

livro Triângulo Retângulo

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos
livro descobrindo numeros primos a partir numeros compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas
livro quadrados mágicos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas
livro triangulares e sequências numéricas mágicas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo
livro quadrado mágico triplo
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Perfeitos e Sequências Numéricas
livro Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos
livro multiplicação através da soma de múltiplos
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.

curta fantasticos numeros primos no facebook
anúncio dominó tri-minox anúncio dominó quadriminox
logotipo Ric Desing

Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.

Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).

Desenvolvimento de WebSite.

Contato

ric@osfantasticosnumerosprimos.com.br

fapage dos fantasticos numeros primos
Canal youtube dos fantasticos numeros primos