


A essência da Equação do Segundo Grau é descobrir dois números cuja a soma e produto são dados, isto é, descobrir suas raízes e o método subjacente em descobrir tais números é o Método de Completar Quadrados.
Pesquisas realizadas em tabletes de barro com escritas cuneiformes constataram conhecimento e aplicação de Equações do Segundo Grau pelos povos mesopotâmicos, mas especificamente a civilização da Babilônia.
As equações não eram da forma como temos hoje, mas sim em textos escritos como se fossem "receitas".
Vitor J. KATZ em seu livro, A History of Mathematics an introduction, presume que os procedimentos, isto é, os algorítmos, para a resolução de Equações do Segundo Grau tenham sido idealizados a partir de conceitos geométricos.
A partir de figuras geométricas de quadrados e formando retângulos cujos comprimentos sejam o dobro de seus lados e posteriormente reconfigurando esses retângulos em quadrados novamente, a figura formada se parecerá com uma "cantoneira", isto é, um "quase-quadrado".
Para formar realmente o quadrado, precisa ser acrescentado uma área quadrada faltante.
Somando-se 1 unidade aos "quase-quadrados" obtem-se um quadrado perfeito.
3 + 1 = 4
8 + 1 = 9
15 + 1 = 16
Veja matérias relacionadas:
005-texto-023-equacao-segundo-grau-com-quadrados-retangulos
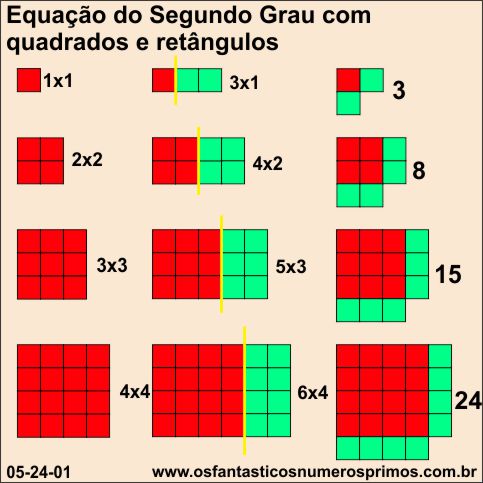
Escolhendo-se dois números consecutivos ímpares ou dois números consecutivos pares, podemos relacioná-los com alturas e larguras de figuras geométricas de retângulos.
Efefuando-se posteriormente a soma e o produto desses números consecutivos obtem-se também o semiperímetro e à área desses retângulos.
Tabulando os dados entre quadrados e retângulos conforme a figura (05-24-01), verifica-se que a medida da altura e largura são as respectivas raízes do semiperímetro e da área de um retângulo referente a um quadrado cujo lado tem a mesma medida da altura desse retângulo, fato este que também pode ser comprovado aplicando o Método de Completar Quadrados na Equação do Segundo Grau.
Interessante observar que excetuando-se as colunas área e quase-quadrados perfeitos, as demais colunas de sequências numéricas da tabela formam Progressões Aritméticas (P.A.s).
As sequências numéricas das colunas área e quase-quadrados têm como diferenças entre seus termos números ímpares.
| Relações numéricas entre | |||||
|---|---|---|---|---|---|
| quadrados e retângulos | |||||
| Quadrado | Retângulo | ||||
| semi- | quase- | ||||
| lado | altura | largura | área | perímetro | quadrados |
| perfeitos | |||||
| produto | soma | ||||
| x | c | b | |||
| 1 | 1 | 3 | 3 | 4 | 3 |
| 2 | 2 | 4 | 8 | 6 | 8 |
| 3 | 3 | 5 | 15 | 8 | 15 |
| 4 | 4 | 6 | 24 | 10 | 24 |
| 5 | 5 | 7 | 35 | 12 | 35 |
| 6 | 6 | 8 | 48 | 14 | 48 |
| 7 | 7 | 9 | 63 | 16 | 63 |
| 8 | 8 | 10 | 80 | 18 | 80 |
| 9 | 9 | 11 | 99 | 20 | 99 |
| 10 | 10 | 12 | 120 | 22 | 120 |
| www.osfantasticosnumerosprimos.com.br | |||||
Com o Método de Completar Quadrados podemos resolver Equações do Segundo Grau.
Escolhendo-se os dados da tabela acima referente ao quadrado de lado "x", por exemplo, formulando Equação do Segundo Grau com as medidas da área e semiperímetro do retângulo obtem-se suas respectivas raízes.
Exemplo:
Quanto mede a altura de um retângulo cuja largura é duas unidades a mais que sua altura, sabendo-se que sua área é 3 unidades quadradas.
x (x+2) = 3
x2 + 2x = 3
Dividi-se o coeficiente 2 do termo "bx" por 2 e eleve ao quadrado (12) e some-o ao primeiro e segundo membros para equilibrar a equação.
x2 + 2x + 12 = 3 + 12
x2 + 2x + 1 = 3 + 1
O primeiro membro torna-se um Trinômio Quadrado Perfeito.
x2 + 2x + 1 = 3 + 1
Fatora-se o primeiro membro, obtendo-se o quadrado da soma (produto notável).
(x + 1)2 = 4
Extrai-se a raiz quadrada dos dois membros.
x + 1 = ± √4
x + 1 = ± 2
x' = + 2 - 1 = 1
x" = - 2 - 1 = - 3
Na utilização da Fórmula Geral (Fórmula de Bháskara), pode-se inicialmente fazer uso do Discriminante da Equação do Segundo Grau representado pela letra grega Delta (Δ) para se saber quantas raízes reais a equação tem.
| - b ± √b 2 - 4 . a .c | ||
| x | = | _____________ |
| 2.a |
| Δ = b2 - 4 . a . c |
Quando Δ > 0 (maior que 0), a equação tem duas raízes reais distintas.
Quando Δ = 0 (igual a 0), a equação tem duas raízes reais iguais.
Quando Δ < 0 (menor que 0), a equação não tem raízes reais.
Aplicando-se o Delta (Δ) com pares de números referente ao semiperímetro e área (coeficentes b e c) de um retângulo da tabela acima, obtem-se o Δ = 4 constante.
| Quadrado | Retângulo | ||||
| semi- | quase- | ||||
| lado | altura | largura | área | perímetro | quadrados |
| perfeitos | |||||
| x | a | c | b | ||
| 1 | 1 | 3 | 3 | 4 | 3 |
x (x+2) = 3
x2 + 2x = 3
Δ = b2 - 4 . a. c
Δ = (-4)2 - 4 . 1 . 3
Δ = 16 - 12
Δ = 16 - 12
Δ = 4
| Quadrado | Retângulo | ||||
| semi- | quase- | ||||
| lado | altura | largura | área | perímetro | quadrados |
| perfeitos | |||||
| x | a | c | b | ||
| 2 | 2 | 4 | 8 | 6 | 8 |
x(x+6) = 8
x2 + 6x = 8
Δ = b2 - 4 . a. c
Δ = (-6)2 - 4 . 1 . 8
Δ = 36 - 32
Δ = 4
| lado | altura | largura | área | perímetro | quadrados |
| perfeitos | |||||
| produto | soma | ||||
| x | |||||
| a | c | b | |||
| 3 | 3 | 5 | 15 | 8 | 15 |
x(x+8) = 15
x2 + 8x = 15
Δ = b2 - 4 . a. c
Δ = (-8)2 - 4 . 1 . 15
Δ = 64 - 60
Δ = 4
| Quadrado | Retângulo | ||||
| semi- | quase- | ||||
| lado | altura | largura | área | perímetro | quadrados |
| perfeitos | |||||
| produto | soma | ||||
| x | a | c | b | ||
| 4 | 4 | 6 | 24 | 10 | 24 |
x(x+10) = 24
x2 + 10x = 24
Δ = b2 - 4 . a. c
Δ = (-10)2 - 4 . 1 . 24
Δ = 100 - 96
Δ = 4
Os números Quase-Quadrados Perfeitos são produtos de ímpares consecutivos ou pares consecutivos que formam uma sequência numérica cuja diferença entre dois termos é número ímpar.
Os números Quase-Quadrados Perfeitos podem ser obtidos por meio da seguinte fórmula:
| n2 - 1 |
Exemplos:
a) 12 - 1 = 0
b) 22 - 1 = 3
c) 32 - 1 = 8
| Números Quase-Quadrados Perfeitos | |
|---|---|
| quase- | Diferença |
| quadrados | números |
| perfeitos | ímpares |
| 3 | |
| 5 | |
| 8 | |
| 7 | |
| 15 | |
| 9 | |
| 24 | |
| 11 | |
| 35 | |
| 13 | |
| 48 | |
| 15 | |
| 63 | |
| 17 | |
| 80 | |
| 19 | |
| 99 | |
| 21 | |
| 120 | |
| www.osfantasticosnumerosprimos.com.br | |
Autor: Ricardo Silva - maio/2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
SAUTOY, Marcus Du. Filme The Story of Maths - The Language of The Universe. The Open University - BBC - XXVIII.
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato