


"A arte do ladrilhamento consiste no preenchimento do plano, por moldes, sem superposição ou buracos. Ela existe desde que o homem começou a usar pedras para cobrir o chão e as paredes de sua casa e continuou com a aplicação de cores, desenhos ou figuras para deixar os ladrilhos mais agradáveis. As mais antigas peças de ladrilhos conhecidas datam de 5000 anos a.C. e foram encontradas no Egito".[4]
Discorrendo sobre O Número de Ouro, o Professor Michel Spira em sua palestra: OBEMEP 2006 - ESTÁGIO DOS PROFESSORES PREMIADOS, publicado posteriormente no YouTube, em 2011, faz uma observação sobre uma das pinturas do artista plástico Piet Moldrian que diz mais ou menos assim:
"Com tantas figuras de quadriláteros justapostas, certamente há de se encontrar seguimentos cujas medidas estão próximas a razão dourada, razão áurea, número de ouro que é 1,618033657... o qual é representado pela letra grega Phi (Ф).

O que o Professor Michel Spira também quiz dizer é que desenhando-se várias figuras geométricas regulares ou não justapostas e superpostas ou vice-versa, certamente, também há de se encontrar seguimentos que contenham o número de ouro.
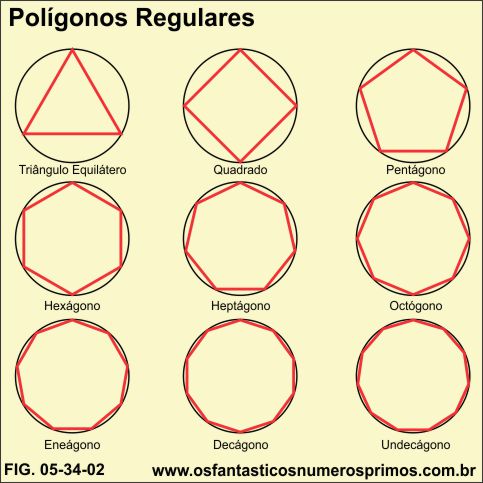
Polígonos regulares são figuras geométricas que têm todos os lados com medidas iguais (congruentes) e também todos os ângulos internos com medidas iguais (congruentes).
Polígono regulares podem ser inscritos e circunscritos numa circunferência.
Diz-se que uma figura é simétrica ou apresenta simetria quando ao dobramos, as partes coincidam.
Exemplos de simetria são os reflexos em espelhos, como também, imagens refletidas nas águas de rios, lagoas, lagos, espelhos d'águas, etc.
Polígonos regulares têm os mesmos números de lados e eixos de simetria.
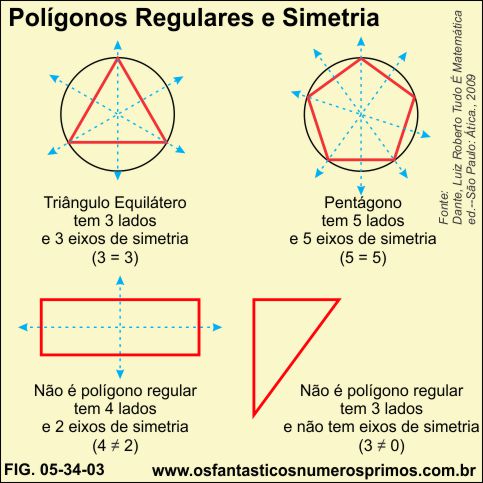
Interessante destacar que:
a) triângulos isóceles, bem como, triângulos equiláteros apresentam simetria, diferentemente de triângulos retângulos escalenos;
b) triângulos retângulos escalenos tem seus 3 lados medidas uma diferente da outra, não apresentam eixos de simetria, é uma figura geométrica irregular, mas subjacente a sua forma está o grande Teorema de Pitágoras, onde: "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" e com o qual são possíveis de realizarem os mais variados cálculos e que são utilizados nos vários ramos das ciências, tais como: astronomia, geometria, engenharia, trigonometria, etc.
Revestimento de paredes, pisos ou fachadas em muitas construções, como casas, escritórios, empresas, edificíos, etc. se utilizam da técnica do ladrilhamento que consiste em assentar azulejos, lajotas, pastilhas, etc., justapostamente, isto é, uma ao lado da outra, e em sua maioria estes azulejos, lajotas, etc., são em formatos quadrados ou retangulares, pois são "mais fáceis" suas colocações pelo profissionais Azulejistas.
Em construções "antigas" ainda é possível de se ver ladrilhamento com azulejos em formatos hexagonais.
A base do ladrilhamento são figuras geométricas planas cujos contornos são polígonos.
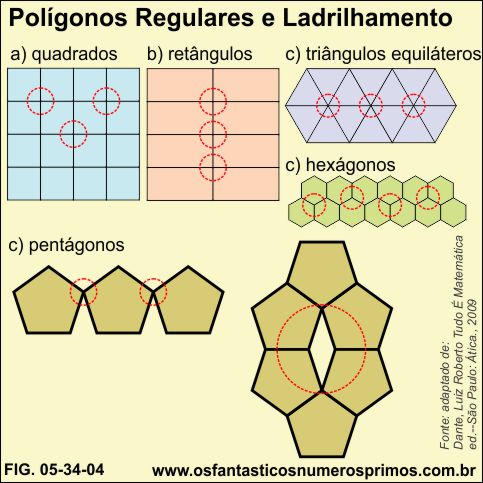
Figuras geométricas planas, como quadrados, retângulos, triângulos equiláteros hexágonos regulares são "próprias" para ladrilhamento, pois suas junções formam ângulos de 360 graus não deixando espaços vazios entre elas.
Outro fato é que estas figuras geométricas formando ladrilhamentos formam eixos de simetrias.
Matemáticos e especialistas denominam de Ladrilhamento Periódico, pois se repetem constantamente em toda superfície.
Diferentemente, pentágonos regulares não são próprios para ladrilhamento, pois deixam espaços em suas junções, veja detalhe c), na ilustração abaixo.
Desde a década 60, matemáticos achavam que era impossível a partir de uma figura irregular criar ladrilhamento aperiódico e assimétrico que pudessem cobrir toda uma superfície.
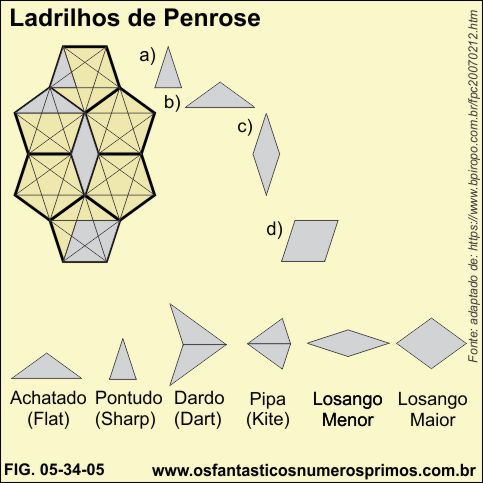
Sir Roger Penrose, (1931-) matemático britânico, físico, filósofo, Ganhador do Prêmio Nobel de Física [1] e também especialista em matemática recreacional [2], em 1974, demonstrou os "Ladrinhos de Penrose", "Mosaico de Penrose", utilizando primeiramente 6 formas e poteriormente reduzindo a apenas duas.
Roger Penrose decompôs um pentágono, extraindo as figuras a, b, d e d e depois a partir delas, criou outras, nomeando-as de: Achatado, Pontudo, Dardo, Pipa (papagaio, quadrado, pandorga); os losangos maior e menor não receberam nomes especiais.
Todas as figuras geradas da decomposição do pentágono tem algo em comum, todas são formadas a partir das combinações de Triângulos de Ouro, também denominados de Triângulos Sublimes, de Triângulos Dourados.
Exemplo de Ladrilho de Penrose contruído exclusivamente com ladrilhos "losango pequeno" e "losango grande" e formando uma imagem aperiódica.
"Há uma relação importante entre os quasicristais e os ladrilhos de Penrose que Roger Penrose já havia encontrado antes da descoberta dos quasicristais: se você cortar um quasicristal corretamente, a superfície de corte mostrará exatamente o padrão dos ladrilhos de Penrose".[5]

O pentágono possui interessantes propriedades geométricas e numéricas, eis algumas delas:
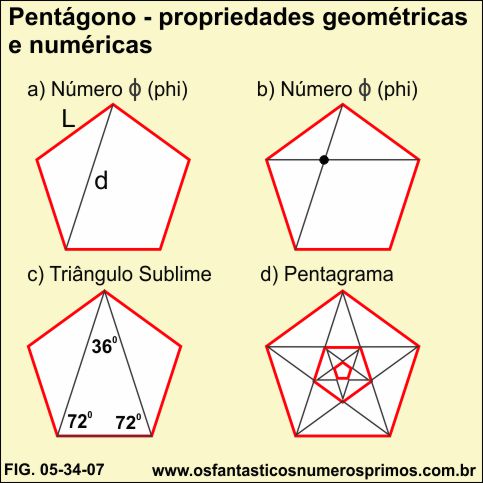
a) a razão entre a medida da diagonal com seu lado tem como resultado o número Φ (phi), isto é, o Número de Ouro;
b) a intersecção de duas diagonais, divide a diagonal em média e extrema razão, conhecida também Secção Áurea cujo resultado é o número Φ (phi), isto é o Número de Ouro;
c) partindo-se de um dos vértices e traçando-se duas diagonais até os ângulos de lados opostos, obtem-se o Triângulo Sublime, triângulo este que apresenta também propriedades relacionadas ao número Φ (phi);
d) traçando-se todas as diagonais do pentágono, obtem-se uma estrela de cinco pontas, denominada de pentagrama cujo em seu interior forma-se um outro pentágono em sentido oposto. Continuando esse processo, mais e mais pentagramas e pentágonos são obtidos infinitamente.
"Recentemente (mais especificamente em fevereiro de 2007) o físico Peter Lu, da Universidade de Cambridge, EUA, publicou na respeitabilíssima revista Science (edição 315, página 1106) um artigo onde relata que encontrou em visita ao Uzbequistão arabescos traçados há de mais de quinhentos anos exibindo rigorosamente os mesmos padrões dos ladrilhos de Penrose?"[2]
Arabesco denominado "girih" que ornamenta o Mausoléu de Seljuk Mama Hatun em Tercan, Turquia, erigido no ano de 1200, semelhante a Ladrilhos de Penrose.

Ornamentação de um dos arcos do alojamento do Sultão da Mesquita Verde da cidade de Bursa, na Turquia, datado de 1424, semelhante a Ladrilhos de Penrose.

Arcada do templo de Darb-i Imam em Isfahan, Irã, construído no ano de 1453, semelhante a Ladrilhos de Penrose.

Técnico de Impressão aposentado, o Sr. David Smith, residente do norte da Inglaterra, vem desde 2016 estudando e tentando criar uma figura irregular para construir ladrilhamento aperiódico.
Eis que em 2022, concretiza a sua criação, com uma figura geométrica de 13 lados, a aqual nomeou de "O Chapéu".
Segundo Rafe Mazzeo, professor do departamento de matemática da Universidade de Stanford, que não participou do estudo, argumentou que: “Os ladrilhos têm muitas aplicações em física, química e além, por exemplo, no estudo de cristais. A descoberta de ladrilhos aperiódicos, já há muitos anos, criou um rebuliço, uma vez que a sua existência era tão inesperada”. [3]

Diferentemente do Matemático Roger Penrose, o Sr. David Smith não patenteou a sua criação e sim a dispolibilizou ao público, de forma que possa ser utilizada nos mais diversos produtos, como também em artes plásticas, arquitetura, etc.
"Um quase-cristal ou quasicristal é um sólido com um espectro de difração essencialmente discreto, como os cristais clássicos, mas com uma estrutura não periódica." [5]
"Em uma manhã de abril de 1982, o químico israelense
Daniel Shechtman estava estudando uma liga de
alumínio e manganês utilizando microscopia
eletrônica. A foto obtida mostrava um padrão de
difração que apresentava círculos concêntricos feitos
de 10 pontos brilhantes a mesma distância. Isso
significava um padrão de simetria de ordem 10. Ele
mesmo não acreditou no que viu porque os resultados
contrariavam a lógica científica vigente. Pensou que
havia ocorrido algum problema com o experimento ou
com a amostra. Assim, tentou buscar explicações e ainda realizou outros testes."[6]

Detalhe a)
Padrão de difração obtido por Daniel Shechtman.
Detalhe b)
Sobre o padrão de difração, estão assinalados os círculos concêntricos contendo 10 pontos cada um e figuras com simetria de ordem 5. A razão entre os raios dos círculos adjacentes é de aproximadamente 1,6 (Número de Ouro).
Ladrilhamento somente com a figura geométrica do pentágono regular, impossível de se concretizar, mas com partes de sua decomposição e formando outras figuras geométricas são possíveis de se criarem ladrilhamentos com estreitas relações com os chamados quase-cristais, relações estas que envolvem diretamente, também, o magnífico número de ouro.
Autor: Ricardo Silva - julho/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1]https://en.wikipedia.org/
[2]https://www.bpiropo.com.br/
[3]https://www.cnnbrasil.com.br/lifestyle/
[4]http://clubes.obmep.org.br/
[5]https://pt.wikipedia.org/wiki/
[6]https://drive.google.com/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato