


Em dezembro de 2.018, foi anunciado o 51o Número de Mersenne, 2 82.589.933 -1 , com 24.862.048 de algarismos, este novo número também é conhecido como M 82.589.933 (M de Mersenne).

Acontecimento este analisado a luz das Ciências, observa-se a aplicação de conhecimentos no desenvolvimento de novos processos e tecnologias para tal feito com a utilização da Matemática, porque sem o uso de computadores seria uma tarefa difícílima para o cérebro humano fazer cálculos e chegar a um resultado cujo número possui 24 milhões de algarismos.
Este número foi calculado por meio do Projeto GIMPS (Great Internet Mersenne Prime Search) que faz uso de um software matemático que é compartilhado na Internet utilizando processadores (CPUs) de milhares de computadores.
Nos estudos do antigos gregos, eles observaram que determinados números quando dividos por 2, deixavam resto 1 e que determinados números possuem somente dois divisores o número 1 e ele próprio.
Estes números são os números primos que fazem parte de uma sequência numérica que vem desafiando ao longo do tempo as mentes matemáticas, bem como entusiastas matemáticos na tentativa se descobrir uma fórmula que consiga gerá-los sequencialmente.
Com um caderno universitário (largura 20cm x altura 27,5cm) com 100 folhas, cada página 33 linhas, cada folha 66 linhas, total de linhas 100 x 66 = 6.600 linhas é possível então escrever 6.600 números, istó é, números de 1 a 6.600.
Pense, comigo, prezado Leitor, de 1 a 10.000 há 1.229 números primos, qual o tempo que levaríamos para elaborar uma tabela/lista com números primos sabendo-se que devemos fazer a Decomposição em Fatores Primos para se saber qual é ou não um número primo?
Qual método ou algoritmo que você utilizaria?
Eratóstenes de Cirene (Cirene, 276 a.C. - Alexandria, 194 a.C.) foi um matemático, gramático, poeta, geógrafo, bibliotecário e astrônomo da Grécia Antiga, foi uma dessas mentes matemáticas, criou um dispositivo numérico, que leva o seu nome Crivo de Eratóstenes, com o qual é possível descobrir números primos.
Querendo-se saber, por exemplo, quantos e quais são os números primos entre os primeiros 100 números naturais, procedemos da seguinte forma:
a) escreve-se números de 1 a 100;
b) risca-se todos os números pares, exceto o número 2;
c) risca-se todos os os múltiplos de 3, exceto o 3;
d) risca-se todos os os múltiplos de 5, exceto o 5;
e) risca-se todos os os múltiplos de 7, exceto o 7;
f) risca-se todos os os múltiplos de 11, exceto o 11;
Os números que não foram riscados são números primos.
Veja materias relacionadas:
011-estudos-028-crivo-eratostenes-sintetico
John Napier (1550-1617), matemático, físico, astrônomo e teólogo escocês. Também era conhecido pelo nome, em latim, de Ioannes Neper.
No início do século XVII, inventou um dispositivo chamado Ossos de Napier que são tabelas de multiplicação gravadas em bastão, permitindo multiplicar e dividir de forma automática, o que evitava a memorização da tabuada.
Em 1614 publicou Mirifici logarithimorum canonis constructio a primeira tábua de logaritmos que consiste em transformar operação de multiplicação em soma e operação de divisão em subtração.

Fonte: Capa do Livro Mirifici logarithimorum canonis constructio de John Napier - https://books.google.fr/
Henry Briggs (1561-1630), matemático, professor da Universidade de Oxford.
Entrou em com contato John Napier e sugeriu-lhe a utilização da base 10 na produção de logaritmos, convecionando-se as seguintes notações: log10 1=0 e log10 10=1.
1617 - publicou Logarithmorum Chillias a primeira tábua de logaritmos de base 10 com 1.000 termos.
1624 - Obra: Aritmetica Logaritmica de 1 a 20.000 e de 90.000 a 100.000 termos.
Adrian Vlacq complementa a Aritmetica Logaritmica dos 20.000 a 90.000 termos.
Na obra Trigonometria Britannica publica logaritmos de 1 a 100.000
Leonhard Paul Euler (1707-1783), matemático e físico suíço de língua alemã.
Produziu tabela com 100.000 número primos.
Johann Heinrich Lambert (1728-1777), matemático suíço radicado na Prússia.
Em 1770, publicou uma coleção de tabelas contendo em particular uma tabela que fornece o menor fator de todos os números inteiros até 102.000 e não divisível por 2, 3 ou 5.
Anton Felkel (1740-1800?), matemático austríaco.
Elaborou tabela de números primos no intervalo entre 1 e mais de 2.000.000.
Publicou em 1776 uma tabela contendo os fatores primos dos números de 1 a 144.000 para os quais não é possível a divisão inteira por 2, por 3 ou por 5.
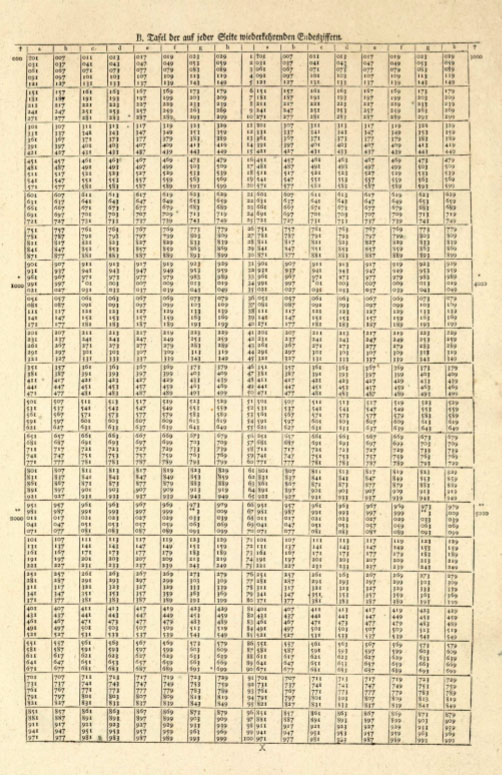
Fonte: Detalhe da Tabela de Primos de Anton Felkel de 1 a 20.353.
(source: GöttingerDigitalisierungszentrum)
Ladislaus Chernac (1742-1816), cientista húngaro que se mudou para Deventer, na Holanda.
Autor da primeira tabela publicada, apresentando decomposições em fatores primários de até um milhão.
Em 1811, publicou em Deventer seu Cribrum arithrneticum, que fornece todos os divisores principais de todos os números não divisíveis por 2, 3 ou 5 até 1.020.000.
Adrien-Marie Legendre (1752-1833), matemático francês.
Em 1798 anuncia a descoberta de uma conexão entre números primos e logaritmos e que posteriormente a publica em sua obra Théorie des nombres (1830).
Neste interím, tenta reivindicar a descoberta para si, não levando em consideração os estudos de Gauss que aos 15 anos também descorbrira relações entre números primos e logaritmos.
Johann Karl Burckhardt (1773-1825), astrônomo e matemático nascido na Alemanha.
Entre 1814 e 1817, Burckhardt publicou em Paris suas Tables des diviseurs, fornecendo o menor divisor de cada número não divisível por 2, 3 ou 5 até 3.036.000.
August Leopold Crelle (1780-1855), matemático alemão que fundou uma importante revista matemática.
Publicado em 1821, Rechentafeln de Crelle (tabelas de computação) foi a primeira tabela amplamente distribuída que oferece produtos de até 1000 × 1000.
Jakob Philipp Kulik (1793-1863),matemático austríaco
Entre 1825 e 1863 (18 anos), Kulik produziu uma tabela fatorial de números até 100.330.200 (exceto números divisíveis por 2, 3 ou 5).
Essas tabelas preenchem oito volumes, totalizando 4.212 páginas, e são mantidas nos arquivos da Academia de Ciências de Viena. O volume II do conjunto de 8 volumes foi perdido.
Johann Carl Friedrich Gauss (1777-1855), matemático, astrônomo e físico alemão.
Ao 15 anos, ganha de presente um livro sobre logaritmos cuja contra-capa havia um tabela de números primos.
A originalidade de Gauss nos estudos de números primos é que ele passou verificar qual era a quantidade de números primos entre intervalos de potências de base 10, detectando um padrão numérico, a quantidade média de números primos em cada intervalo aumenta a uma taxa de 2,3.
Aos 70 anos, Gauss, produzira tabela com 3.000.000 de números primos.
A seguinte tabela apresenta parte dos estudos de Gaus em relação a distribuição de números primos em relação às potencia de 10.
| n | números de primos | quantidade média |
|---|---|---|
| 10 | 4 | 2,5 |
| 100 | 25 | 4,0 |
| 1.000 | 168 | 6,0 |
| 10.000 | 1.229 | 8,1 |
| 1.000.000 | 9.952 | 10,4 |
Fonte: Tabela adaptada de: A música dos números primos, Sautou, Marcus Du.
Derrick Norman Lehmer (1867-1938), matemático estadunidense. Foi especialista em teoria dos números,
Em 1909, Elaborou tabela de números primos de 1 a 10.017.000 que foi publicada pela Carnegie Institution de Washington.
Paí de Derrick Henry "Dick" Lehmer que refinou o algoritmo desenvolvido em 1891 por François Édouard Anatole Lucas - matemático e criador do jogo matemático Torre de Hanoi que detecta se um número de Mersene é ou não é primo.
Autor: Ricardo Silva - junho /2020
SAUTOY, Marcus Du, 1965. A música dos números primos: uma história de um problema não resolvido na matemática / Marcus du Sautoy, Diego Alfaro. - Rio de Janeiro: Jorge Zahar Ed., 2007
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
https://www.mersenne.org/primes/
https://pt.wikipedia.org/
https://pt.wikipedia.org/wiki/
https://pt.wikipedia.org/wiki/
https://pt.wikipedia.org/wiki/
https://en.wikipedia.org/wiki/
https://locomat.loria.fr/felkel1776/
https://pt.wikipedia.org/wiki/
https://books
https://en.wikipedia.org/wiki/
https://mathshistory.st-andrews.ac.uk/Biographies/Crelle/
https://en.wikipedia.org/wiki/
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato