Números semiprimos são números que são produtos de dois números primos.
Os números semiprimos podem ser produtos de um número primo multiplicado por ele mesmo que são os casos de números quadrados perfeitos:
2 x 2 = 4;
3 x 3 = 9;
5 x 5 = 25
ou produtos de dois números primos distintos que são os casos de números compostos que não são quadrados perfeitos e também não são potências de números primos ou de outros números compostos:
2 x 3 = 6;
2 x 5 = 10;
2 x 7 = 14;
3 x 5 = 15;
3 x 7 = 21.
Estudos publicados no livro digital Quadrados Mágicos e Sequências Numéricas, bem como, aqui WebSite Os Fantásticos Números Primos comprovam que potências originadas de números que são produtos de dois números primos distintos (semiprimos) possuem divisores em quantidades de números quadrados perfeitos com os quais são possíveis de se construirem quadrados mágicos multimágicos múltiplicativos sequenciais.
Veja abaixo, matérias relacionadas.
Números triangulares, também denominados de números figurados, são números que podem ser obtidos por meio de arranjos de pontos formando figuras geométricas de triângulos.
Os números triangulares também podem ser obtidos através:
1) da soma de números naturais consecutivos:
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
2) de número retangular (produtos de números consecutivos) dividido por 2:
a)
1 x 2 = 2
2 : 2 = 1
b)
2 x 3 = 6
6 : 2 = 3
b)
3 x 4 = 12
12 : 2 = 6
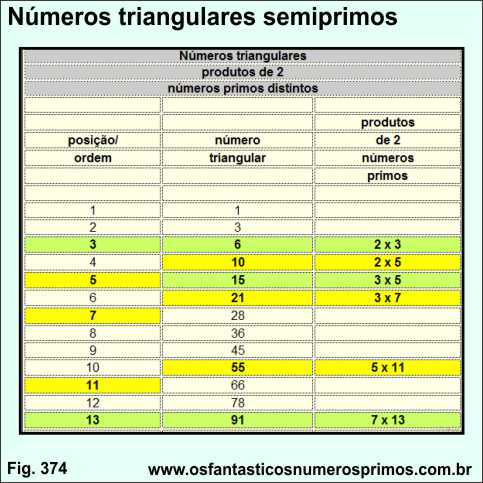
Tabela com os 100 primeiros números triangulares e detalhes de números triangulares que são produtos de 2 números primos distintos.
Observação importante:
a) nas multiplicações de 2 números primos distintos, a partir da multiplicação 5 x 11, os fatores vão aumentando gradativamente: (5 x 11), (7 x 13), (11 x 23), (19 x 37)..., isto é, os números primos surge sequencialmente;
b) os primeiros fatores de cada multiplicação são quase a metade do segundo fator.
2 x 3
2 é um pouco a mais que a metade de 3.
2 x 5
2 é um pouco menos que a metade de 5.
3 x 5
3 é um pouco a mais que a metade de 5.
3 x 7
3 é um pouco menos que a metade de 7.
| Números triangulares | ||
|---|---|---|
| produtos de 2 | ||
| números primos distintos | ||
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 1 | 1 | |
| 2 | 3 | |
| 3 | 6 | 2 x 3 |
| 4 | 10 | 2 x 5 |
| 5 | 15 | 3 x 5 |
| 6 | 21 | 3 x 7 |
| 7 | 28 | |
| 8 | 36 | |
| 9 | 45 | |
| 10 | 55 | 5 x 11 |
| 11 | 66 | |
| 12 | 78 | |
| 13 | 91 | 7 x 13 |
| 14 | 105 | |
| 15 | 120 | |
| 16 | 136 | |
| 17 | 153 | |
| 18 | 171 | |
| 19 | 190 | |
| 20 | 210 | |
| 21 | 231 | |
| 22 | 253 | 11 x 23 |
| 23 | 276 | |
| 24 | 300 | |
| 25 | 325 | |
| 26 | 351 | |
| 27 | 378 | |
| 28 | 406 | |
| 29 | 435 | |
| 30 | 465 | |
| 31 | 496 | |
| 32 | 528 | |
| 33 | 561 | |
| 34 | 595 | |
| 35 | 630 | |
| 36 | 666 | |
| 37 | 703 | 19 x 37 |
| 38 | 741 | |
| 39 | 780 | |
| 40 | 820 | |
| 41 | 861 | |
| 42 | 903 | |
| 43 | 946 | |
| 44 | 990 | |
| 45 | 1035 | |
| 46 | 1081 | 23 x 47 |
| 47 | 1128 | |
| 48 | 1176 | |
| 49 | 1225 | |
| 50 | 1275 | |
| 51 | 1326 | |
| 52 | 1378 | |
| 53 | 1431 | |
| 54 | 1485 | |
| 55 | 1540 | |
| 56 | 1596 | |
| 57 | 1653 | |
| 58 | 1711 | 29 x 59 |
| 59 | 1770 | |
| 60 | 1830 | |
| 61 | 1891 | 31 x 61 |
| 62 | 1953 | |
| 63 | 2016 | |
| 64 | 2080 | |
| 65 | 2145 | |
| 66 | 2211 | |
| 67 | 2278 | |
| 68 | 2346 | |
| 69 | 2415 | |
| 70 | 2485 | |
| 71 | 2556 | |
| 72 | 2628 | |
| 73 | 2701 | 37 x 73 |
| 74 | 2775 | |
| 75 | 2850 | |
| 76 | 2926 | |
| 77 | 3003 | |
| 78 | 3081 | |
| 79 | 3160 | |
| 80 | 3240 | |
| 81 | 3321 | |
| 82 | 3403 | 41 x 83 |
| 83 | 3486 | |
| 84 | 3570 | |
| 85 | 3655 | |
| 86 | 3741 | |
| 87 | 3828 | |
| 88 | 3916 | |
| 89 | 4005 | |
| 90 | 4095 | |
| 91 | 4186 | |
| 92 | 4278 | |
| 93 | 4371 | |
| 94 | 4465 | |
| 95 | 4560 | |
| 96 | 4656 | |
| 97 | 4753 | |
| 98 | 4851 | |
| 99 | 4950 | |
| 100 | 5050 | |
| www.osfantasticosnumerosprimos.com.br | ||
Número triangular cuja ordem / posição é ímpar, o triangular é múltiplo e divisível por esse mesmo número ímpar.
| Números Triangulares | ||
|---|---|---|
| de posições / ordem | ||
| ímpares | ||
| ordem / | Triangular | múltiplo e |
| posição | divisível | |
| 1 | 1 | sim |
| 2 | 3 | |
| 3 | 6 | sim |
| 4 | 10 | |
| 5 | 15 | sim |
| 6 | 21 | |
| 7 | 28 | sim |
Determinados números triangulares cujas ordem / posições são pares, são múltiplos e divisíveis pelas ordem / posições em diagonais.
| Números Triangulares | ||
|---|---|---|
| e divisão em diagonal | ||
| ordem / | Triangular | múltiplo e |
| posição | divisível | |
| 1 | 1 | |
| 2 | 3 | sim |
| 3 | 6 | |
| 4 | 10 | sim |
| 5 | 15 | |
| 6 | 21 | sim |
| 7 | 28 | |
Determinados números triangulares semiprimos apresentam regularidades numéricas em relação às suas ordens / posições com que aparecem na própria sequência dos números triangulares.
Números triangulares cujas ordens / posições são ímpares, o número triangular é divisível por esse número ímpar.
Número triangular cuja ordem / posição é ímpar, isto é, um número primo e dividido por esse primo e tiver como quociente também um número primo, então esse triangular é um triangular semiprimo.
Número triangular cuja ordem / posição é par, dividido em diagonal por um número ímpar, isto é, um número primo, tiver como quociente um número primo, então esse triangular é um triangular semiprimo.
O número triangular 6 é divisível por sua ordem / posição 3.
O número 6 divide 3 em linha reta (célula verde).
3 é um número primo.
6 : 3 = 2
O quociente 2 é um número primo e é metade da ordem / posição 4.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 2 | ||
| 3 | 6 | 2 x 3 |
| 4 |
O número triangular 15 é divisível por sua ordem / posição 5.
O número 15 divide 5 em linha reta (célula verde).
5 é um número primo.
15 : 5 = 3
O quociente 3 é um número primo e é metade da ordem / posição 6.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 4 | ||
| 5 | 15 | 3 x 5 |
| 6 |
O número triangular 91 é divisível por sua ordem / posição 13.
O número 91 divide 13 em linha reta (célula verde).
13 é um número primo.
91 : 13 = 7
O quociente 7 é um número primo e é metade da ordem / posição 14.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 12 | ||
| 13 | 91 | 7 x 13 |
| 14 |
O número triangular 10 é divisível por sua ordem / posição 5.
O número 10 divide 5 em diagonal (célula amarela).
5 é um número primo.
10 : 5 = 2
O quociente 2 é um número primo e é metade da ordem / posição 4.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 4 | 10 | 2 x 5 |
| 5 |
O número triangular 21 é divisível por sua ordem / posição 7.
O número 21 divide 7 em diagonal (célula amarela).
7 é um número primo.
21 : 7 = 3
O quociente 3 é um número primo e é metade da ordem / posição 6.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 6 | 21 | 3 x 7 |
| 7 |
O número triangular 55 é divisível por sua ordem / posição 11.
O número 55 divide 11 em diagonal (célula amarela).
11 é um número primo.
55 : 11 = 5
O quociente 5 é um número primo e é metade da ordem / posição 10.
| produtos | ||
| ordem / | número | de 2 |
| posição | triangular | números |
| primos | ||
| 10 | 55 | 5 x 11 |
| 11 |
Observação muito importante: assim como o triangular 153 cuja ordem / posição é um número primo, há muitos outros números triangulares que não são triangulares semiprimos, vejamos:
O número triangular 153 é divisível por sua ordem / posição 17.
O número 153 divide 17 em linha reta.
17 é um número primo.
153 : 17 = 9
O quociente 9 não é um número primo é divisível por 3.
A soma dos algarismos do número 153 é 1 + 5 + 3 = 9.
153 é um número divisível por 3.
| produtos | ||
| ordem / | número | de 3 |
| posição | triangular | números |
| primos | ||
| 16 | 136 | |
| 17 | 153 | 3 x 3 x 17 |
| 18 | 171 |
O número triangular 435 é divisível por sua ordem / posição 29.
O número 435 divide 29 em linha reta.
29 é um número primo.
435 : 29 = 15
O quociente 15 não é um número primo é divisível por 3 e por 5.
A soma dos algarismos do número 435 é 4 + 3 + 5 = 12.
12 é um número divisível por 3.
| produtos | ||
| ordem / | número | de 3 |
| posição | triangular | números |
| primos | ||
| 28 | ||
| 29 | 435 | 3 x 5 x 29 |
| 30 |
Autor: Ricardo Silva - abril/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Mais informações, acesse:
Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
