


Todo triângulo retângulo inscrito numa semicircunferência é um triângulo retângulo.
Triângulo retângulo de 30, 60 e 90 graus, triângulo equilátero ou triângulo retângulo isóceles de 90, 45 e 45 graus podem ser inscritos numa semicircunferência, bem como numa circunferência de forma "automática" pois possuem ângulos notáveis.
Veja materias relacionadas abaixo, para mais informações.
Até então, para se inscrever um Triângulo Retângulo Pitagórico 3-4-5 numa semicircunferência, o WebSite Os Fantásticos Números Primos demonstrou um novo método geométrico por meio de circunferências concêntricas.
Mesmo utilizando o Método de Circunferências Concêntricas, necessariamente deve-se dividir um seguimento em partes iguais correspondente à hipotenusa do Triângulo Retângulo Pitagórico.
No Método de Circunferências Concêntricas está implícito a Vesica Piscis e a Mandorla.
Veja materias relacionadas abaixo, para mais informações.
Vesica Piscis é uma construção geométrica com duas circunferências em que o centro de uma está sobre a circunferência da outra.
A Mandorla é a intersecção de dois arcos de circunferências.
Neste estudo são demonstrados novos métodos de construções do Triângulo Retângulo Pitagórico 3-4-5 a partir da figuras geométricas da Vesica Piscis e da Mandorla.
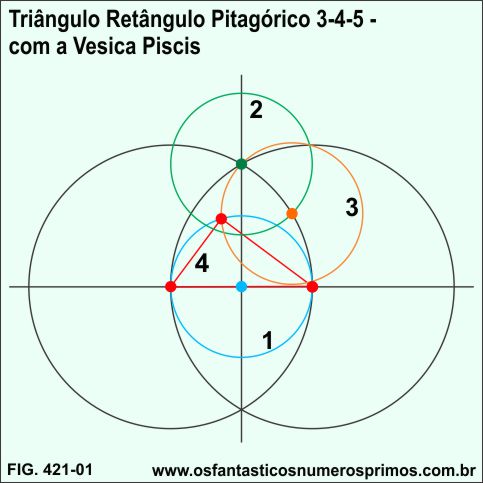
A partir da Vesica Piscis e duas retas perpendiculares:
1) centro nas retas perpendiculares, constrói-se a circunferência (cor azul) com diâmetro da metade do diâmetro da Vesica Piscis;
2) centro na intersecção da Vesica Piscis com a reta vertical, traça uma circunferência (cor verde) de mesmo diâmetro da (cor azul);
3) centro na intersecção da circunferência (cor verde) com a circunferência da Vesica Piscis, traça-se a circunferência (cor laranja) de mesmo diâmetro da (cor azul);
4) unindo-se os pontos de intersecções (cor vermelho), forma-se o Triângulo Retângulo Pitagórico 3-4-5 de ângulos agudos de 37 e 53 graus.
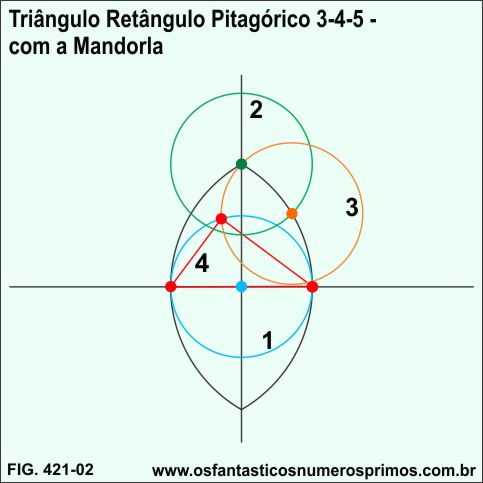
A partir da Mandorla e duas retas perpendiculares:
1) centro nas retas perpendiculares, constrói-se a circunferência (cor azul) tangenciando a Mandorla;
2) centro na intersecção da Mandorla com a reta vertical, traça uma circunferência (cor verde) de mesmo diâmetro da circunferência (cor azul);
3) centro na intersecção da circunferência (cor verde) com a Mandorla, traça-se a circunferência (cor laranja) de mesmo diâmetro da circunferência (cor azul);
4) unindo-se os pontos de intersecções (cor vermelho), forma-se o Triângulo Retângulo Pitagórico 3-4-5 de ângulos agudos de 37 e 53 graus.
Observação importante: com esses novos métodos de construção de Triângulo Retângulo Pitagórico 3-4-5 a partir da Vesica Piscis e da Mandorla, podem ser construídos quaisquer outros Triângulos Retângulos Pitagóricos proporcionais a 3-4-5, como também, triângulos retângulos de lados de números inteiros, simplesmente determinado a medida do raio da circunferência da Vesica Piscis e da Mandorla em número inteiro.
Autor: Ricardo Silva - janeiro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato