


Triângulos Retângulos Pitagóricos são triângulos retângulos cujos lados são formados por sequências de 3 números inteiros e apresentam relação com o Teorema de Pitágoras, que diz que:
"O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" ou "A soma dos quadrados dos catetos é igual a hipotenusa".
| a² = b² + c² |
Há diversos métodos de se gerarem ternos pitagóricos e um dos mais tradicionais são as Fórmulas de Euclides.
Escolhendo-se dois números naturais m>n e os substituindo nas Fórmulas de Euclides a seguir, encontramos os termos a, b e c do Teorema de Pitágoras e consequentemente o Terno Pitagórico.
a = m² - n²
b = 2mn
c = m² + n²
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
Observação 1: as Fórmulas de Euclides geram sequêncialmente ternos pitagóricos primitivos.
Observação 2: as Fórmulas de Euclides não geram sequêncialmente ternos pitagóricos derivados.
As Fórmulas de Euclides geram ternos pitagóricos derivados da seguinte forma: o dobro, do dobro, do dobro, do dobro... e assim sucessivamente de um terno pitagórico primitivo, isto é, multiplicando-se um terno pitagórico primitivo por termos da sequência de potências de base 2: 2, 4, 8, 16, 32, 64, 128,...
Triângulos Retângulos Pitagóricos possuem diversas propriedades algébricas, geométricas, numéricas, métricas e trigonométricas.
O presente estudo demonstra que determinados grupos de Triângulos Retângulos Pitagóricos têm em comum a mesma área, como também, têm o mesmo perímetro.
A tabela a seguir demonstra os 30 primeiros ternos pitagóricos primitivos e derivados gerados sequencialmente pelas Fórmulas de Euclides e, entre eles, os ternos pitagóricos que nas construções de triângulos retângulos, as medidas das áreas são iguais.
| Triângulos Retângulos Pitagóricos | |||||
| de áreas iguais | |||||
| ordem/ | a | b | c | área | perímetro |
| posição | |||||
| 1 | 3 | 4 | 5 | 6 | 12 |
| 2 | 8 | 6 | 10 | 24 | 24 |
| 3 | 5 | 12 | 13 | 30 | 30 |
| 4 | 15 | 8 | 17 | 60 | 40 |
| 5 | 12 | 16 | 20 | 96 | 48 |
| 6 | 7 | 24 | 25 | 84 | 56 |
| 7 | 24 | 10 | 26 | 120 | 60 |
| 8 | 21 | 20 | 29 | 210 | 70 |
| 9 | 16 | 30 | 34 | 240 | 80 |
| 10 | 9 | 40 | 41 | 180 | 90 |
| 11 | 35 | 12 | 37 | 210 | 84 |
| 12 | 32 | 24 | 40 | 384 | 96 |
| 13 | 27 | 36 | 45 | 486 | 108 |
| 14 | 20 | 48 | 52 | 480 | 120 |
| 15 | 11 | 60 | 61 | 330 | 132 |
| 16 | 48 | 14 | 50 | 336 | 112 |
| 17 | 45 | 28 | 53 | 630 | 126 |
| 18 | 40 | 42 | 58 | 840 | 140 |
| 19 | 33 | 56 | 65 | 924 | 154 |
| 20 | 24 | 70 | 74 | 840 | 168 |
| 21 | 13 | 84 | 85 | 546 | 182 |
| 22 | 63 | 16 | 65 | 504 | 144 |
| 23 | 60 | 32 | 68 | 960 | 160 |
| 24 | 55 | 48 | 73 | 1320 | 176 |
| 25 | 48 | 64 | 80 | 1536 | 192 |
| 26 | 39 | 80 | 89 | 1560 | 208 |
| 27 | 28 | 96 | 100 | 1344 | 224 |
| 28 | 15 | 112 | 113 | 840 | 240 |
| 29 | 80 | 18 | 82 | 720 | 180 |
| 30 | 77 | 36 | 85 | 1386 | 198 |
| www.osfantasticosnumerosprimos.com.br | |||||
Os ternos pitagóricos de ordens / posições 2 e 3 são ternos super-especiais, pois são os 2 primeiros ternos pitagóricos a possuirem área e perímetro de mesmo valor.
| ordem / | a | b | c | área | perímetro |
| posição | |||||
| 2 | 8 | 6 | 10 | 24 | 24 |
| 3 | 5 | 12 | 13 | 30 | 30 |
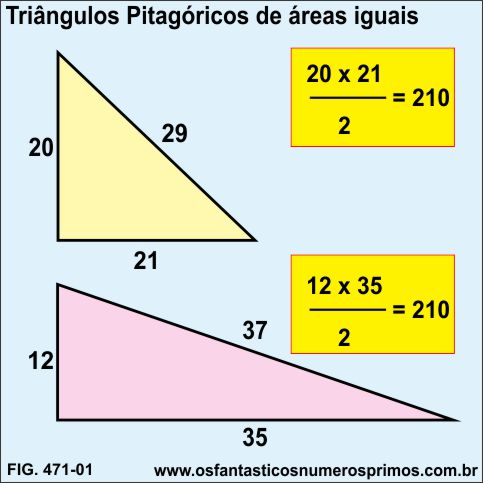
Os ternos pitagóricos de ordens / posições 8 e 11 possuem área de mesmo valor.
| ordem / | a | b | c | área | perímetro |
| posição | |||||
| 8 | 21 | 20 | 29 | 210 | 70 |
| 11 | 35 | 12 | 37 | 210 | 84 |
O Terno Pitagórico Primitivo 20-21-29 é também um terno pitagórico especial, aqui no WebSite, bem como, no livro digital Ternos Pitagóricos e Sequências Numéricas, ele faz parte do grupo de Ternos Pitagóricos Primitivos Raros, isto porque, os termos 20 e 21 são números consecutivos e diferem em 1 unidade.
Estudos realizados e publicados no livro digital Escada de Theon e Sequências Numéricas demonstrou que o algoritimo Escada de Theon gera sequencialmente os Ternos Pitagóricos Primitivos Raros.
Com uso da Calculadora Científica Digital do Software Windows, conseguiu-se calcular até o 140 Terno Pitagórico Primitivo Raro:
31.509.019.100
31.509.019.101
44.560.482.149
Decompondo em Fatores Primos o número 420 que é o dobro de 210, verifica-se que são 24 os divisores de 420.
| Decomposição em Fatores Primos | ||||||||
| do número 420 | ||||||||
| Fatores | Divisores | |||||||
| Primos | ||||||||
| 1 | ||||||||
| 420 | 2 | 2 | ||||||
| 210 | 2 | 4 | ||||||
| 105 | 3 | 3 | 6 | 12 | ||||
| 35 | 5 | 5 | 10 | 15 | 20 | 30 | 60 | |
| 7 | 7 | 7 | 14 | 21 | 28 | 35 | 42 | |
| 1 | 70 | 84 | 105 | 140 | 210 | 420 | ||
D(210)={1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 21, 28, 30, 35, 42, 60, 70, 84, 105, 140, 210, 420}
Elaborando-se pares multiplicativos do produto 420, observa-se que 2 pares multiplicativos são termos dos ternos pitagóricos: 20-21-29 e 12-35-37.
| Pares Multiplicativos | ||||
| do números 420 | ||||
| 1 | x | 420 | = | 420 |
| 2 | x | 210 | = | 420 |
| 3 | x | 140 | = | 420 |
| 4 | x | 105 | = | 420 |
| 5 | x | 84 | = | 420 |
| 6 | x | 70 | = | 420 |
| 7 | x | 60 | = | 420 |
| 10 | x | 42 | = | 420 |
| 12 | x | 35 | = | 420 |
| 14 | x | 30 | = | 420 |
| 15 | x | 28 | = | 420 |
| 20 | x | 21 | = | 420 |
| www.osfantasticosnumerosprimos.com.br | ||||
Os ternos pitagóricos de ordens / posições 18, 20 e 28 possuem área de mesmo valor.
| ordem/ | a | b | c | área | perímetro |
| posição | |||||
| 18 | 40 | 42 | 58 | 840 | 140 |
| 20 | 24 | 70 | 74 | 840 | 168 |
| 28 | 15 | 112 | 113 | 840 | 240 |
O Terno Pitagórico Derivado 40-42-58 é o dobro do terno pitagórico raro 20-21-29.
O Terno Pitagórico Derivado 24-70-74 é o dobro do terno 12-35-37.
O Terno Pitagórico 15-112-113 é primitivo de ordem não triangular.
Os primeiros e segundos termos dos ternos acima formam pares multiplicativos do produto 1680 que é o dobro de 840.
| 24 | x | 70 | = | 1680 |
| 40 | x | 42 | = | 1680 |
| 15 | x | 112 | = | 1680 |
Os ternos pitagóricos de ordens / posições 24 e 46 possuem área de mesmo valor.
| ordem/ | a | b | c | área | perímetro |
| posição | |||||
| 24 | 55 | 48 | 73 | 1320 | 176 |
| 46 | 120 | 22 | 122 | 1320 | 264 |
O Terno Pitagórico 48-55-73 é primitivo de ordem não triangular.
O Terno Pitagórico Derivado 22-120-122 é o dobro do terno primitivo 11-60-61.
Os ternos pitagóricos de ordens / posições 39 e 79 possuem área de mesmo valor.
| ordem/ | a | b | c | área | perímetro |
| posição | |||||
| 39 | 91 | 60 | 109 | 2730 | 260 |
| 79 | 195 | 28 | 197 | 2730 | 420 |
O Terno Pitagórico 60-91-109 é primitivo de ordem não triangular.
O Terno Pitagórico 28-195-197 é primitivo de ordem não triangular.
Entre os 1080 primeiros ternos pitagóricos, encontrou-se:
a) 16 duplas de ternos pitagóricos de mesmas áreas;
b) 5 trincas de ternos pitagóricos de mesmas áreas;
c) 1 quina de ternos pitagóricos de mesmas áreas.
Mais de 90% das áreas têm números terminados em zero (0).
2 áreas têm números terminados em 6 (células liláses).
| Triângulos Pitagóricos | ||
| e áreas iguais | ||
| ordem | áreas | quantidade |
| 1 | 210 | 2 |
| 2 | 210 | |
| 3 | 840 | 3 |
| 4 | 840 | |
| 5 | 840 | |
| 6 | 1320 | 2 |
| 7 | 1320 | |
| 8 | 2730 | 2 |
| 9 | 2730 | |
| 10 | 3360 | 3 |
| 11 | 3360 | |
| 12 | 3360 | |
| 13 | 5280 | 2 |
| 14 | 5280 | |
| 15 | 10920 | 2 |
| 16 | 10920 | |
| 17 | 13440 | 2 |
| 18 | 13440 | |
| 19 | 17010 | 2 |
| 20 | 17010 | |
| 21 | 18480 | 2 |
| 22 | 18480 | |
| 23 | 21120 | 2 |
| 24 | 21120 | |
| 25 | 31920 | 3 |
| 26 | 31920 | |
| 27 | 31920 | |
| 28 | 43680 | 3 |
| 29 | 43680 | |
| 30 | 43680 | |
| 31 | 53760 | 3 |
| 32 | 53760 | |
| 33 | 53760 | |
| 34 | 63360 | 2 |
| 35 | 63360 | |
| 36 | 68040 | 5 |
| 37 | 68040 | |
| 38 | 68040 | |
| 39 | 68040 | |
| 40 | 68040 | |
| 41 | 71610 | 2 |
| 42 | 71610 | |
| 43 | 73920 | 2 |
| 44 | 73920 | |
| 45 | 84480 | 2 |
| 46 | 84480 | |
| 47 | 85470 | 2 |
| 48 | 85470 | |
| 49 | 88536 | 2 |
| 50 | 88536 | |
| 51 | 97440 | 2 |
| 52 | 97440 | |
| www.osfantasticosnumerosprimos.com.br | ||
A tabela a seguir apresenta os 19 primeiros ternos derivados do Terno Pitagórico Primitivo Raro 20-21-29.
Observação importante: devido a limitação de planilha digital para uso em Computador Pessoal, um número com mais de 15 algarismos são representados na forma decimal e com a letra E e o sinal (+)...
Interessante observar que as medidas das áreas são as mesmas da tabela acima: Triângulos Pitagóricos e áreas iguais.
| Terno Pitagórico Primitivo Raro | ||||
| 20-21-29 | ||||
| e derivados | ||||
| ordem / | c | b | a | área |
| posição | ||||
| 8 | 20 | 21 | 29 | 210 |
| 18 | 40 | 42 | 58 | 840 |
| 40 | 80 | 84 | 116 | 3360 |
| 84 | 160 | 168 | 232 | 13440 |
| 179 | 320 | 336 | 464 | 53760 |
| 363 | 640 | 672 | 928 | 215040 |
| 757 | 1280 | 1344 | 1856 | 860160 |
| 2560 | 2688 | 3712 | 3440640 | |
| 5120 | 5376 | 7424 | 13762560 | |
| 10240 | 10752 | 14848 | 55050240 | |
| 20480 | 21504 | 29696 | 220200960 | |
| 40960 | 43008 | 59392 | 880803840 | |
| 81920 | 86016 | 118784 | 3523215360 | |
| 163840 | 172032 | 237568 | 14092861440 | |
| 327680 | 344064 | 475136 | 56371445760 | |
| 655360 | 688128 | 950272 | 2,25486E+11 | |
| 1310720 | 1376256 | 1900544 | 9,01943E+11 | |
| 2621440 | 2752512 | 3801088 | 3,60777E+12 | |
| 5242880 | 5505024 | 7602176 | 1,44311E+13 | |
| 10485760 | 1,1E+07 | 1,5E+07 | 5,77244E+13 | |
| www.osfantasticosnumerosprimos.com.br | ||||
O produto de uma potência de base 2 com 20 e o segundo termo de ternos derivados do terno 20-21-29 tem como resultado a área de um Triângulo Retângulo Pitagórico construído com os mesmos respectivos ternos pitagóricos (excetuando-se o primeiro terno que é um terno primitivo).
| Terno Pitagórico Derivados de | ||||
| 20-21-29 | ||||
| e áreas | ||||
| c | b | a | área | produto de |
| potências base 2 | ||||
| com 20 | ||||
| e segundo termo | ||||
| 20 | 21 | 29 | 210 | ( 1/2 x 20 x 21 ) |
| 40 | 42 | 58 | 840 | ( 2 x 20 x 42 ) |
| 80 | 84 | 116 | 3360 | ( 4 x 20 x 84 ) |
| 160 | 168 | 232 | 13440 | ( 8 x 20 x 168 ) |
| 320 | 336 | 464 | 53760 | ( 16 x 20 x 336 ) |
| 640 | 672 | 928 | 215040 | ( 32 x 20 x 672 ) |
| 1280 | 1344 | 1856 | 860160 | ( 64 x 20 x 1344 ) |
| www.osfantasticosnumerosprimos.com.br | ||||
A multiplicação em diagonal do primeiro termo de um terno antecessor com o segundo termo de um terno sucessor de um terno derivado do Terno Pitagórico Primitivo Raro 20-21-29 tem como resultado a área de um Triângulo Retângulo Pitagórico construído com o respectivo terno pitagórico (excetuando-se o primeiro terno que é um terno primitivo).
| Terno Pitagórico Derivados de | ||||
| 20-21-29 | ||||
| e áreas | ||||
| c | b | a | área | multiplicação |
| em | ||||
| diagonal | ||||
| 10 | ||||
| 20 | 21 | 29 | 210 | ( 10 x 21 ) |
| 40 | 42 | 58 | 840 | ( 20 x 42 ) |
| 80 | 84 | 116 | 3360 | ( 40 x 84 ) |
| 160 | 168 | 232 | 13440 | ( 80 x 168) |
| 320 | 336 | 464 | 53760 | (160 x 336 ) |
| 640 | 672 | 928 | 215040 | ( 320 x 672 ) |
| 1280 | 1344 | 1856 | 860160 | ( 640 x 1344 ) |
| www.osfantasticosnumerosprimos.com.br | ||||
A divisão do segundo termo de ternos derivados do terno 20-21-29 por 7 tem como quociente um múltiplo de 3.
Os múltiplos de 3 formam uma Progressão Geométrica de razão 2: 3, 6, 12, 24, 48,...
Observação importante: a partir deste fato matemático, tem-se um novo método de se gerar o Terno Pitagórico Primitivo Raro 20-21-29 e seus derivados que até então podiam ser gerados por meio de tabelas com as Fórmulas de Euclides e o Algoritmo Escada de Theon.
| Terno Pitagórico Primitivo Raro | ||||
| 20-21-29 | ||||
| e derivados | ||||
| segundo | ||||
| ordem / | c | b | a | termo |
| dividido | ||||
| posição | por 7 | |||
| 8 | 20 | 21 | 29 | 3 |
| 18 | 40 | 42 | 58 | 6 |
| 40 | 80 | 84 | 116 | 12 |
| 84 | 160 | 168 | 232 | 24 |
| 179 | 320 | 336 | 464 | 48 |
| 363 | 640 | 672 | 928 | 96 |
| 757 | 1280 | 1344 | 1856 | 192 |
| 2560 | 2688 | 3712 | 384 | |
| 5120 | 5376 | 7424 | 768 | |
| 10240 | 10752 | 14848 | 1536 | |
| 20480 | 21504 | 29696 | 3072 | |
| 40960 | 43008 | 59392 | 6144 | |
| 81920 | 86016 | 118784 | 12288 | |
| 163840 | 172032 | 237568 | 24576 | |
| 327680 | 344064 | 475136 | 49152 | |
| 655360 | 688128 | 950272 | 98304 | |
| 1310720 | 1376256 | 1900544 | 196608 | |
| 2621440 | 2752512 | 3801088 | 393216 | |
| 5242880 | 5505024 | 7602176 | 786432 | |
| 10485760 | 1,1E+07 | 1,5E+07 | 1572864 | |
| www.osfantasticosnumerosprimos.com.br | ||||
A tabela a seguir apresenta os 19 primeiros ternos derivados do Terno Pitagórico Primitivo 12-35-37.
Observação importante: devido a limitação de planilha digital para uso em Computador Pessoal, um número com mais de 15 algarismos são representados na forma decimal e com a letra E e o sinal (+)...
Interessante observar que as medidas das áreas são as mesmas da tabela acima: Triângulos Pitagóricos e áreas iguais.
| Terno Pitagórico Primitivo | ||||
| 12-35-37 | ||||
| e derivados | ||||
| ordem / | c | b | a | área |
| posição | ||||
| 11 | 12 | 35 | 37 | 210 |
| 20 | 24 | 70 | 74 | 840 |
| 57 | 48 | 140 | 148 | 3360 |
| 88 | 96 | 280 | 296 | 13440 |
| 257 | 192 | 560 | 592 | 53760 |
| 371 | 384 | 1120 | 1184 | 215040 |
| 768 | 2240 | 2368 | 860160 | |
| 1536 | 4480 | 4736 | 3440640 | |
| 3072 | 8960 | 9472 | 13762560 | |
| 6144 | 17920 | 18944 | 55050240 | |
| 12288 | 35840 | 37888 | 2,2E+08 | |
| 24576 | 71680 | 75776 | 8,81E+08 | |
| 49152 | 143360 | 151552 | 3,52E+09 | |
| 98304 | 286720 | 303104 | 1,41E+10 | |
| 196608 | 573440 | 606208 | 5,64E+10 | |
| 393216 | 1146880 | 1212416 | 2,25E+11 | |
| 786432 | 2293760 | 2424832 | 9,02E+11 | |
| 1572864 | 4587520 | 4849664 | 3,61E+12 | |
| 3145728 | 9175040 | 9699328 | 1,44E+13 | |
| 6291456 | 18350080 | 19398656 | 5,77E+13 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Autor: Ricardo Silva - novembro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
SPARKS, John C. The Pythagorean Theorem Crown Jewel of Mathematics. Published by AuthorHouse. Indiana - EUA, 2008

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato