


Triângulos Retângulos Pitagóricos são triângulos retângulos cujos lados são formados por sequências de 3 números inteiros e apresentam relação com o Teorema de Pitágoras, que diz que:
"O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" ou "A soma dos quadrados dos catetos é igual a hipotenusa".
| a² = b² + c² |
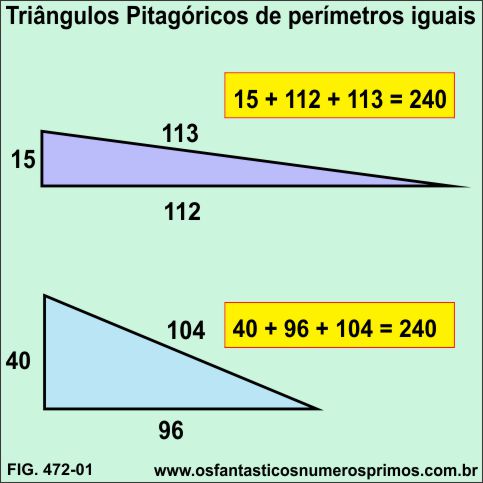
O presente estudo demonstra que determinados grupos de ternos pitagóricos quando da construções de triângulos, os perímetros desses triângulos têm os mesmos valores numéricos.
As Fórmulas de Euclides geram sequêncialmente ternos pitagóricos primitivos, mas não todos os ternos pitagóricos derivados.
Para mais informações, veja abaixo, matérias relacionadas!
A tabela a seguir foi gerada a partir das Fórmulas Euclides.
A tabela apresenta os 58 primeiros ternos pitagóricos primitivos e derivados e, entre eles, os ternos pitagóricos em que os perímetros são iguais.
Os ternos pitagóricos de ordens / posições 2 e 3, são os únicos ternos em um rol de 1080 ternos pesquisados que têm área e perímetro iguais.
| Triângulos Retângulos Pitagóricos | |||||
| de perímetros iguais | |||||
| ordem / | a | b | c | área | perímetro |
| posição | |||||
| 1 | 3 | 4 | 5 | 6 | 12 |
| 2 | 8 | 6 | 10 | 24 | 24 |
| 3 | 5 | 12 | 13 | 30 | 30 |
| 4 | 15 | 8 | 17 | 60 | 40 |
| 5 | 12 | 16 | 20 | 96 | 48 |
| 6 | 7 | 24 | 25 | 84 | 56 |
| 7 | 24 | 10 | 26 | 120 | 60 |
| 8 | 21 | 20 | 29 | 210 | 70 |
| 9 | 16 | 30 | 34 | 240 | 80 |
| 10 | 9 | 40 | 41 | 180 | 90 |
| 11 | 35 | 12 | 37 | 210 | 84 |
| 12 | 32 | 24 | 40 | 384 | 96 |
| 13 | 27 | 36 | 45 | 486 | 108 |
| 14 | 20 | 48 | 52 | 480 | 120 |
| 15 | 11 | 60 | 61 | 330 | 132 |
| 16 | 48 | 14 | 50 | 336 | 112 |
| 17 | 45 | 28 | 53 | 630 | 126 |
| 18 | 40 | 42 | 58 | 840 | 140 |
| 19 | 33 | 56 | 65 | 924 | 154 |
| 20 | 24 | 70 | 74 | 840 | 168 |
| 21 | 13 | 84 | 85 | 546 | 182 |
| 22 | 63 | 16 | 65 | 504 | 144 |
| 23 | 60 | 32 | 68 | 960 | 160 |
| 24 | 55 | 48 | 73 | 1320 | 176 |
| 25 | 48 | 64 | 80 | 1536 | 192 |
| 26 | 39 | 80 | 89 | 1560 | 208 |
| 27 | 28 | 96 | 100 | 1344 | 224 |
| 28 | 15 | 112 | 113 | 840 | 240 |
| 29 | 80 | 18 | 82 | 720 | 180 |
| 30 | 77 | 36 | 85 | 1386 | 198 |
| 31 | 72 | 54 | 90 | 1944 | 216 |
| 32 | 65 | 72 | 97 | 2340 | 234 |
| 33 | 56 | 90 | 106 | 2520 | 252 |
| 34 | 45 | 108 | 117 | 2430 | 270 |
| 35 | 32 | 126 | 130 | 2016 | 288 |
| 36 | 17 | 144 | 145 | 1224 | 306 |
| 37 | 99 | 20 | 101 | 990 | 220 |
| 38 | 96 | 40 | 104 | 1920 | 240 |
| 39 | 91 | 60 | 109 | 2730 | 260 |
| 40 | 84 | 80 | 116 | 3360 | 280 |
| 41 | 75 | 100 | 125 | 3750 | 300 |
| 42 | 64 | 120 | 136 | 3840 | 320 |
| 43 | 51 | 140 | 149 | 3570 | 340 |
| 44 | 36 | 160 | 164 | 2880 | 360 |
| 45 | 19 | 180 | 181 | 1710 | 380 |
| 46 | 120 | 22 | 122 | 1320 | 264 |
| 47 | 117 | 44 | 125 | 2574 | 286 |
| 48 | 112 | 66 | 130 | 3696 | 308 |
| 49 | 105 | 88 | 137 | 4620 | 330 |
| 50 | 96 | 110 | 146 | 5280 | 352 |
| 51 | 85 | 132 | 157 | 5610 | 374 |
| 52 | 72 | 154 | 170 | 5544 | 396 |
| 53 | 57 | 176 | 185 | 5016 | 418 |
| 54 | 40 | 198 | 202 | 3960 | 440 |
| 55 | 21 | 220 | 221 | 2310 | 462 |
| 56 | 143 | 24 | 145 | 1716 | 312 |
| 57 | 140 | 48 | 148 | 3360 | 336 |
| 58 | 135 | 72 | 153 | 4860 | 360 |
| www.osfantasticosnumerosprimos.com.br | |||||
Elaborando-se uma nova tabela somente com as medidas de perímetros, entre os 356 primeiros ternos pitagóricos, verifica-se que há:
a) 24 duplas de ternos pitagóricos com perímetros iguais;
b) 1 trinca de ternos pitagóricos com perímetros iguais.
| Triângulos Pitagóricos | ||
| e grupos de perímetros iguais | ||
| grupos | perímetro | quantidade |
| 1 | 240 | 2 |
| 240 | ||
| 2 | 360 | 2 |
| 360 | ||
| 3 | 480 | 2 |
| 480 | ||
| 4 | 504 | 2 |
| 504 | ||
| 5 | 672 | 2 |
| 672 | ||
| 6 | 720 | 2 |
| 720 | ||
| 7 | 756 | 2 |
| 756 | ||
| 8 | 840 | 2 |
| 840 | ||
| 9 | 864 | 2 |
| 864 | ||
| 10 | 960 | 2 |
| 960 | ||
| 11 | 1008 | 2 |
| 1008 | ||
| 12 | 1080 | 2 |
| 1080 | ||
| 13 | 1188 | 2 |
| 1188 | ||
| 14 | 1200 | 2 |
| 1200 | ||
| 15 | 1260 | 2 |
| 1260 | ||
| 16 | 1320 | 2 |
| 1320 | ||
| 17 | 1344 | 2 |
| 1344 | ||
| 18 | 1400 | 2 |
| 1400 | ||
| 19 | 1440 | 2 |
| 1440 | ||
| 20 | 1512 | 2 |
| 1512 | ||
| 21 | 1560 | 2 |
| 1560 | ||
| 22 | 1584 | 2 |
| 1584 | ||
| 23 | 1680 | 3 |
| 1680 | ||
| 1680 | ||
| 24 | 1728 | 2 |
| 1728 | ||
| 25 | 1848 | 2 |
| 1848 | ||
| www.osfantasticosnumerosprimos.com.br | ||
A tabela a seguir apresenta os 19 primeiros ternos derivados do Terno Pitagórico Primitivo 115-112-113.
Observação importante: devido a limitação de planilha digital para uso em Computador Pessoal, um número com mais de 15 algarismos são representados na forma decimal e com a letra E e o sinal (+)...
Interessante observar que as medidas dos perímetros em destaque são as mesmas da tabela acima: Triângulos Pitagóricos e grupos de perímetros iguais.
| Terno Pitagórico Primitivo | ||||
| 15-112-113 | ||||
| e derivados | ||||
| ordem / | c | b | a | perímetro |
| posição | ||||
| 28 | 15 | 112 | 113 | 240 |
| 92 | 30 | 224 | 226 | 480 |
| 119 | 60 | 448 | 452 | 960 |
| 408 | 120 | 896 | 904 | 1920 |
| 240 | 1792 | 1808 | 3840 | |
| 480 | 3584 | 3616 | 7680 | |
| 960 | 7168 | 7232 | 15360 | |
| 1920 | 14336 | 14464 | 30720 | |
| 3840 | 28672 | 28928 | 61440 | |
| 7680 | 57344 | 57856 | 122880 | |
| 15360 | 114688 | 115712 | 245760 | |
| 30720 | 229376 | 231424 | 491520 | |
| 61440 | 458752 | 462848 | 983040 | |
| 122880 | 917504 | 925696 | 1966080 | |
| 245760 | 1835008 | 1851392 | 3932160 | |
| 491520 | 3670016 | 3702784 | 7864320 | |
| 983040 | 7340032 | 7405568 | 15728640 | |
| 1966080 | 14680064 | 14811136 | 31457280 | |
| 3932160 | 29360128 | 29622272 | 62914560 | |
| 7864320 | 58720256 | 59244544 | 125829120 | |
| www.osfantasticosnumerosprimos.com.br | ||||
A tabela a seguir apresenta os 19 primeiros ternos derivados do Terno Pitagórico Derivado 40-96-104.
Observação importante: devido a limitação de planilha digital para uso em Computador Pessoal, um número com mais de 15 algarismos são representados na forma decimal e com a letra E e o sinal (+)...
Interessante observar que as medidas dos perímetros em destaque são as mesmas da tabela acima: Triângulos Pitagóricos e grupos de perímetros iguais.
| Terno Pitagórico Primitivo | ||||
| 40-96-104 | ||||
| e derivados | ||||
| ordem / | c | b | a | perímetro |
| posição | ||||
| 38 | 15 | 112 | 113 | 240 |
| 63 | 30 | 224 | 226 | 480 |
| 175 | 60 | 448 | 452 | 960 |
| 120 | 896 | 904 | 1920 | |
| 240 | 1792 | 1808 | 3840 | |
| 480 | 3584 | 3616 | 7680 | |
| 960 | 7168 | 7232 | 15360 | |
| 1920 | 14336 | 14464 | 30720 | |
| 3840 | 28672 | 28928 | 61440 | |
| 7680 | 57344 | 57856 | 122880 | |
| 15360 | 114688 | 115712 | 245760 | |
| 30720 | 229376 | 231424 | 491520 | |
| 61440 | 458752 | 462848 | 983040 | |
| 122880 | 917504 | 925696 | 1966080 | |
| 245760 | 1835008 | 1851392 | 3932160 | |
| 491520 | 3670016 | 3702784 | 7864320 | |
| 983040 | 7340032 | 7405568 | 15728640 | |
| 1966080 | 14680064 | 14811136 | 31457280 | |
| 3932160 | 29360128 | 29622272 | 62914560 | |
| 7864320 | 58720256 | 59244544 | 125829120 | |
| www.osfantasticosnumerosprimos.com.br | ||||
No livro The Phytagorean Theorem Crown Jewel of Matematic, pag. 95, do engenheiro aeroespacial estadunidense, John Sparks, se encontra publicado a seguinte tabela com um grupo de 4 ternos pitagóricos cujos perímetros são iguais e faz a seguinte declaração:
"Rarer yet are equal-perimeter Pythagorean Triangles. Table 3.4 shows one set of four equal-perimeter Pythagorean Triangles where the perimeter P <1,000,000. Rumor has it that there are six other sets of four where P< 1,000,000!"
| Triângulos Pitagóricos | |||
| de perímetros iguais | |||
| a | b | c | perímetros |
| 153868 | 9435 | 154157 | 317460 |
| 99660 | 86099 | 131701 | 317460 |
| 43660 | 133419 | 140381 | 317460 |
| 13260 | 151811 | 152389 | 317460 |
Fonte: adaptado de: SPARKS, John C. The Pythagorean Theorem Crown Jewel of Mathematics.
Realizando os cálculos com o Teorema de Pitágoras, confirma-que os valores das hipotenusas com os termos (c) da tabela acima.
Um detalhe interessante é que os valores das hipotenusas são todos números primos.
| quadrado | quadrado | soma | raiz |
| cateto | cateto | quadrados | quadrada |
| catetos | |||
| hipotenusa | |||
| 89019225 | 23675361424 | 23764380649 | 154157 |
| 7413037801 | 9932115600 | 17345153401 | 131701 |
| 17800629561 | 1906195600 | 19706825161 | 140381 |
| 23046579721 | 175827600 | 23222407321 | 152389 |
Presume-se que o engenheiro aeroespacial John Sparks, tenha produzido tabelas semelhantes às publicadas neste estudo e no estudo: 011-estudos-471-triangulos-pitagoricos-de-areas-iguais, isto porque, variando-se os termos m > n de 100 em 100 para se gerarem ternos pitagóricos, na linha 300 > 299, chega-se a perímetro de medida 359.400 que está na faixa dos 317.460.
| Ternos Pitagóricos | ||||||
| m | n | a | b | c | area | perimetro |
| 100 | 99 | 199 | 19800 | 19801 | 1970100 | 39800 |
| 200 | 199 | 399 | 79600 | 79601 | 15880200 | 159600 |
| 300 | 299 | 599 | 179400 | 179401 | 53730300 | 359400 |
| 400 | 399 | 799 | 319200 | 319201 | 1,28E+08 | 639200 |
| 500 | 499 | 999 | 499000 | 499001 | 2,49E+08 | 999000 |
| 600 | 599 | 1199 | 718800 | 718801 | 4,31E+08 | 1438800 |
| 700 | 699 | 1399 | 978600 | 978601 | 6,85E+08 | 1958600 |
| 800 | 799 | 1599 | 1278400 | 1278401 | 1,02E+09 | 2558400 |
| 900 | 899 | 1799 | 1618200 | 1618201 | 1,46E+09 | 3238200 |
| 1000 | 999 | 1999 | 1998000 | 1998001 | 2E+09 | 3998000 |
| 1100 | 1099 | 2199 | 2417800 | 2417801 | 2,66E+09 | 4837800 |
| 1200 | 1199 | 2399 | 2877600 | 2877601 | 3,45E+09 | 5757600 |
| www.osfantasticosnumerosprimos.com.br | ||||||
Efetuando-se os cálculos de uma soma de uma progressão aritmética (P.A.)...
| (1 + 400) | ||||
| S400 | = | _________ | x | 400 |
| 2 |
... chega-se 80.200 que deve ter sido a quantidade de linhas da tabela que o engenheiro aeroespacial Sparks produzira.
Lembrando que os ternos derivados vão aumentando em progressão geométrica de razão 2.
"Triângulos Pitagóricos Isoperimétricos são triângulos de mesmo perímetro e áreas diferentes".
Os estudos de Triângulos Pitagóricos Isoperimétricos se encontram publicados na obra: Desvendando os Segredos do Triângulo Retângulo e Descobrindo Curiosidades até hoje não Conhecidas, do Professor Sebastião Vieira do Nascimento, carinhosamente conhecido por Professor Sebá.
Vejamos um exemplo, na pagina 35, da referida obra do Professor Sebá.
Quantos triângulos pitagóricos isoperimétricos existem com perímeto (P) igual a 240m?
Resolução:
Os valores de k são dados pelos divisores de P no intervalo:
| 5 P | P | ||
| 1 ≤ k < | ___ | - | __ |
| 12 | 4 |
Neste intervalo podem existir dois ou mais triângulos pitagóricos isoperimétricos. Entre todos os triângulos pitagóricos que existem, o de mair dimensão é o triângulo pitagórico de lados:
| P | ||
| a | = | __ |
| 4 |
| P | ||
| b | = | __ |
| 3 |
e
| 5 P | ||
| c | = | __ |
| 12 |
Se existirem outros triângulos pitagóricos com
| P | = | 240 |
então,
| 5 P | P | |||||
| c - b | = | k | < | ___ | - | __ |
| 12 | 4 |
Como
| P | = | 240 |
logo,
| 240 | ||||
| a | = | ___ | = | 60 |
| 4 |
| 240 | ||||
| b | = | ___ | = | 80 |
| 3 |
| 5 x 240 | ||||
| a | = | ___ | = | 100 |
| 12 |
Perímetro: 60 m + 80 m + 100 m = 240 m
Já que
c - b = k
100 - 80 = 20
logo, o intervalo para k é:
| 1 ≤ k < 20 |
Como os divisores de 240 < 20 são:
1, 2, 3, 4, 5, 6, 8, 10, 12 e 16, logo,
k = 1, 2, 3, 4, 5, 6, 8, 10, 12 ou 16.
Para k = 1
| - 1 + √1 ( 1 + 4 x 240 ) | ||||
| a | = | __________________ | = | 15 |
| 2 |
| 15² + 1² | ||||
| c | = | __________________ | = | 113 |
| 2 x 1 |
e
b = c - k
113 - 1 = 112
(a, b, c) = (15, 112, 113)
Perímetro: 15 m + 112 m + 113 m = 240 m
Para K = 2
| - 2 + √2 ( 2 + 4 x 240 ) | ||||
| a | = | __________________ | = | 10,46 |
| 2 |
(Não é cateto menor de um triângulo pitagórico)
Após testar os restantes ks, para k no intervalo:
| 3 ≤ k < 20 |
obteve-se os seguintes resultado para k = 8 e 12:
Para K = 8
| - 8 + √8 ( 8 + 4 x 240 ) | ||||
| a | = | __________________ | = | 40 |
| 2 |
Cálculo da hipotenusa (c) e do cateto mairo (b) para a = 40:
| 40² + 8² | ||||
| c | = | __________________ | = | 104 |
| 2 x 8 |
e
b = c - k
104 - 8 = 96
Perímetro: 40 m + 96 m + 104 m = 240 m
Para K = 12
| - 12 + √12 ( 12 + 4 x 240 ) | ||||
| a | = | __________________ | = | 48 |
| 2 |
Cálculo da hipotenusa (c) e do cateto maior (b) para a = 48:
| 48² + 12² | ||||
| c | = | __________________ | = | 102 |
| 2 x 12 |
e
b = c - k
102 - 12 = 90
Perímetro: 48 m + 90 m + 102 m = 240 m
Resposta: Para um perímetro igual a 240 m, existem quatro triângulos retângulos pitagóricos isoperimétricos:
| Cateto Menor | Cateto Maior | Hipotenusa | área m² | perímetro |
| 60 | 80 | 100 | 2400 | 240 |
| 15 | 112 | 113 | 840 | 240 |
| 40 | 96 | 104 | 1920 | 240 |
| 48 | 90 | 102 | 2160 | 240 |
Fonte: adaptado de Desvendando os Segredos do Triângulo Retângulo e Descobrindo Curiosidades até hoje não Conhecidas.
Conclusão
Com um perímetro (15 m, 112 m, 113 m), obteve-se uma área de 840 m². Com o mesmo perímetro (60m, 80m, 100m), obteve-se uma área de 2400 m², ou seja, uma área quase três vezes maior.
Observação muito importante:
Como reiterado neste estudo e em outros publicados aqui no WebSite, bem como, no livro digital Ternos Pitagóricos e Sequências Numéricas, as Fórmulas de Euclides não geram todos os ternos pitagóricos derivados.
Analisando a tabela:
| Triângulos Retângulos Pitagóricos | |||||
| de perímetros iguais | |||||
| ordem / | a | b | c | área | perímetro |
| posição | |||||
| 28 | 15 | 112 | 113 | 840 | 240 |
| 38 | 96 | 40 | 104 | 1920 | 240 |
| www.osfantasticosnumerosprimos.com.br | |||||
constata-se que somente os ternos: 15-112-113 e 96-40-104 aparecem na tabela.
Os ternos: 48-90-102 e 60-80-100 não aparecem na tabela, pois, as Fórmulas de Euclides não conseguem gerá-los.
O terno 48-90-102 é derivado do terno primitivo 8-15-17 da seguinte forma:
6 x 8 = 48
6 x 15 = 90
6 x 17 = 102
O terno 60-80-100 é derivado do terno primitivo 3-4-5 da seguinte forma:
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
Os fatores 6 e 20 não são potências de base 2, portanto, os ternos não são os dobros, dos dobros, do dobros... dos ternos pitagóricos primitivos: 3-4-5 e 8-15-17.
As Fórmulas Isoperimétricas do Professor Sebá conseguiu gerar os ternos pitagóricos gerados e não gerados pelas Fórmulas de Euclides cujos perímetros são iguais, isto é, 240.
Autor: Ricardo Silva - novembro/2023
NASCIMENTO, Sebastião Vieira do. Desvendando os Segredos do Triângulo Retângulo e Descobrindo Curiosidades até hoje não Conhecidas / Sebastião Vieira do Nascimento. - Rio de Janeiro: Gramma, 2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
SPARKS, John C. The Pythagorean Theorem Crown Jewel of Mathematics. Published by AuthorHouse. Indiana - EUA, 2008

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato