


Não tenha dúvida, que teclar [ 2 ] e em seguida teclar o símbolo da raiz quadrada [ √ ] em dispositivos digitais, como: calculadoras, calculadoras em computadores, calculadoras em telefones celulares, etc... tenhamos o belíssissímo resultado (as casas decimais depende do dispositivo!):
a raiz quadrada de 2...
1,414
um número decimal, não periódico e infinito.
E tentar fazer os cálculos manual e mentalmente, já pensou nisto?
E o número 1024, qual é sua raiz quadrada?
Dica: é par, termina em 4 e está instrinsecamente relacionado ao mundo da informática, dos bits e dos bytes.
Não, não é fácil de se extrair raiz quadrada manual e mentalmente, para números pequenos sim, por exemplo, o número 100, por meio da:
Decomposição em fatores primos
| Decomposição em fatores primos | |
| número 100 | |
| Fatores Primos | |
| 100 | 2 |
| 50 | 2 |
| 25 | 5 |
| 5 | 5 |
| 1 | |
| www.osfantasticosnumerosprimos.com.br | |
√100 =
= √2².5²
= 2.5
= 10
Foi a partir do número quadrado perfeito 100 que a Pequena Grande Júlia Pimenta Ferreira, de 11 anos, descobriu a raiz quadrada do número 144.
Para mais informações, veja abaixo, matérias relacionadas!
Este estudo é uma homenagem a todos que descobrem, redescobrem e continuam redescobrindo a maravilhosa Matemática.
Todo número natural é a raiz quadrada de um outro número natural, mas nem todo natural é um quadrado perfeito, um cubo perfeito, um número de quarta, quinta, sexta potência e assim por diante.
Número Quadrado Perfeito é um número que é produto de um número natural por ele mesmo e quando extraído a raiz quadrada, o resultado é esse mesmo número natural.
Números quadrados perfeitos terminam em 1, 4, 5, 6, 9 ou 0.
Não há números quadrados perfeitos que terminam em 2, 3, 7 ou 8.
A seguinte tabela apresenta os 20 primeiros números naturais (raízes), seus respectivos quadrados perfeitos, bem como, a diferença entre dois quadrados e diferença entre duas raízes.
A diferença entre dois números quadrados perfeitos consecutivos tem como resultado um número ímpar.
A diferença entre números quadrados perfeitos formam a sequência de números ímpares a partir do número 3: 3, 5, 9, 11, 13,...
| Diferença entre | ||
| números quadrados perfeitos | ||
| Diferença de quadrados | ||
| Número | Quadrado | Ímpares |
| (raiz) | ||
| 1 | 1 | |
| (1) | 3 | |
| 2 | 4 | |
| (1) | 5 | |
| 3 | 9 | |
| (1) | 7 | |
| 4 | 16 | |
| (1) | 9 | |
| 5 | 25 | |
| (1) | 11 | |
| 6 | 36 | |
| (1) | 13 | |
| 7 | 49 | |
| (1) | 15 | |
| 8 | 64 | |
| (1) | 17 | |
| 9 | 81 | |
| (1) | 19 | |
| 10 | 100 | |
| (1) | 21 | |
| 11 | 121 | |
| (1) | 23 | |
| 12 | 144 | |
| (1) | 25 | |
| 13 | 169 | |
| (1) | 27 | |
| 14 | 196 | |
| (1) | 29 | |
| 15 | 225 | |
| (1) | 31 | |
| 16 | 256 | |
| (1) | 33 | |
| 17 | 289 | |
| (1) | 35 | |
| 18 | 324 | |
| (1) | 37 | |
| 19 | 361 | |
| (1) | 39 | |
| 20 | 400 | |
| www.osfantasticosnumerosprimos.com.br | ||
Podemos facilmente comprovar as raízes quadradas entre dois números quadrados consecutivos, pois:
A diferença entre dois números quadrados perfeitos consecutivos é um número ímpar.
Um número ímpar igual ou maior que 3 é a diferença entre dois números quadrados perfeitos consecutivos.
A soma de dois números consecutivos é igual a diferença entre dois números quadrados perfeitos consecutivos.
A soma de dois números consecutivos é um número ímpar e esses dois números consecutivos são as raízes quadradas dos quadrados cujo o número ímpar é a diferença.
Para mais informações, veja abaixo, matérias relacionadas!
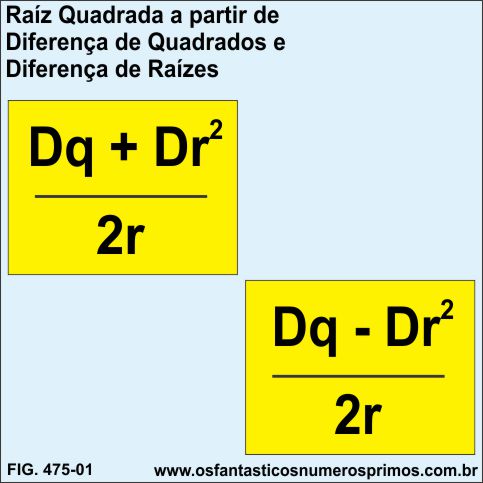
Por meio das seguintes fórmulas, onde:
Dq = Diferença entre dois quadrados perfeitos
Dr² = Diferença entre duas raízes ao quadrado
2r = Dobro da diferença entre duas raízes
podem ser comprovadas:
a) a raiz quadrada sucessora - Fórmula da Soma
| Dq + Dr² |
| ____ |
| 2 x r |
b) a raiz quadrada antecessora - Fórmula da Diferença
| Dq - Dr² |
| ____ |
| 2 x r |
| Diferença de quadrados | ||
| Número | Quadrado | Ímpares |
| (raiz) | ||
| 2 | 4 | |
| (1) | (5) | |
| 3 | 9 |
A diferença das raízes ao quadrado (1²) subtraida da diferença dos quadrados (5) e dividida pelo dobro da diferença da raízes têm como quociente a √4 = 2.
| 5 - 1² | 4 | |||
| ____ | = | ___ | = | 2 |
| 2 x 1 | 2 |
A diferença das raízes ao quadrado (1²) somada a diferença dos quadrados (5) e dividida pelo dobro da diferença da raízes têm como quociente a √9 = 3.
| 5 + 1² | 6 | |||
| ____ | = | ___ | = | 3 |
| 2 x 1 | 2 |
| Diferença de quadrados | ||
| Número | Quadrado | Ímpares |
| (raiz) | ||
| 4 | 16 | |
| (1) | (9) | |
| 5 | 25 |
A diferença das raízes ao quadrado (1²) subtraída da diferença dos quadrados (9) e dividida pelo dobro da diferença da raízes têm como quociente a √16 = 4.
| 9 - 1² | 8 | |||
| ____ | = | ___ | = | 4 |
| 2 x 1 | 2 |
A diferença das raízes ao quadrado (1²) somada a diferença dos quadrados (9) e dividida pelo dobro da diferença da raízes têm como quociente a √25 = 5.
| 9 + 1² | 10 | |||
| ____ | = | ___ | = | 5 |
| 2 x 1 | 2 |
Observação importante 1: nos exemplos acima, as raízes quadradas são números consecutivos.
Observação importante 2 : nos exemplos demonstrados acima, fez se o uso da Tabela Diferença entre Números Quadrados Perfeitos para substituir os valores dos quadrados, bem como, suas diferenças e as diferenças das raízes nas fórmulas acima e os demais cálculos foram realizados manualmente.
Podemos facilmente comprovar as raízes quadradas entre dois quadrados não consecutivos.
| Diferença de quadrados | ||
| Número | Quadrado | Ímpares |
| (raiz) | ||
| 5 | 25 | |
| (3) | (39) | |
| 8 | 64 |
A diferença das raízes ao quadrado (3²) subtraída da diferença dos quadrados (39) e dividida pelo dobro da diferença da raízes têm como quociente a √25 = 5.
| 39 - 3² | 30 | |||
| ____ | = | ___ | = | 5 |
| 2 x 3 | 6 |
A diferença das raízes ao quadrado (1²) somada a diferença dos quadrados (39) e dividida pelo dobro da diferença da raízes têm como quociente a √64 = 8.
| 39 + 3² | 48 | |||
| ____ | = | ___ | = | 8 |
| 2 x 3 | 6 |
| Diferença de quadrados | ||
| Número | Quadrado | Ímpares |
| (raiz) | ||
| 3 | 9 | |
| (13) | (247) | |
| 16 | 256 |
A diferença das raízes ao quadrado (13²) subtraída da diferença dos quadrados (247) e dividida pelo dobro da diferença da raízes têm como quociente a √9 = 3.
| 247 - 13² | 78 | |||
| ____ | = | ___ | = | 3 |
| 2 x 13 | 26 |
A diferença das raízes ao quadrado (13²) somada a diferença dos quadrados (247) e dividida pelo dobro da diferença da raízes têm como quociente a √256 = 16.
| 247 + 13² | 416 | |||
| ____ | = | ___ | = | 16 |
| 2 x 13 | 26 |
Observação importante 1: nos exemplos acima, as raízes quadradas não são números consecutivos.
Observação importante 2: nos exemplos demonstrados acima, fez se o uso da Tabela Diferença entre Números quadrados Perfeitos para substituir os valores dos quadrados, bem como, suas diferenças e as diferenças das raízes nas fórmulas acima e os demais cálculos foram realizados manualmente.
Escolhendo se números aleatórios (supostos quadrados), qual a chance de se obter todos os resultados números inteiros?
Os exemplos a seguir foram cálculados fazendo-se o uso das Fórmulas acima em planilha digital e inserindo somente números quadrados perfeitos consecutivos, comprovando-se assim as respectivas raízes quadradas.
| Diferença | Diferença | ||
| raiz | quadrados | quadrados | raízes |
| 10 | 100 | ||
| 21 | 1 | ||
| 11 | 121 | ||
| soma | 11 | ||
| diferença | 10 |
| Diferença | Diferença | ||
| raiz | quadrados | quadrados | raízes |
| 25 | 625 | ||
| 51 | 1 | ||
| 26 | 676 | ||
| soma | 26 | ||
| diferença | 25 |
Os exemplos a seguir foram calculados fazendo-se o uso das Fórmulas acima em planilha digital e inserindo somente números aleatórios nas respectivas células para números quadrados perfeitos e fazendo se estimativas entre quadrados e raízes.
Escolhendo-se os "supostos quadrados", os resultados não são números inteiros.
Exemplo 1)
Um "suposto quadrado" terminado em 0 (zero).
| Diferença | Diferença | ||
| raiz | quadrados | quadrados | raízes |
| 47,95832 | 2300 | ||
| 90 | 0,929311 | ||
| 48,88763 | 2390 | ||
| soma | 42,22028 | ||
| diferença | 41,41771 |
Exemplo 2)
Um "suposto quadrado" terminado em 5 (zero).
| Diferença | Diferença | ||
| raiz | quadrados | quadrados | raízes |
| 73,85797 | 5455 | ||
| 147 | 0,988538 | ||
| 74,84651 | 5602 | ||
| soma | 73,14053 | ||
| diferença | 72,17452 |
Exemplo 3)
Um "suposto quadrado" terminado em 6 (zero).
Somou-se um "suposto consecutivo" 331 e o quadrado imperfeito 110117 terminado em 7.
Não há quadrado perfeito que termina em 7.
| Diferença | Diferença | ||
| raiz | quadrados | quadrados | raízes |
| 330,8414 | 109456 | ||
| 661 | 0,997464587 | ||
| 331,8388 | 110117 | ||
| soma | 330,1583 | ||
| diferença | 329,1658 |
Nos 3 exemplos acima escolheu-se números aleatórios e os resultados não foram números inteiros.
Autor: Ricardo Silva - novembro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato