


A soma de algarismos de números revelam interessantes propriedades matemáticas, estudos publicados aqui no WebSite Os Fantásticos Números Primos, bem como, nos livros digitais: Os Fantásticos Números Primos e Estudos de Sequências Numéricas, demonstram que escolhendo quaisquer números de 2 ou mais algarismos, somando esses algarismos e subtraindo a soma dos algarismos desse número, a diferença é um número múltiplo / divisor de 3 e de 9.

Exemplos:
a)
17
1 + 7 = 8
17 - 8 = 9
9 é divisível por 3 e por 9
b)
55
5 + 5 = 10
55 - 10 = 45
45 é divisível por 3 e por 9
c)
148
1 + 4 + 8 = 13
148 - 13 = 135
135 é divisível por 3 e por 9
No critério de divisibilidade por 3, se a soma dos algarismos de um número for divisível por 3, então esse número é divisível por 3. O mesmo método é utilizado para se saber se um número também é ou não divisível por 9.
A raiz digital de um número são adições sucessivas dos algarismos de um número até se ter como resultado um número de único algarismo.
Exemplo:
123456789
passo 1)
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
passo 2)
4 + 5 = 9
9 é a raiz digital do número 123456789.
Noves Fora é um método se saber se determinado número é ou não um múltiplo de 9, o mesmo que saber o resto da divisão por 9.
Exemplo 1)
10 : 9 = 1 e o resto da divisão é 1
somando os algarismos do número 10
1 + 0 = 1
1 é o resto da divisão de 10 por 9
Exemplo 2)
43 : 9 = 4 e o resto da divisão é 7
somando os algarismos do número 43
4 + 3 = 7
7 é o resto da divisão de 43 por 9
Noves Fora é também um método para se comprovar a exatidão de operações de adição, subtração, multiplicação ou divisão.
431 + 256 = 687
passo 1)
somam-se os algarismos da primeira parcela (431)
4 + 3 + 1 = 8 (um só algarismo, ok)
passo 2)
somam-se os algarismos da segunda parcela (256)
2 + 5 + 6 = 13 (dois algarismos)
passo 3)
soma-se os algarismos do total 13
1 + 3 = 4 (um só algarismo, ok)
passo 4)
somam-se os algarismos resultantes das parcelas
8 + 4 = 12 (dois algarismos)
passo 5)
somam-se os algarismos do total 12
o resultado é 3
1 + 2 = 3 (um só algarismo, ok)
passo 6)
somam-se os algarismos do total (687)
6 + 8 + 7 = 21 (dois algarismos)
passo 7)
soma-se os algarismos do total 21
2 + 1 = 3 (um só algarismo, ok)
Os algarismos resultantes das parcelas e do total tem um mesmo resultado: 3, comprovando-se assim que a operação de adição acima está correta.
O exemplo a seguir foi extraído do WebSite:
mestredoconhecimento.forumeiros.com
datado de 16/02/2017.
O autor se denomina Alquimista e expõe estudos relacionando simetrias do Quadrados Sator com um Quadrado Mágico 9x9.
O autor na introdução de seu estudo faz a seguinte afirmação:
"Quadrados Mágicos são aqueles formados por números inteiros distintos em que a soma dos algarismos
das diagonais, colunas e linhas levam a um mesmo resultado.
Tudo o que será apresentado neste estudo é válido para todos os Quadrados Mágicos Verdadeiros, ou
seja, aqueles que seguem todas as propriedades citadas acima.
O conceito de simetria utilizado por MIM quando me refiro às casas do quadrado mágico é de um tipo
espelhado, invertido, similar a como se encontram as letras iguais no quadrado Sator, portanto, evitem
fazer confusões.
Quadrados Mágicos são aqueles em que a soma dos algarismos de suas diagonais, colunas e linhas levam
a um mesmo resultado, que é um número chamado de constante ou número planetário.
Consideremos o seguinte Quadrado Mágico do tipo 9x9:"
Para mais informações de como construir quadrado mágico 9x9 e também outras propriedades numéricas, veja:
011-estudos-197-quadrados-magicos-9x9
O Quadrado Mágico 9x9 utilizado pelo Alquimista em seus estudos tem como método de construção o Método Moschopoulos 1, descrito no livro Magic Square de Holger Danielsson (edição - março de 2022), pag. 106.
Observações:
a) na diagonal principal, encontram-se os números 37, 38, 39, 40, 41, 42, 43, 44 e 45 sequencialmente;
b) na célula central, o número 41, média aritmética da soma de 1 com 81;
c) o número 1 se encontra abaixo do número 41.
d) o número 9 se encontra ao lado do número 41;
e) o número 81 se encontra acima do número 41.
| Quadrado Mágico 9x9 | ||||||||||
| 369 | ||||||||||
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5 | 369 | |
| 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46 | 369 | |
| 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15 | 369 | |
| 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56 | 369 | |
| 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25 | 369 | |
| 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66 | 369 | |
| 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35 | 369 | |
| 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76 | 369 | |
| 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45 | 369 | |
| 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | |
Fonte: adaptado de:
https://mestredoconhecimento.forumeiros.com
No estudo realizado pelo Alquimista, o diferencial são as conversões dos números do Quadrado Mágico 9x9 em raízes digitais perfeitas e que apresentam, entre outras, propriedades como:
a) a soma de cada linha, cada coluna e diagonais é 45;
b) a diagonal principal (amarela) é formada por números de 1 a 9 sequencialente;
c) a diagonal secundária (laranja) é formada por números 5;
5 é a média aritmética da soma de 1 com 9;
d) nas diagonais quebradas paralelas à secundária, os números são os mesmos, formando palíndromos;
e) as diagonais quebradas paralelas à principal, os números estão equidistantes;
f) os números não se repetem em linhas e colunas (como no Passatempo Sudoku).
| Quadrado Mágico 9x9 | ||||||||||
| convertido em raízes digitais | ||||||||||
| 45 | ||||||||||
| 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 | 5 | 45 | |
| 6 | 2 | 7 | 3 | 8 | 4 | 9 | 5 | 1 | 45 | |
| 2 | 7 | 3 | 8 | 4 | 9 | 5 | 1 | 6 | 45 | |
| 7 | 3 | 8 | 4 | 9 | 5 | 1 | 6 | 2 | 45 | |
| 3 | 8 | 4 | 9 | 5 | 1 | 6 | 2 | 7 | 45 | |
| 8 | 4 | 9 | 5 | 1 | 6 | 2 | 7 | 3 | 45 | |
| 4 | 9 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 45 | |
| 9 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 45 | |
| 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 | 45 | |
| 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 | |
Fonte: adaptado de:
https://mestredoconhecimento.forumeiros.com
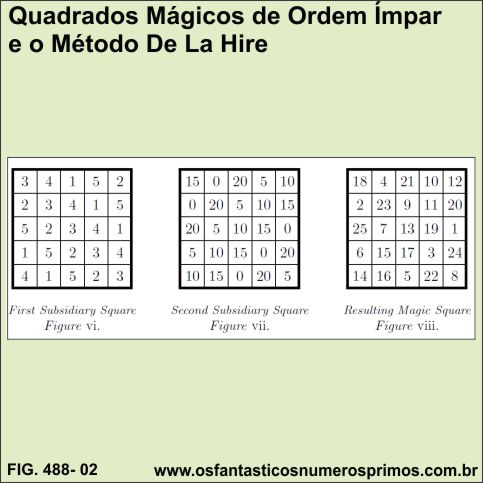
Interessante observar que o Quadrado Mágico 9x9 convertidos em raízes digitais perfeitas se assemelha a quadrado auxiliar para construções de quadrados mágicos de ordem ímpar do Método De La Hire, conforme publicado na obra: Mathematical Recreations and Essays, pag. 126 de W. W. Rouse Ball - Outubro 8, 2008 [EBook #26839] do Projeto Gutenberg.
Observação importante: no exemplo do Método De La Hire, no primeiro quadrado auxiliar, o termo médio 3 da sequência (1, 2, 3, 4, 5) se encontra na diagonal principal e no segundo quadrado, o termo médio 10 da sequência dos múltiplos de 5 (0, 5, 10, 15, 20) se encontra na digonal secundária.
Construindo o segundo quadrado auxiliar com os múltiplos de 9: 0, 9, 18, 27, 36, 45, 54, 63 e 72 em que a diagonal secundária é formada pelo termo médio 36 e...
| Quadrado Auxiliar 9x9 | ||||||||||
| com múltiplos de 9 | ||||||||||
| 324 | ||||||||||
| 36 | 9 | 18 | 27 | 0 | 45 | 54 | 63 | 72 | 324 | |
| 72 | 36 | 9 | 18 | 27 | 0 | 45 | 54 | 63 | 324 | |
| 63 | 72 | 36 | 9 | 18 | 27 | 0 | 45 | 54 | 324 | |
| 54 | 63 | 72 | 36 | 9 | 18 | 27 | 0 | 45 | 324 | |
| 45 | 54 | 63 | 72 | 36 | 9 | 18 | 27 | 0 | 324 | |
| 0 | 45 | 54 | 63 | 72 | 36 | 9 | 18 | 27 | 324 | |
| 27 | 0 | 45 | 54 | 63 | 72 | 36 | 9 | 18 | 324 | |
| 18 | 27 | 0 | 45 | 54 | 63 | 72 | 36 | 9 | 324 | |
| 9 | 18 | 27 | 0 | 45 | 54 | 63 | 72 | 36 | 324 | |
| 324 | 324 | 324 | 324 | 324 | 324 | 324 | 324 | 324 | 324 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
...somando-se os termos correspondentes referente à cada célula, obtem-se um outro Quadrado Mágico 9x9.
Interessante observar que:
a) na célula central se encontra o número 41 que a média aritmética de (1 + 81) / 2 = 41;
b) na diagonal principal encontram-se sequencialmente os números 37, 38, 39, 40, 41, 42, 43, 44 e 45 .
c) o número 1 se encontra a 3 células abaixo e a 3 células à esquerda do número 41;
d) o número 9 se encontra à esquerda superior do número 1;
e) o número 91 se encontra à esquerda do número 41;
f) a constante mágica é 369.
| Quadrado Mágico 9x9 | ||||||||||
| 369 | ||||||||||
| 37 | 15 | 20 | 34 | 3 | 53 | 58 | 72 | 77 | 369 | |
| 78 | 38 | 16 | 21 | 35 | 4 | 54 | 59 | 64 | 369 | |
| 65 | 79 | 39 | 17 | 22 | 36 | 5 | 46 | 60 | 369 | |
| 61 | 66 | 80 | 40 | 18 | 23 | 28 | 6 | 47 | 369 | |
| 48 | 62 | 67 | 81 | 41 | 10 | 24 | 29 | 7 | 369 | |
| 8 | 49 | 63 | 68 | 73 | 42 | 11 | 25 | 30 | 369 | |
| 31 | 9 | 50 | 55 | 69 | 74 | 43 | 12 | 26 | 369 | |
| 27 | 32 | 1 | 51 | 56 | 70 | 75 | 44 | 13 | 369 | |
| 14 | 19 | 33 | 2 | 52 | 57 | 71 | 76 | 45 | 369 | |
| 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
Citando novamente a afirmação do Alquimista do WebSite:
https://mestredoconhecimento.forumeiros.com
"Quadrados Mágicos são aqueles formados por números inteiros distintos em que a soma dos algarismos
das diagonais, colunas e linhas levam a um mesmo resultado.
Tudo o que será apresentado neste estudo é válido para todos os Quadrados Mágicos Verdadeiros, ou
seja, aqueles que seguem todas as propriedades citadas acima."
Realizando testes com quadrados mágicos apresentados abaixo, contata-se que a afirmação do Alquimista não está correta, pois, os quadrados mágicos, a seguir, convertidos em raízes digitais, apresentam somas de linhas, colunas e diagonais valores diferentes, não formando "Constante Mágica" como a do Quadrado 9x9 convertido em raízes digitais perfeitas.
| Quadrado Mágico 3x3 | ||||
| Lo-shu | ||||
| 15 | ||||
| 4 | 9 | 2 | 15 | |
| 3 | 5 | 7 | 15 | |
| 8 | 1 | 6 | 15 | |
| 15 | 15 | 15 | 15 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Podemos dizer que o Quadrado Mágico 3x3 (Lo-Shu) é um quadrado diferenciado, pois, seus números já são formados por algarismos unitários.
Quadrado Auxiliar com múltiplos de 3 começando por 0 (zero): 0, 3, 6.
| Quadrado Auxiliar 3x3 (1) | ||||
| com múltiplos de 3 | ||||
| 9 | ||||
| 0 | 6 | 3 | 9 | |
| 6 | 3 | 0 | 9 | |
| 3 | 0 | 6 | 9 | |
| 9 | 9 | 9 | 9 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Somando-se células correspondentes do Quadrado Mágico 3x3 (Lo-Shu) com as do Quadrado Auxiliar 3x3 (1) , obtem-se "Constante Mágica 24".
Importante observar que a sequência: 1, 4, 5, 7, 8, 9, 11, 12, 15 não forma uma progressão aritmética (P.A.) e mesmo assim produz a constante mágica 24.
| Quadrado Resultante 3x3 (1) | ||||
| com múltiplos de 3 | ||||
| 24 | ||||
| 4 | 15 | 5 | 24 | |
| 9 | 8 | 7 | 24 | |
| 11 | 1 | 12 | 24 | |
| 24 | 24 | 24 | 24 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Quadrado Auxiliar com múltiplos de 3 começando por 3: 3, 6, 9.
| Quadrado Auxiliar 3x3 (2) | ||||
| com múltiplos de 3 | ||||
| 18 | ||||
| 3 | 9 | 6 | 18 | |
| 9 | 6 | 3 | 18 | |
| 6 | 3 | 9 | 18 | |
| 18 | 18 | 18 | 18 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Somando-se células correspondentes do Quadrado Mágico 3x3 (Lo-Shu) com as do Quadrado Auxiliar 3x3 (2), obtem-se "Constante Mágica 33".
Importante observar que a sequência: 4, 7, 8, 10, 11, 12, 14, 15, 18 não forma uma progressão aritmética (P.A.) e mesmo assim produz constante mágica 33.
| Quadrado Resultante 3x3 (2) | ||||
| 33 | ||||
| 7 | 18 | 8 | 33 | |
| 12 | 11 | 10 | 33 | |
| 14 | 4 | 15 | 33 | |
| 33 | 33 | 33 | 33 | |
| www.osfantasticosnumerosprimos.com.br | ||||
| Quadrado Mágico 4x4 | |||||
| 34 | |||||
| 16 | 2 | 3 | 13 | 34 | |
| 5 | 11 | 10 | 8 | 34 | |
| 9 | 7 | 6 | 12 | 34 | |
| 4 | 14 | 15 | 1 | 34 | |
| 34 | 34 | 34 | 34 | 34 | |
| www.osfantasticosnumerosprimos.com.br | |||||
O Quadrado Mágico 4x4 convertido em raízes digitais não forma constante mágica.
O dígito 2 aparece repetido na coluna 2.
Os dígitos equidistantes não formam pares complementares.
| Quadrado Mágico 4x4 | |||||
| convertido em raízes digitais | |||||
| 15 | |||||
| 7 | 2 | 3 | 4 | 16 | |
| 5 | 2 | 1 | 8 | 16 | |
| 9 | 6 | 7 | 3 | 25 | |
| 4 | 5 | 6 | 1 | 16 | |
| 25 | 15 | 17 | 16 | 17 | |
| www.osfantasticosnumerosprimos.com.br | |||||
| Quadrado Mágico 5x5 | ||||||
| 65 | ||||||
| 11 | 4 | 17 | 10 | 23 | 65 | |
| 24 | 12 | 5 | 18 | 6 | 65 | |
| 7 | 25 | 13 | 1 | 19 | 65 | |
| 20 | 8 | 21 | 14 | 2 | 65 | |
| 3 | 16 | 9 | 22 | 15 | 65 | |
| 65 | 65 | 65 | 65 | 65 | 65 | |
| www.osfantasticosnumerosprimos.com.br | ||||||
O Quadrado Mágico 5x5 convertido em raízes digitais não forma constante mágica.
Aparecem dígitos repetidos em linhas e colunas.
Os dígitos equidistantes nas verticais não formam pares complementares.
| Quadrado Mágico 5x5 | ||||||
| convertido em raízes digitais | ||||||
| 29 | ||||||
| 2 | 4 | 8 | 1 | 5 | 0 | 20 |
| 6 | 3 | 5 | 9 | 6 | 29 | |
| 7 | 7 | 4 | 1 | 1 | 20 | |
| 2 | 8 | 3 | 5 | 2 | 20 | |
| 3 | 7 | 9 | 4 | 6 | 29 | |
| 0 | ||||||
| 20 | 29 | 29 | 20 | 20 | 20 | |
| www.osfantasticosnumerosprimos.com.br | ||||||
| Quadrado Mágico 6x6 | |||||||
| 111 | |||||||
| 32 | 29 | 4 | 1 | 24 | 21 | 111 | |
| 30 | 31 | 2 | 3 | 22 | 23 | 111 | |
| 12 | 9 | 17 | 20 | 28 | 25 | 111 | |
| 10 | 11 | 18 | 19 | 26 | 27 | 111 | |
| 13 | 16 | 36 | 33 | 5 | 8 | 111 | |
| 14 | 15 | 34 | 35 | 6 | 7 | 111 | |
| 111 | 111 | 111 | 111 | 111 | 111 | 111 | |
| www.osfantasticosnumerosprimos.com.br | |||||||
O Quadrado Mágico 6x6 convertido em raízes digitais não forma constante mágica.
Aparecem dígitos repetidos em linhas e colunas.
Os dígitos equidistantes não formam pares complementares.
| Quadrado Mágico 6x6 | |||||||
| convertido em raízes digitais | |||||||
| 30 | |||||||
| 5 | 2 | 4 | 1 | 6 | 3 | 21 | |
| 3 | 4 | 2 | 3 | 4 | 5 | 21 | |
| 3 | 9 | 8 | 2 | 1 | 7 | 30 | |
| 1 | 2 | 9 | 1 | 7 | 9 | 29 | |
| 4 | 7 | 9 | 6 | 5 | 8 | 39 | |
| 5 | 6 | 7 | 8 | 6 | 7 | 39 | |
| 21 | 30 | 39 | 21 | 29 | 39 | 30 | |
| www.osfantasticosnumerosprimos.com.br | |||||||
| Quadrado Mágico 7x7 | ||||||||
| 175 | ||||||||
| 22 | 5 | 30 | 13 | 38 | 21 | 46 | 175 | |
| 47 | 23 | 6 | 31 | 14 | 39 | 15 | 175 | |
| 16 | 48 | 24 | 7 | 32 | 8 | 40 | 175 | |
| 41 | 17 | 49 | 25 | 1 | 33 | 9 | 175 | |
| 10 | 42 | 18 | 43 | 26 | 2 | 34 | 175 | |
| 35 | 11 | 36 | 19 | 44 | 27 | 3 | 175 | |
| 4 | 29 | 12 | 37 | 20 | 45 | 28 | 175 | |
| 175 | 175 | 175 | 175 | 175 | 175 | 175 | 175 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||
O Quadrado Mágico 7x7 convertido em raízes digitais não forma constante mágica.
Aparecem dígitos repetidos em linhas e colunas.
Os dígitos equidistantes não formam pares complementares.
| Quadrado Mágico 7x7 | ||||||||
| convertido em raízes digitais | ||||||||
| 33 | ||||||||
| 4 | 5 | 3 | 4 | 2 | 3 | 1 | 22 | |
| 2 | 5 | 6 | 4 | 5 | 3 | 6 | 31 | |
| 7 | 3 | 6 | 7 | 5 | 8 | 4 | 40 | |
| 5 | 8 | 4 | 7 | 1 | 6 | 9 | 40 | |
| 1 | 6 | 9 | 7 | 8 | 2 | 7 | 40 | |
| 8 | 2 | 9 | 1 | 8 | 9 | 3 | 40 | |
| 4 | 2 | 3 | 1 | 2 | 9 | 1 | 22 | |
| 31 | 31 | 40 | 31 | 31 | 40 | 31 | 40 | |
| www.osfantasticosnumerosprimos.com.br | ||||||||
Não se pode afirmar com certeza se o Quadrado Mágico 9x9 convertido em raízes digitais é o único exemplo até o presente momento, mas pode-se afirmar com certeza que nem todos os quadrados mágicos são possíveis de conversões em raízes digitais perfeitas e formarem simetrias, termos complementares e constantes mágicas.
Autor: Ricardo Silva - abril/2024
BALL, W. W. Rouse. Mathematical Recreations and Essays. Release Date: October 8, 2008 [EBook #26839]
Project Gutenberg
DANIELSSON, Holger. Magic Squares. Version 2.12 (date: 05. Mar 2022)
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://mestredoconhecimento.forumeiros.com
https://www.magic-squares.info
https://pt.wikipedia.org
Matemática Básica com Prof Alberto
https://www.youtube.com/watch?v=eSXF0ezqIqM
Matemática Rio com Prof. Rafael Procopio
https://www.youtube.com/watch?v=N-kvzyuSaAU

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato