


A imagem a seguir é um detalhe da Tabela de Divisores publicada na Wikipedia, a qual apresenta um fato matemático interessante: a soma dos divisores próprios de 120 é o seu dobro e a soma de todos os seus divisores é seu o triplo.
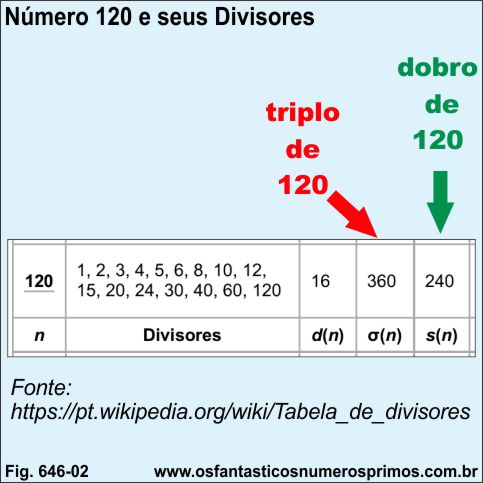
Número Perfeito é um número cuja soma de seus divisores próprios, exceto o próprio número, tem como resultado esse número.
Números Perfeitos estão estritamente relacionados à potências de base 2.
Euclides de Alexandria enuncia em Os Elementos no livro IX:
“Se tantos números quantos quisermos, começando com a unidade, forem colocados continuamente em dupla proporção até que a soma de todos seja um número primo, e se a soma for multiplicada pelo último, então o produto será um número perfeito”.
A fórmula algébrica desta proposição é:
| 2n−1 ( 2n −1 ) |
Euclides faz referências às somas de potências de base 2.
Exemplos:
a) 1 + 2 = 3 ( número primo )
2 x 3 = 6 (número perfeito)
b) 1 + 2 + 4 = 7 ( número primo )
4 x 7 = 28 (número perfeito)
c) 1 + 2 + 4 + 8 + 16 = 31 ( número primo )
16 x 31 = 496 (número perfeito)

D(12) : {1, 2, 3, 4, 5, 6 , 8, 10, 12, 15, 20, 24, 30, 40, 60, 240 }
16 divisores
Fatores primos: 2 x 2 x 2 x 3 x 5
23 x 3 x 5 = 8 x 3 x 5 = 120
8 x 15 = 120
120 produto de um cubo por 2 números primos distintos.
A soma dos divisores próprios de 120 é seu dobro.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 = 240
A soma de todos os divisores de 120 é seu triplo
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Aqui, um fato matemático interessante, a soma dos divisores próprios de 120 é o seu dobro e a soma de todos os seus divisores é seu o triplo.
Tem-se aqui, um novo tipo de número, isto é, um número semelhante a número perfeito.
Se o quociente entre um quadrado perfeito e a metade de sua raiz quadrada for o dobro da raiz quadrada e 2/3 da soma de todos os divisores, então essa raiz é um número semelhante a um número perfeito.
1202 : 60 =
= 14400 : 60 = 240
240 é o dobro de 210
240 é 2/3 de 360
Fatores primos de 120:
i) 2 x 2 x 2 x 3 x 5
ii) 8 x 3 x 5
Troque 8 por 15,
troque 3 por 4,
troque 5 por 6 e os mutipliquem:
15 x 4 x 6 = 360
360 é a soma de todos os divisores de 120.
360 - 120 = 240
240 é a soma de todos os divisores próprios de 120.
240 é o dobro de 120.
240 é 2/3 de 360.
360 é o triplo de 120.
Número quadrado perfeito dividido pela metade de sua raiz quadrada for número divisível pela soma de todos os divisores, bem como, pela a soma dos divisores próprios dessa raiz quadrada, então essa raiz quadrada, pode ser:
a) um número perfeito;
b) ou número semelhante a um número perfeito.
Autor: Ricardo Silva - fevereiro/2026
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/wiki/Tabela_de_divisores

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato