


Vários são os padrões e sequências que podem ser observados na natureza, como intervalo entre dia e noite de 12 horas, 7 dias da semana, 12 meses do ano, 4 fases da Lua, 4 estações do ano, movimentos como de rotação e translação do Sol, etc.
Uma sequência numérica a qual todos lidamos diariamente é a Sequência do Números Naturais, pois, precisamos realizar contagens, fazer operações aritméticas de adição, subtração, multiplicação e divisão; ordenar coisas e objetos; utilizar como códigos em documentos; fazer medições, etc.
Operações aritméticas, dependendo do problema, podem ser feitas, às vezes até mentalmente, em outras situações necessitamos de papel e lápis para se fazer contas, ou ainda fazer uso de calculadoras, planilhas digitais, computadores, etc.
Sendo o problema "complexo" precisamos ainda fazer uso de fórmula matemática.
Uma dessas fórmulas, é a Fórmula Quadrática, Fórmula Resolutiva de Equação do Segundo Grau, também conhecida por nós brasileiros por Fórmula de Bháskara, aliás, há vários outros métodos que foram desenvolvidos para se solucionar problemas do segundo grau.
Veja a relação dos métodos abaixo.
Solucionar problema do segundo grau é encontrar dois números cuja soma e o produto são dados, isto é, encontrar as raízes desses dois números.
Partindo-se desta informação veremos que duplas de números que são raízes formam padrões e sequências numéricas e que nos auxiliam a desvendar alguns "segredos" de Equações do Segundo Grau.
A tabela seguir apresenta duplas de números consecutivos cuja diferença é de 1 unidade, a soma e produto entre eles.
Montando e resolvendo Equações do Segundo Grau com a soma e produto desses pares de números consecutivos, etapas de resolução da equação apresentam os seguintes padrões:
a) a raiz quadrada do segundo membro da equação é 1;
b) 1 é a diferença entre os números consecutivos;
c) a diferença entre os números é que determina o número quadrado do segundo membro da equação;
d) etapas da equação tornam-se frações, pelo fato do termo "bx" ser número ímpar;
| Pares de Números | ||||
| Diferença | soma | produto | ||
| 1 | 1 | 2 | 3 | 2 |
| 2 | 1 | 3 | 5 | 6 |
| 3 | 1 | 4 | 7 | 12 |
| 4 | 1 | 5 | 9 | 20 |
| 5 | 1 | 6 | 11 | 30 |
| www.osfantasticosnumerosprimos.com.br | ||||
O Método de Completar Quadrados para resolver Equações do Segundo Grau consiste em formar um trinômio quadrado perfeito no primeiro membro da equação.
soma: 3 e produto: 2
Monta-se a Equação do Segundo Grau na forma completa.
x2 - 3x + 2 = 0
Completando quadrado
Deloca-se o termo independente "c" 2 para o segundo membro da equação trocando o sinal para -2.
x2 - 3x = - 2
Dividi-se o coeficiente 3 do termo "bx" por 2 (3/2) e eleve ao quadrado (9/4) e some-o ao primeiro e segundo membros para equilibrar a equação.
| 32 | 32 | ||||||||
| x2 | - | 3x | + | ____ | = | - | 2 | + | ___ |
| 22 | 22 |
| 9 | 9 | ||||||||
| x2 | - | 3x | + | ____ | = | - | 2 | + | ___ |
| 4 | 4 |
Efetua-se o Mínimo Múltiplo Comum para se obter frações equivalentes...
| x2 | 3x | 9 | 2 | 9 | |||||
| ____ | - | ____ | + | ____ | = | - | ____ | + | ___ |
| 4 | 4 | 4 | 4 | 4 |
...e consequentemente também uma nova equação equivalente.
4x2 - 12x + 9 = - 8 + 9
O Primeiro membro torna-se um Trinômio Quadrado Perfeito.
Fatora-se o primeiro membro, obtendo-se quadrado da soma (produto notável).
(2x - 3)2 = 1
Extrai-se a raiz quadrada dos dois membros.
2x - 3 = ± √1
2x - 3 = ± 1
As raízes da equação são os números escolhidos da tabela.
| + 1 + 3 | 4 | |||||
| x' | = | ______ | = | ___ | = | 2 |
| 2 | 2 |
| - 1 + 3 | 2 | |||||
| x' | = | ______ | = | ___ | = | 1 |
| 2 | 2 |
soma: 5 e produto: 6
x2 - 5x + 6 = 0
x2 - 5x = - 6
completando o quadrado
x2 - 5x + (5/2)2 = - 6 + (5/2)2
x2 - 5x + (25/4)2 = - 6 + (25/4)2
trinômio quadrado perfeito no primeiro membro
4x2 - 20x + 25 = - 24 + 25
4x2 - 20x + 25 = + 1
(2x - 5)2 = 1
2x - 5 = ± √1
2x - 5 = ± 1
As raízes da equação são os números escolhidos da tabela, cuja soma e produto são dados.
| + 1 + 5 | 6 | |||||
| x' | = | ______ | = | ___ | = | 3 |
| 2 | 2 |
| - 1 + 5 | 4 | |||||
| x' | = | ______ | = | ___ | = | 2 |
| 2 | 2 |
soma: 7 e produto: 12
x2 - 7x + 12 = 0
x2 - 7x = - 12
completando o quadrado
x2 - 7x + (7/2)2 = - 48 + (7/2)2
efetua-se o mmc
x2 - 7x + (49/4)2 = - 48 + (49/4)2
trinômio quadrado perfeito no primeiro membro
4x2 - 28x + 49 = - 48 + 49
4x2 - 28x + 49 = + 1
(2x - 7)2 = 1
2x - 7 = ± √1
2x - 7 = ± 1
As raízes da equação são os números escolhidos da tabela, cuja soma e produto são dados.
| + 1+ 7 | 8 | |||||
| x' | = | ______ | = | ___ | = | 4 |
| 2 | 2 |
| - 1 + 7 | 6 | |||||
| x' | = | ______ | = | ___ | = | 3 |
| 2 | 2 |
soma: 9 e produto: 20
x2 - 9x + 20 = 0
x2 - 9x = - 20
completando o quadrado
x2 - 9x + (9/2)2 = - 20 + (9/2)2
efetua-se o mmc
x2 - 9x + (81/4)2 = - 20 + (81/4)2
trinômio quadrado perfeito no primeiro membro
4x2 - 36x + 81 = - 80 + 81
4x2 - 36x + 81 = + 1
(2x - 9)2 = 1
2x - 9 = ± √1
2x - 9 = ± 1
As raízes da equação são os números escolhidos da tabela, cuja soma e produto são dados.
| + 1 + 9 | 10 | |||||
| x' | = | ______ | = | ___ | = | 5 |
| 2 | 2 |
| - 1 + 9 | 8 | |||||
| x' | = | ______ | = | ___ | = | 4 |
| 2 | 2 |
Formando Equações do Segundo Grau com sequências de duplas de números não consecutivos com diferenças constantes ou não, as resoluções das equações nos exemplos demostrados apresentam regularidades numéricas quanto as raízes quadradas.
A tabela seguir apresenta duplas de números, cuja diferença é um número natural crescente, a soma e produto entre eles.
A diferença entre as duplas de números são as raízes quadradas nas resoluções das equações.
| Pares de Números | ||||
| Diferença | soma | produto | ||
| 1 | 1 | 2 | 3 | 2 |
| 1 | 2 | 3 | 4 | 3 |
| 1 | 3 | 4 | 5 | 4 |
| 1 | 4 | 5 | 6 | 5 |
| 1 | 5 | 6 | 7 | 6 |
| www.osfantasticosnumerosprimos.com.br | ||||
soma: 4 e produto: 3
x2 - 4x + 3 = 0
x2 - 4x = -3
completando o quadrado
x2 - 4x + 22 = - 3 + 22
trinômio quadrado perfeito no primeiro membro
x2 - 4x + 4 = - 3 + 4
(x - 2)2 = 1
x - 2 = ± √1
x - 2 = ± 1
raízes da equação
x' = + 2 + 1 = 3
x" = + 2 - 1 = 1
soma: 5 e produto: 4
x2 - 5x + 4 = 0
x2 - 5x = - 4
completando o quadrado
x2 - 5x + (5/2)2 = - 4 + (5/2)2
efetua-se o mmc
x2 - 5x + (25/4)2 = - 4 + (25/4)2
4x2 - 20x + 25 = - 16 + 25
trinômio quadrado perfeito no primeiro membro
4x2 - 20x + 25 = + 9
(2x - 5)2 = 9
2x - 5 = ± √9
2x - 5 = ± 3
As raízes da equação são os números escolhidos da tabela, cuja soma e produto são dados.
| + 5 + 3 | 8 | |||||
| x' | = | ______ | = | ___ | = | 4 |
| 2 | 2 |
| + 5 - 3 | 2 | |||||
| x' | = | ______ | = | ___ | = | 1 |
| 2 | 2 |
soma: 6 e produto: 5
x2 - 6x + 5 = 0
x2 - 6x = -5
completando o quadrado
x2 - 6x + 32 = - 5 + 32
trinômio quadrado perfeito no primeiro membro
x2 - 6x + 9 = - 5 + 9
(x - 3)2 = 4
x - 3 = ± √4
x - 3 = ± 2
raízes da equação
x' = + 3 + 2 = 5
x" = + 3 - 2 = 1
A tabela seguir apresenta duplas de números, cuja diferença é de 2 unidades, a soma e produto entre eles.
Sendo a diferença entre as duplas de números de 2 unidades, as raízes quadradas nas resoluções das equações é 1.
| Pares de Números | ||||
| Diferença | soma | produto | ||
| 1 | 2 | 3 | 4 | 3 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 2 | 5 | 8 | 15 |
| 4 | 2 | 6 | 10 | 24 |
| 5 | 2 | 7 | 12 | 35 |
| www.osfantasticosnumerosprimos.com.br | ||||
soma: 6 e produto: 8
x2 - 6x + 8 = 0
x2 - 6x = - 8
completando o quadrado
x2 - 6x + 32 = - 8 + 32
trinômio quadrado perfeito no primeiro membro
x2 - 6x + 9 = - 8 + 9
(x - 3)2 = 1
x - 3 = ± √1
x - 3 = ± 1
raízes da equação
x' = + 3 + 1 = 4
x" = + 3 - 1 = 2
soma: 10 e produto: 24
x2 - 10x + 24 = 0
x2 - 10x = - 24
completando o quadrado
x2 - 10x + 52 = - 24 + 22
trinômio quadrado perfeito no primeiro membro
x2 - 10x + 25 = - 24 + 25
(x - 5)2 = 1
x - 5 = ± √1
x - 5 = ±1
raízes da equação
x' = + 5 + 1 = 6
x" = + 5 - 1 = 4
soma: 8 e produto: 15
x2 - 8x + 15 = 0
x2 - 8x = - 15
completando o quadrado
x2 - 8x + 42 = - 15 + 42
trinômio quadrado perfeito no primeiro membro
x2 - 8x + 16 = - 15 + 16
(x - 4)2 = 1
x - 4 = ± √1
x - 4 = ± 1
raízes da equação
x' = + 4 + 1 = 5
x" = + 4 - 1 = 3
A tabela seguir apresenta duplas de números, cuja diferença é de 4 unidades, a soma e produto entre eles.
Sendo a diferença entre as duplas de números de 4 unidades, as raízes quadradas nas resoluções das equações é 2.
| Pares de Números | ||||
| Diferença | soma | produto | ||
| 1 | 4 | 5 | 6 | 5 |
| 2 | 4 | 6 | 8 | 12 |
| 3 | 4 | 7 | 10 | 21 |
| 4 | 4 | 8 | 12 | 32 |
| 5 | 4 | 9 | 14 | 45 |
| www.osfantasticosnumerosprimos.com.br | ||||
soma: 6 e produto: 5
x2 - 6x + 5 = 0
x2 - 6x = - 5
completando o quadrado
x2 - 6x + 32 = - 5 + 32
trinômio quadrado perfeito no primeiro membro
x2 - 6x + 9 = - 5 + 9
(x - 3)2 = 4
x - 3 = ± √4
x - 3 = ± 2
raízes da equação
x' = + 3 + 2 = 5
x" = + 3 - 2 = 1
soma: 8 e produto: 12
x2 - 8x + 12 = 0
x2 - 8x = - 12
completando o quadrado
x2 - 8x + 42 = - 12 + 42
trinômio quadrado perfeito no primeiro membro
x2 - 8x + 16 = - 12 + 16
(x - 4)2 = 4
x - 4 = ± √4
x - 4 = ± 2
raízes da equação
x' = + 4 + 2 = 6
x" = + 4 - 2 = 2
A tabela seguir apresenta duplas de números, cuja diferença é de 3 unidades, a soma e produto entre eles.
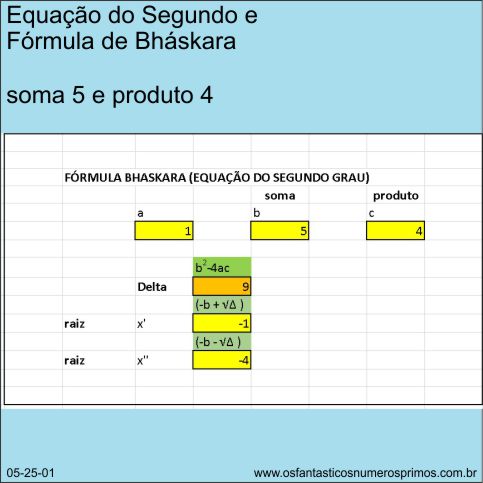
Utilizando a Fórmula Resolutiva de Equação do Segundo Grau (Fórmula de Bháska) em planilha digital com a soma e produto dos pares de números da tabela, as etapas de resolução da equação apresentam os seguintes regularidades:
a) o Delta da equação é 9 - quadrado de 3;
b) 3 é a diferença entre os termos - 3 é raiz quadrada de 9;
c) a diferença entre as duplas de números da tabela é que determina o número quadrado do Delta nas equações.
| Pares de Números | ||||
| Diferença | soma | produto | ||
| 1 | 3 | 4 | 5 | 4 |
| 2 | 3 | 5 | 7 | 10 |
| 3 | 3 | 6 | 9 | 18 |
| 4 | 3 | 7 | 11 | 28 |
| www.osfantasticosnumerosprimos.com.br | ||||
soma: 5 e produto: 4
A diferença dos números números (1 e 4) é a raiz do Δ = 9 na equação.
soma: 7 e produto: 10
A diferença entre os números (2 e 5) é a raiz do Δ = 9 na equação.

soma: 9 e produto: 18
A diferença entre os números (3 e 6) é a raiz do Δ = 9 da equação.

Método de Resolução Convencional
Método da Semi-Soma e do Produto
Método Alternativo
Demonstração Independente do Conhecimento da Fórmula
Resolutiva
Método do Quadrado e da Diferença
Método de Viéte
Método da Substituição De Variáveis
Método de Euler
Método Diferencial ou das Coodernadas do Vértice
Método Fan-Fan ou Método de Horner
Método da Transformação
Métodos Gráficos
Método Gráfico de um Sistema de Equações
Método Cartesiano
Método de Descartes
Métodos Geométricos de Euclides
Método Geometrico Baseado no de Euclides
Método Geométrico de Completar Quadrado
Método Geometrico de Completar o Quadrado alternativo
Outro Método Geométrico
Método da Falsa Posição Dupla
Autor: Ricardo Silva - maio/2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
SAUTOY, Marcus Du. Filme The Story of Maths - The Language of The Universe. The Open University - BBC - XXVIII.
VALE, Alberton Fagno Albino do. As diferentes Estratégias de Resolução da Equação do Segundo Grau. Dissertação apresentada à Universidade Federal Rural do Semiárido – Ufersa, Mossoró, 2013

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato