


Triângulo Aritmético, também conhecido como Triângulo de Pascal, Triângulo de Tartaglia, Triângulo de Yang Hui, etc., é um dispositivo numérico triangular que possui diversas propriedades matemáticas relacionadas a números naturais, números figurados, números primos, números binomiais, números combinatórios, geometria, entre outros.
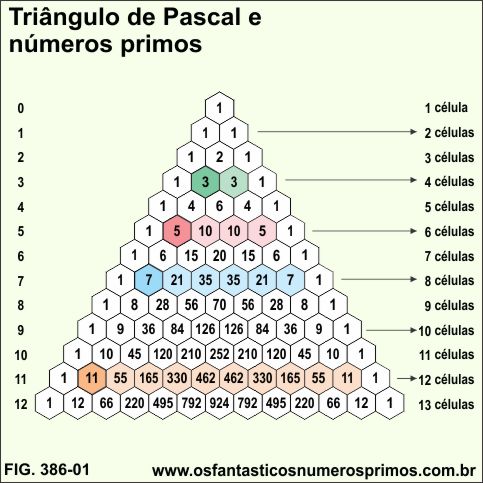
Entre várias regularidades no Triângulo de Pascal, uma delas é que nas linhas em que aparecem números primos, os números entre os números primos são múltiplos desses mesmos números primos, excetuando-se os números primos 2 e 3, pois não há números múltiplos entre o 2 na linha 2 e o 3 na linha 3.
Excetuando-se a linha 0 (zero) que possui uma célula, as demais linhas no Triângulo de Pascal têm quantidades de células 1 unidade maior que a ordem / posição da própria linha.
Determinadas linhas em que há ocorrências de números números primos apresentam também relações numéricas com potências de base 2.
O número primo 5 se encontra na linha 5 no Triângulo de Pascal.
6 são as quantidades de células (termos) na linha 5.
2 são as quantidades de múltiplos entre os números primos 5, na linha 5.
4 subtraído de 6 ou 3 subtraído de 5 tem como resultado 2 que são as quantidades de termos entre os números primos 5.
2 = 21
2 é uma potência de base 2.
O número primo 7 se encontra na linha 7 no Triângulo de Pascal.
8 são as quantidades de células (termos) na linha 7.
4 são as quantidades de múltiplos entre os números primos 7, na linha 7.
4 subtraído de 8 ou 3 subtraído de 7 tem como resultado 4 que são as quantidades de termos entre os números primos 7.
4 = 22
4 é uma potência de base 2.
O número primo 11 se encontra na linha 11 no Triângulo de Pascal.
12 são as quantidades de células (termos) na linha 11.
8 são as quantidades de múltiplos entre os números primos 11, na linha 11.
4 subtraído de 12 ou 3 subtraído de 11 tem como resultado 8 que são as quantidades de termos entre os números primos 11.
8 = 23
8 é uma potência de base 2.
O número primo 19 se encontra na linha 19 no Triângulo de Pascal.
20 são as quantidades de células (termos) na linha 19.
16 são as quantidades de múltiplos entre os números primos 19, na linha 19.
4 subtraído de 20 ou 3 subtraído de 19 tem como resultado 16 que são as quantidades de termos entre os números primos 19.
16 = 24
16 é uma potência de base 2.
O número primo 67 se encontra na linha 67 no Triângulo de Pascal.
68 são as quantidades de células (termos) na linha 67.
64 são as quantidades de múltiplos entre os números primos 67, na linha 67.
4 subtraído de 68 ou 3 subtraído de 67 tem como resultado 64 que são as quantidades de termos entre os números primos 67.
64 = 26
64 é uma potência de base 2.
O número primo 131 se encontra na linha 131 no Triângulo de Pascal.
132 são as quantidades de células (termos) na linha 67.
128 são as quantidades de múltiplos entre os números primos 67, na linha 67.
4 subtraído de 132 ou 3 subtraído de 131 tem como resultado 128 que são as quantidades de termos entre os números primos 131.
128 = 27
128 é uma potência de base 2.
O número primo 4099 se encontra na linha 4099 no Triângulo de Pascal.
4100 são as quantidades de células (termos) na linha 4099.
4096 são as quantidades de múltiplos entre os números primos 4099, na linha 4099.
4 subtraído de 4100 ou 3 subtraído de 4099 tem como resultado 4096 que são as quantidades de termos entre os números primos 4099.
4096 = 212
4096 é uma potência de base 2.
Tabulando-se os dados numéricos em relação às potências de base 2 com números primos no Triângulo de Pascal observa-se:
a) que determinadas potências de base 2 somadas de 3 unidades têm como resultados números primos;
b) que há tanto expoentes ímpares quanto expoentes pares elevados a base 2;
c) que as ocorrências de números primos são aleatórias.
| Potências de base 2 | ||||||
|---|---|---|---|---|---|---|
| somadas de 3 unidades | ||||||
| base 2 | expoente | potência | soma | primo | ||
| de base 2 | ||||||
| 2 | 0 | 1 | + | 3 | 4 | |
| 2 | 1 | 2 | + | 3 | 5 | sim |
| 2 | 2 | 4 | + | 3 | 7 | sim |
| 2 | 3 | 8 | + | 3 | 11 | sim |
| 2 | 4 | 16 | + | 3 | 19 | sim |
| 2 | 5 | 32 | + | 3 | 35 | |
| 2 | 6 | 64 | + | 3 | 67 | sim |
| 2 | 7 | 128 | + | 3 | 131 | sim |
| 2 | 8 | 256 | + | 3 | 259 | |
| 2 | 9 | 512 | + | 3 | 515 | |
| 2 | 10 | 1024 | + | 3 | 1027 | |
| 2 | 11 | 2048 | + | 3 | 2051 | |
| 2 | 12 | 4096 | + | 3 | 4099 | sim |
| 2 | 13 | 8192 | + | 3 | 8195 | |
| 2 | 14 | 16384 | + | 3 | 16387 | |
| 2 | 15 | 32768 | + | 3 | 32771 | sim |
| 2 | 16 | 65536 | + | 3 | 65539 | sim |
| 2 | 17 | 131072 | + | 3 | 131075 | |
| 2 | 18 | 262144 | + | 3 | 262147 | sim |
| 2 | 19 | 524288 | + | 3 | 524291 | |
| 2 | 20 | 1048576 | + | 3 | 1048579 | |
| 2 | 21 | 2097152 | + | 3 | 2097155 | |
| 2 | 22 | 4194304 | + | 3 | 4194307 | |
| 2 | 23 | 8388608 | + | 3 | 8388611 | |
| 2 | 24 | 16777216 | + | 3 | 16777219 | |
| 2 | 25 | 33554432 | + | 3 | 33554435 | |
| 2 | 26 | 67108864 | + | 3 | 67108867 | |
| 2 | 27 | 134217728 | + | 3 | 134217731 | |
| 2 | 28 | 268435456 | + | 3 | 268435459 | sim |
| 2 | 29 | 536870912 | + | 3 | 536870915 | |
| 2 | 30 | 1073741824 | + | 3 | 1073741827 | sim |
| 2 | 31 | 2147483648 | + | 3 | 2147483651 | |
| 2 | 32 | 4294967296 | + | 3 | 4294967299 | |
| 2 | 33 | 8589934592 | + | 3 | 8589934595 | |
| 2 | 34 | 17179869184 | + | 3 | 17179869187 | |
| 2 | 35 | 34359738368 | + | 3 | 34359738371 | |
| 2 | 36 | 68719476736 | + | 3 | 68719476739 | |
| www.osfantasticosnumerosprimos.com.br | ||||||
Assim como os números primos, determinados números compostos, apresentam em suas respectivas linhas números múltiplos deles próprios.
O número composto 9 é um número múltiplo e também quadrado de 3.
Dividindo os números que aparecem na linha 9 por 9 têm-se que nem todos os quocientes são números inteiros:
| Triângulo de Pascal | ||||
| múltiplos de 9 | ||||
| divididos por 9 | ||||
| 9 | : | 9 | = | 1 |
| 36 | : | 9 | = | 4 |
| 84 | : | 9 | = | 9,333... |
| 126 | : | 9 | = | 14 |
| 126 | : | 9 | = | 14 |
| 84 | : | 9 | = | 9,333... |
| 36 | : | 9 | = | 4 |
| 9 | : | 9 | = | 1 |
| www.osfantasticosnumerosprimos.com.br | ||||
O número composto 25 é um número múltiplo e também quadrado de 5.
Dividindo os números que aparecem na linha 25 do Triângulo de Pascal por 25 têm-se que nem todos os quocientes são números inteiros:
| Triângulo de Pascal | ||||
| múltiplos de 25 | ||||
| divididos por 25 | ||||
| 25 | : | 25 | = | 1 |
| 300 | : | 25 | = | 12 |
| 2300 | : | 25 | = | 92 |
| 12650 | : | 25 | = | 506 |
| 53130 | : | 25 | = | 2125,2 |
| 177100 | : | 25 | = | 7084 |
| 480700 | : | 25 | = | 19228 |
| 1081575 | : | 25 | = | 43263 |
| 2042975 | : | 25 | = | 81719 |
| 3268760 | : | 25 | = | 130750,4 |
| 4457400 | : | 25 | = | 178296 |
| 5200300 | : | 25 | = | 208012 |
| 5200300 | : | 25 | = | 208012 |
| 4457400 | : | 25 | = | 178296 |
| 3268760 | : | 25 | = | 130750,4 |
| 2042975 | : | 25 | = | 81719 |
| 1081575 | : | 25 | = | 43263 |
| 480700 | : | 25 | = | 19228 |
| 177100 | : | 25 | = | 7084 |
| 53130 | : | 25 | = | 2125,2 |
| 12650 | : | 25 | = | 506 |
| 2300 | : | 25 | = | 92 |
| 300 | : | 25 | = | 12 |
| 25 | : | 25 | = | 1 |
| www.osfantasticosnumerosprimos.com.br | ||||
O número composto 49 é um número múltiplo e também quadrado de 7.
Dividindo os números que aparecem na linha 49 do Triângulo de Pascal por 49 têm-se que nem todos os quocientes são números inteiros:
| Triângulo de Pascal | ||||
| múltiplos de 49 | ||||
| divididos por 49 | ||||
| 49 | : | 49 | = | 1 |
| 1176 | : | 49 | = | 24 |
| 18424 | : | 49 | = | 376 |
| 211876 | : | 49 | = | 4324 |
| 1906884 | : | 49 | = | 38916 |
| 13983816 | : | 49 | = | 285384 |
| 85900584 | : | 49 | = | 1753073,143 |
| 450978066 | : | 49 | = | 9203634 |
| 2054455634 | : | 49 | = | 41927666 |
| 8217822536 | : | 49 | = | 167710664 |
| 29135916264 | : | 49 | = | 594610536 |
| 92263734836 | : | 49 | = | 1882933364 |
| 2,62597E+11 | : | 49 | = | 5359118036 |
| 6,75249E+11 | 49 | = | 13780589235 | |
| 1,57558E+12 | 49 | = | 32154708216 | |
| 3,34811E+12 | 49 | = | 68328754959 | |
| 6,49927E+12 | 49 | = | 1,32638E+11 | |
| 1,15543E+13 | 49 | = | 2,35801E+11 | |
| 1,88517E+13 | 49 | = | 3,84728E+11 | |
| 2,82775E+13 | 49 | = | 5,77092E+11 | |
| 3,90499E+13 | 49 | = | 7,96937E+11 | |
| 4,96999E+13 | 49 | = | 1,01428E+12 | |
| 5,83434E+13 | 49 | = | 1,19068E+12 | |
| 6,32053E+13 | 49 | = | 1,2899E+12 | |
| 6,32053E+13 | 49 | = | 1,2899E+12 | |
| 5,83434E+13 | 49 | = | 1,19068E+12 | |
| 4,96999E+13 | 49 | = | 1,01428E+12 | |
| 3,90499E+13 | 49 | = | 7,96937E+11 | |
| 2,82775E+13 | 49 | = | 5,77092E+11 | |
| 1,88517E+13 | 49 | = | 3,84728E+11 | |
| 1,15543E+13 | 49 | = | 2,35801E+11 | |
| 6,49927E+12 | 49 | = | 1,32638E+11 | |
| 3,34811E+12 | 49 | = | 68328754959 | |
| 1,57558E+12 | 49 | = | 32154708216 | |
| 6,75249E+11 | 49 | = | 13780589235 | |
| 2,62597E+11 | 49 | = | 5359118036 | |
| 92263734836 | 49 | = | 1882933364 | |
| 29135916264 | 49 | = | 594610536 | |
| 8217822536 | 49 | = | 167710664 | |
| 2054455634 | 49 | = | 41927666 | |
| 450978066 | 49 | = | 9203634 | |
| 85900584 | 49 | = | 1753073,143 | |
| 13983816 | 49 | = | 285384 | |
| 1906884 | 49 | = | 38916 | |
| 211876 | 49 | = | 4324 | |
| 18424 | 49 | = | 376 | |
| 1176 | 49 | = | 24 | |
| 49 | 49 | = | 1 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Autor: Ricardo Silva - maio /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato