


Número palíndromo ou número capicua é um número que pode ser lido tanto da esquerda para à direita quanto da direita para à esquerda e o seu valor continua sendo o mesmo.
Exemplos:
11
121
808
A cada sequência de dez números consecutivos, tem-se um número palíndromo.
10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
Há números palíndromos / capicuas que são formados pela repetição de um mesmo algarismo e esse mesmo algarismo pode estar em quantidades ímpares ou pares.
Exemplos:
11
111
1111
11111
Há números palíndromos / capicuas que são formados por combinações de algarismos distintos cujos algarismos ou os conjuntos dos mesmos algarismos são os que dividem simetricamente o número.
Exemplos:
121
131
1221
1331
Números binários são números formados por dois algarismos: o zero (0) e o um (1) e que são utilizados em sistemas digitais como em computadores para codificar algarismos, letras, cores, sons e caracteres especiais.
Os algarismos 0 e 1 são denominados de bit (binary digit) e o conjunto de 8 bits formam o byte (Binary term).
Na tabela a seguir, têm-se as representações em números binários os 20 primeiros números naturais / decimais.
| Tabela de correspondência | |
|---|---|
| de números binários | |
| e números decimais | |
| Binário | Decimal |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| www.osfantasticosnumerosprimos.com.br | |
Determinados números naturais / decimais quando convertidos em números binários também formam palíndromos / capicuas constituídos de um só algarismo binário...
Exemplos:
3 em binário = 11
7 em binário = 111
15 em binário = 1111
e outros com a combinação dos dois algarismos binários.
exemplos:
5 em binário = 101
9 em binário = 1001
17 em binário = 10001
A partir de 1 e dobrando-se os valores, obtêm-se potências de base 2 ou elevando o número 2 a expoentes sucessivos.
Potências de base 2 quando convertidas em números binários, o primeiro bit é sempre o bit 1. O bit 1 neste caso funciona como um "identificador" de potências de base 2 em números binários.
Outra regularidade é que a base 2 elevada a determinado expoente é o que determina também a quantidade de bits zeros (0) e consequentemente as potências de 10.
Observação: há uma relação direta entre o número 2 e suas potências, pois o 2 é divisor das potências e as potências são divisíveis por 2.
| Tabela 2 | ||
|---|---|---|
| Correspondência | ||
| de potências de base 2 | ||
| e números binários | ||
| N | Decimal | Binário |
| 2N | ||
| 0 | 1 | 1 |
| 1 | 2 | 10 |
| 2 | 4 | 100 |
| 3 | 8 | 1000 |
| 4 | 16 | 10000 |
| 5 | 32 | 100000 |
| 6 | 64 | 1000000 |
| 7 | 128 | 10000000 |
| 8 | 256 | 100000000 |
| 9 | 512 | 1000000000 |
| 10 | 1.024 | 10000000000 |
| 11 | 2.048 | 100000000000 |
| 12 | 4.096 | 1000000000000 |
| 13 | 8.192 | 10000000000000 |
| 14 | 16.384 | 100000000000000 |
| 15 | 32.768 | 1000000000000000 |
| 16 | 65.536 | 10000000000000000 |
| 17 | 131.072 | 100000000000000000 |
| 18 | 262.144 | 1000000000000000000 |
| 19 | 524.288 | 10000000000000000000 |
O número 3 multiplicado por potências de base 2 e posteriormente convertidos em números binários, apresentam como identificador binário os bits: 11.
A quantidade de bit 0, aumenta conforme o expoente a partir da 1ª ordem.
Cada múltiplo de 3 é o dobro do anterior a partir do próprio número 3.
Observação: há uma relação direta entre o número 3 e os produtos, pois o 3 é divisor dos produtos e os produtos são divisíveis por 3.
| Produtos de 3 por uma potência de base 2 convertidos em número binário |
||||||
|---|---|---|---|---|---|---|
| Ordem | Número | Potência de 2 | Produto | Binário | ||
| 0ª | 3 | 20 | = | 1 | 3 | 11 |
| 1ª | 3 | 21 | = | 2 | 6 | 110 |
| 2ª | 3 | 22 | = | 4 | 12 | 1100 |
| 3ª | 3 | 23 | = | 8 | 24 | 11000 |
| 4ª | 3 | 24 | = | 16 | 48 | 110000 |
| 5ª | 3 | 25 | = | 32 | 96 | 1100000 |
| 6ª | 3 | 26 | = | 64 | 192 | 11000000 |
| 7ª | 3 | 27 | = | 128 | 384 | 110000000 |
| 8ª | 3 | 28 | = | 256 | 768 | 1100000000 |
| www.osfantasticosnumerosprimos.com.br | ||||||
As potências de base 3 convertidas em números binários não apresentam identificador binário comum.
Observação: há uma relação direta entre a base 3 e suas potências, pois o 3 é divisor das potências e as potências são divisíveis por 3.
| Correspondência | ||
|---|---|---|
| de potências de base 3 | ||
| e números binários | ||
| N | Decimal | Binário |
| 3N | ||
| 0 | 1 | 1 |
| 1 | 3 | 11 |
| 2 | 9 | 1001 |
| 3 | 27 | 11011 |
| 4 | 81 | 1010001 |
| 5 | 243 | 11110011 |
| 6 | 729 | 1011011001 |
| 7 | 2187 | 100010001011 |
O número 5 multiplicado por potências de base 2 e posteriormente convertidas em números binários, apresentam como identificador binário os bits: 101.
Observação: há uma relação direta entre o número 5 e os produtos, pois o 5 é divisor dos produtos e os produtos são divisíveis por 5.
| Produtos de 5 por uma potência de base 2 convertidos em número binário |
||||||
|---|---|---|---|---|---|---|
| Ordem | Número | Potência de 2 | Produto | Binário | ||
| 0ª | 5 | 20 | = | 1 | 5 | 101 |
| 1ª | 5 | 21 | = | 2 | 10 | 1010 |
| 2ª | 5 | 22 | = | 4 | 20 | 10100 |
| 3ª | 5 | 23 | = | 8 | 40 | 101000 |
| 4ª | 5 | 24 | = | 16 | 80 | 1010000 |
| 5ª | 5 | 25 | = | 32 | 160 | 10100000 |
| 6ª | 5 | 26 | = | 64 | 320 | 101000000 |
| 7ª | 5 | 27 | = | 128 | 640 | 1010000000 |
| 8ª | 5 | 28 | = | 256 | 1280 | 10100000000 |
| www.osfantasticosnumerosprimos.com.br | ||||||
As potências de base 5 convertidas em números binários não apresentam identificador binário comum.
Observação: há uma relação direta entre a base 5 e suas potências, pois o 5 é divisor das potências e as potências são divisíveis por 5.
| Correspondência | ||
|---|---|---|
| de potências de base 5 | ||
| e números binários | ||
| N | Decimal | Binário |
| 5N | ||
| 0 | 1 | 1 |
| 1 | 5 | 101 |
| 2 | 25 | 11001 |
| 3 | 125 | 1111101 |
| 4 | 625 | 1001110001 |
| 5 | 3125 | 110000110101 |
| 6 | 15625 | 11110100001001 |
| 7 | 78125 | 10011000100101101 |
Número perfeito é um número cuja soma dos seus divisores, excluindo o próprio número, tem como resultado o próprio número.
Sequência dos 10 primeiros números perfeitos
01) 6
02) 28
03) 496
04) 8.128
05) 33.550.336
06) 8.589.869.056
07) 137.438.691.328
08) 2.305.843.008.139.952.128
09)2.658
10)191.561
Alguns números perfeitos, seus divisores e suas somas.
D(6): 1, 2, 3, 6
A soma dos divisores excluído o próprio número:
1 + 2 + 3 = 6
D(28): 1, 2, 4, 7, 14, 28
A soma dos divisores excluído o próprio número:
1 + 2 + 4 + 7 + 14 = 28
D(496): 1, 2, 4, 8, 16, 31, 62, 124, 248, 496
A soma dos divisores excluído o próprio número:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
D(8128): 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064, 8128
A soma dos divisores excluído o próprio número:
1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128
D(33.550.336): 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8191, 16382, 32764, 131056, 262112, 524224, 1048448, 2096896, 4193792, 8387584, 16775168, 33550336
A soma dos divisores excluído o próprio número:
1 + 2 + 4 + 8 + 16 + 32 + 64... + 8387584 +16775168 + 33550336 = 33.550.336
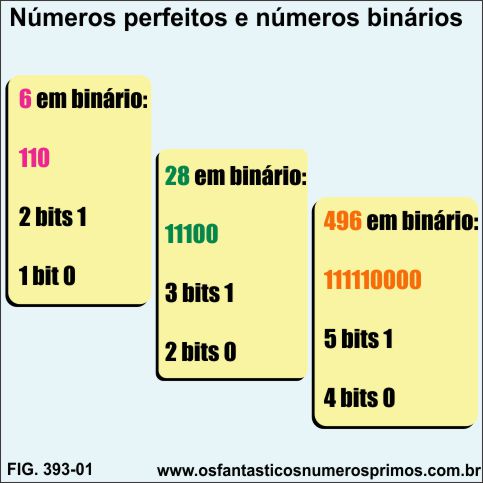
Número perfeito não é múltiplo e nem divisor de um outro número perfeito, mas convertidos em números binários apresentam um padrão numérico em suas formações binárias:
a) os bits 1 são em quantidades de números primos;
b) os bits 0 são em quantidades 1 unidade menor que os bits 1.
Interessante observar que suas formações binárias são assimétricas e não formam palíndromos / capicuas.
Quanto a soma dos conjuntos de bits de cada número perfeito convertidos em binários, há somas que têm como resultados números primos e outras números quadrados perfeitos.
110
2 bits 1
1 bit 0
soma dos bits = 3
11100
3 bits 1
2 bits 0
soma dos bits = 5
111110000
5 bits 1
4 bits 0
soma dos bits = 9
1111111000000
7 bits 1
6 bits 0
soma dos bits = 13
1111111111111000000000000
13 bits 1
12 bits 0
soma dos bits = 25
111111111111111110000000000000000
17 bits 1
16 bits 0
soma dos bits = 33
1111111111111111111000000000000000000
19 bits 1
18 bits 0
soma dos bits = 37
1111111111111111111111111111111
31 bits 1
30 bits 0
Observação importante: na verificação e confirmação de números binários, utilizou-se o WebSite Império do Números.
Autor: Ricardo Silva - junho/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato