Página de estudos de matemática e sequências numéricas

Palíndromos e o produto de um número pelo seu inverso- 163

Números palíndromos ou capicuas são números que podem ser lidos em ordem inversa, isto é, tanto da esquerda para a direita quanto da direita para a esquerda.

O método tradicional de se obter um número palíndromo é escolher um número qualquer, inverter os seus algarismos e depois somá-los com este número.

Nem sempre este método resulta em um número palíndromo, então tem que se repetir o processo várias vezes e mesmo repetindo talvez não se consiga formar um palíndromo, é o caso do número 196.

Mas não é garantido que todos os números não palindrômicos irão gerar um palíndromo desta maneira. Embora isto não seja provado, muitos números não conseguem gerar um palíndromo desta maneira. Por exemplo, o número 196 não consegue gerar um palíndromo mesmo depois de 700.000.000 de iterações. Qualquer número que nunca gerar um palíndromo desta maneira é chamado de números de Lychrel.[1]

Produto de um número com a inversão de seus algarismos

Outro método de se obter números palíndromos ou capicua é multiplicar um número pelo inversão de seus algarismos, conforme veremos, também não é possível gerar palíndromos constantemente.

O interessante neste método é que a diferença entre um palíndromo e outro palíndromo; ou um palíndromo e um não-palíndromo pode ter como resultado um número palíndromo.

O número 11 é o primeiro número primo palíndromo de dois algarismos e ele é obtido da seguinte forma:

10 + 01 = 11

Interessante também é que o produto de 11 por ele mesmo ou elevado ao quadrado tem como resultado o primeiro número palíndromo de 3 algarismos gerado por meio de multiplicação.

11 x 11 = 121

11² = 121

Semelhante a simetria do número palíndromo 121, há outros produtos que são gerados por números em que o algarismo 1 se repete, tanto no número gerador quanto no número gerado.

111² = 12321

1111² = 1234321

11111² = 123454321

Formando palíndromos através de multiplicação

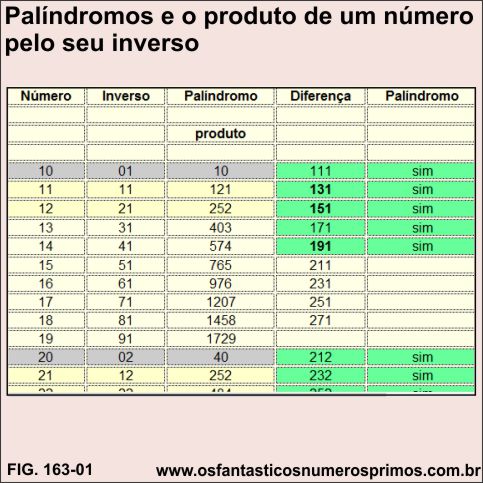
A tabela apresenta a sequência dos números de 10 a 102 com a inversão de seus algarismos, os quais foram multiplicados e cujos produtos estão na coluna Palíndromo (Produto).

Em um estudo com os 1000 primeiros naturais, os números que geraram palíndromos por meio de multiplicação têm finais 1 e 2 (células amarela).

Observação: a geração de palíndromos por meio de multiplicação não é constante em toda a tabela.

A diferença entre um produto anterior por produto posterior de números pelos seus inversos geram sequências de palíndromos.

Exemplos)

121 - 10 = 111

252 - 121 = 131

403 - 252 = 151

A cada sequência de 10 números, a diferença entre produtos geram 5 números palíndromos e esta ocorrência é constante em toda a tabela com os 1000 primeiros números naturais.

Na coluna Diferença (células verde) os números palíndromos podem ser gerados:

a) pela diferença entre um palíndromo e outro palíndromo;

b) pela diferença entre um palíndromo e não-palíndromo;

c) pela diferença entre um não-palíndromo e não-palíndromo.

Na mesma coluna Diferença há ocorrências de números primos palíndromos: 131, 151, 191, 313, 353, 373, 757, 797, 919, 10301, 10501.

Os números palíndromos e os números primos palíndromos gerados através desde método apresentam como padrão o seu termo central um número ímpar.

Números primos palíndromos

Num rol de 1000 números foram gerados 52 números primos palíndromos.

Abaixo está a sequência dos 46 primeiros números palíndromos publicada na página do Wikipédia - Número primo palíndromo.

Os números que estão destacados, são os números que também foram gerados por meio do método descrito neste estudo.

Foi possível gerar todos os números primos palíndromos cujos termos centrais são números ímpares divulgados no Wikipédia.

Os demais números primos palíndromos foram divididos simultaneamente por alguns números primos para se verificar se eram múltiplos.

Houve mais uma verificação por meio da lista publicada no site The Prime Page

Autor: Ricardo Silva - janeiro/2018

Fonte bibliográfica:

[1] Sena , Hugo Tácito Azevedo de . Algumas evidências computacionais da infinitude dos números primos palindrômicos e generalizações destes. Monografia. Universidade Federal do Rio Grande do Norte,2008.

Matérias relacionadas:

011-estudos-125-numero-trinta-e-sete-regularidades-numericas

011-estudos-138-numeros-primos-numeros-binarios

011-estudos-159-numeros-naturais-e-inversao-seus-algarismos

011-estudos-160-numeros-primos-numeros-capicuas

011-estudos-161-numeros-primos-numeros-palindromos

011-estudos-162-numeros-palindromos

011-estudos-163-palindromos-produto-numero-seu-inverso

011-estudos-219-o-enigmatico-numero-196

011-estudos-163-palindromos-produto-numero-seu-inverso

011-estudos-250-numero-capicua

L A N Ç A M E N T O ! ! !

NOVO LIVRO DIGITAL:

DESCOBRINDO NÚMEROS PRIMOS A PARTIR DE NÚMEROS COMPOSTOS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.