


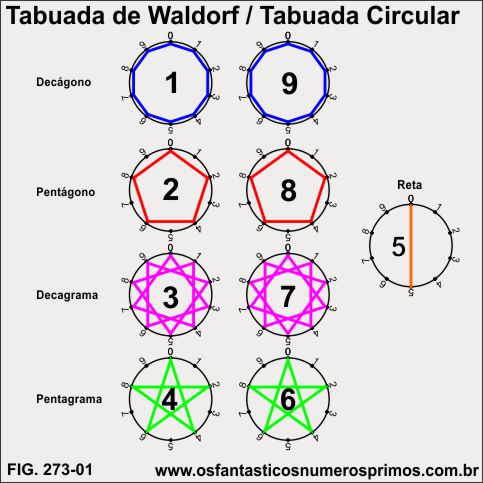
Tabuada de Waldorf, também conhecida como Tabuada Circular são circunferências divididas em dez 10 partes iguais e numeradas de 0 a 9 nas quais são marcadas os múltiplos dos números de 1 a 9 em cada uma das circunferências a partir dos algarismos finais desses múltiplos.
Interessante nestes modelos de tabuadas de multiplicações é que formam duplas de figuras geométricas simétricas, excetuando-se a tabuada do 5.
As duplas de figuras geométricas também apresentam padrões entre elas em relações a números ímpares e pares.
O 1 e o 9 formam um decágono - polígono com 10 lados.
O 3 e o 7 formam um decagrama - estrela com 10 pontas.
O 2 e o 8 formam um pentàgono - polígono de 5 lados.
O 4 e o 6 forma um pentagrama - estrela de 5 pontas.
Para montar as tabuadas seguem-se os seguintes passos:
Em sentido horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 1, começando no ponto 1 e no final aparecerá figura de um decágono.
1, 2, 3, 4, 5, 6, 7, 8 e 9.
Em sentido anti-horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 9, começando no ponto 9 e no final aparecerá figura de um decágono.
1, 2, 3, 4, 5, 6, 7, 8 e 9.
Em sentido horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 2, começando no ponto 2 e no final aparecerá figura de um pentágono.
2, 4, 6, 8, 0, 2, 4, 6, 8, 0.
Em sentido anti-horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 8, começando no ponto 8 e no final aparecerá figura de um pentágono.
8, 6, 4, 2, 0, 8, 6, 4, 2, 8.
Em sentido horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 3, começando no ponto 3 e no final aparecerá figura de um decagrama que é uma estrela de 10 pontas.
3, 6, 9, 2, 5, 8, 1, 4, 7, 0.
Em sentido anti-horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 7, começando no ponto 7 e no final aparecerá figura de um decagrama que é uma estrela de 10 pontas.
7, 4, 1, 8, 5, 2, 9, 6, 3, 0.
Em sentido horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 4, começando no ponto 4 e no final aparecerá figura de um pentagrama que é uma estrela de 5 pontas.
4, 8, 2, 6, 0, 4, 8, 2, 6, 0.
Em sentido anti-horário, desenham-se seguimentos de retas a partir dos algarismos finais dos múltiplo de 6, começando no ponto 6 e no final aparecerá figura de um pentagrama que é uma estrela de 5 pontas.
6, 2, 8, 4, 0, 6, 2, 8, 4, 0.
Tabuada de Multiplicação conhecida também por Tabuada de Pitágoras, Tabuada Pitagórica ou Tabuada Cartesiana é um dispositivo numérico com a sequência dos números de 1 a 10 na linha e coluna principal em que na intersecção de dois números obtem-se produtos entre eles.
A sua principal propriedade é que de uma forma sintética tem-se os múltiplos dos números de 1 a 10, bem como, seus respectivos produtos.
A Tabuada de Pitágoras possui diversas outras propriedades aritméticas, algébricas e numéricas embutidas em sua contrução e que estão publicados no livro digital Tabuada de Pitágoras e Sequências Numéricas que inclusive apresenta um nova sequência numérica formada por potências em que as bases e expoentes são números ímpares consecutivos: 3 1 , 5 3 , 7 5, 9 7 , 11 9...
| Tabuada de Pitágoras | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |||||||||
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |||||||||
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |||||||||
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||||||||
Os algarismos finais de múltiplos ímpares apresentam simetrias entre eles e podemos melhor analisá-los na presente tabela:
a) os algarismos nos extremos, excluindo o 0 (zero), em diagonais, são os mesmos;
b) a soma de dois termos equidistantes, tanto horizontal e verticamente, tem como resultado 10;
c) o número 5, excluindo o 0 (zero), é o termo médio de cada sequência, bem como a média aritmética da soma de números de termos equidistantes;
| Algarismos finais | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| de múltiplos ímpares | ||||||||||
| números | algarismos finais | |||||||||
| ímpares | ||||||||||
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 3 | 3 | 6 | 9 | 2 | 5 | 8 | 1 | 4 | 7 | 0 |
| 7 | 7 | 4 | 1 | 8 | 5 | 2 | 9 | 6 | 3 | 0 |
| 9 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
Os algarismos finais de múltiplos pares apresentam simetrias entre eles e podemos melhor analisá-los na presente tabela:
a) os algarismos nos extremos, excluindo o 0 (zero) da última coluna à direita, em diagonais são os mesmos;
b) o número 0, excluindo o 0 (zero) da última coluna à direita, é o que divide cada sequência;
c) a soma de dois termos equidistante, tanto horizontal e verticamente, tem como resultado 10;
| Algarismos finais | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| de múltiplos pares | ||||||||||
| números | algarismos finais | |||||||||
| pares | ||||||||||
| 2 | 2 | 4 | 6 | 8 | 0 | 2 | 4 | 6 | 8 | 0 |
| 4 | 4 | 8 | 2 | 6 | 0 | 4 | 8 | 2 | 6 | 0 |
| 6 | 6 | 2 | 8 | 4 | 0 | 6 | 2 | 8 | 4 | 0 |
| 8 | 8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 | 0 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
Autor: Ricardo Silva - setembro /2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato