


O presente estudo demonstra regularidades numéricas quando se multiplica o número 9 por número natural.
Os produtos apresentam em suas formações, às vezes, o próprio algarismo 9 e sequências de algarismos que quando somados tem como resultado também 9 e seus múltiplos.
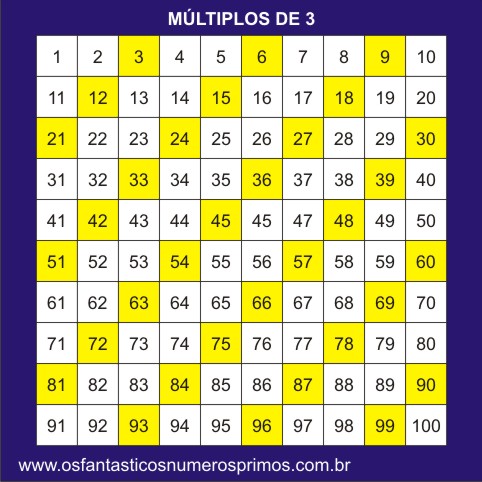
Na sequência dos números naturais, a cada três números, há um múltiplo de 3.
Todos os múltiplos de 9 são múltiplos de 3, mas nem todo múltiplo de 3 é múltiplo de 9.
Escolhendo-se qualquer múltiplo de 3 e somando-se sempre 9 unidades, os números resultantes tendem a formar uma linha diagonal.
3, 12 e 21.
6, 15, 24, 33, 42 e 51.
9, 18, 27, 36, 45, 54, 63, 72 e 81.
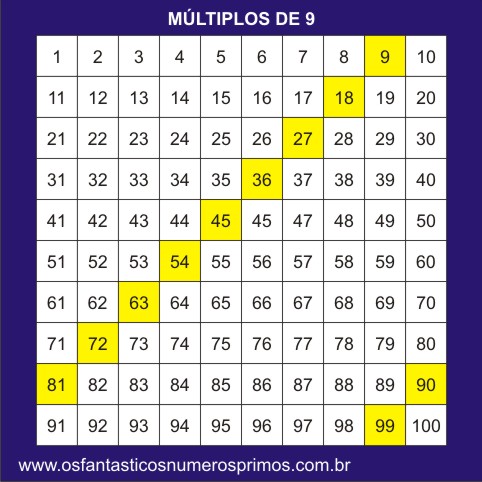
Na sequência dos números naturais, a cada nove números, há um múltiplo de 9.
Todos os múltiplos de 9 são múltiplos de 3.
Escolhendo-se qualquer múltiplo de 9 e somando-se sempre nove unidades, os números resultantes tendem a formar uma linha diagonal.
9, 18, 27, 36, ...
90, 99, ...
Os números 3 e 9 apresentam algumas propriedades em comum:
a) os números aparecem em linhas diagonais quando inscritos em diagramas como mostrados acima;
b) multiplos de 9 também são múltiplos de 3;
c) as somas dos algarismos dos múltiplos são múltiplos de 3
O número 9 tem uma interessante particularidade: a soma de dois algarismos de seus primeiros múltiplos tem como resultado o próprio número 9 a partir do múltiplo 18 até o múltiplo 90.
A soma dos algarismos dos produtos acontecem sequencialmente e tem como resultado o número 9;
A soma dos algarimos dos múltiplos de 9 são números múltiplos e divisíveis tanto por 9 quanto por 3.
9 x 1= 9
9 x 2 = 18 (1 + 8 = 9)
9 x 3 = 27 (2 + 7 = 9)
9 x 4 = 36 (3 + 6 = 9)
9 x 5 = 45 (4 +5 = 9)
9 x 6 = 54 (5+ 4 = 9)
9 x 7 = 63 (6 + 3 + 9)
9 x 8 = 72 (7 + 2 = 9)
9 x 10 = 90 ( 9 + 0 = 9)
11 x 9 = 99 (9 + 9 = 18)
12 x 9 = 108 (1 + 0 + 8 = 9)
20 x 9 = 180 ( 1 + 8 + 0 = 9)
21 x 9 = 189 ( 1 + 8 + 9 = 18)
30 x 9 = 270 ( 2 + 7 + 0 = 9)
31 x 9 = 279 ( 2 + 7 + 9 = 18)
Quando um dos fatores da multiplicação for um número cujo o algarismo 1 se repete, o produto será um número baseado em tantas vezes que o algarismo 1 se repete.
Exemplo 1)
1 x 9 = 9
11 x 9 = 99
111 x 9 = 999
Quando um dos fatores da multiplicação for um número diferente de 1 e cujo o algarismo se repete, o produto será determinado conforme especificações a seguir:
Exemplo 2)
2 x 9 = 18
22 x 9 = 198
No número 22, o algarismo 2 repete duas vezes; os algarismos do número 18 se encontra nos extremos do número 198; é como se estivéssemos escrevendo o número 198 com dois números 9 da seguinte forma: um 9 desmembrado em (1 e 8 nos extremos) e o outro 9 no meio do número 198.
Exemplo 3)
222 x 9 = 1998
No número 222, o algarismo 2 repete três vezes; os algarismos do número 18 se encontra nos extremos do número 1998; é como se estivéssemos escrevendo o número 1998 com três números 9 da seguinte forma: um 9 desmembrado em (1 e 8 nos extremos) e os outros dois 9 no meio do número 1998.
Exemplo 4)
3 x 9 = 27
33 x 9 = 297
333 x 9 = 2997
Exemplo 5)
4 x 9 = 36
44 x 9 = 396
444 x 9 = 3996
Exemplo 6)
5 x 9 = 45
55 x 9 = 495
555 x 9 = 4995
Exemplo 7)
6 x 9 = 54
66 x 9 = 594
666 x 9 = 5994
Exemplo 8)
7 x 9 = 63
77 x 9 = 693
777 x 9 = 6993
Exemplo 9)
8 x 9 = 72
88 x 9 = 792
888 x 9 = 7992
Exemplo 10)
9 x 9 = 81
99 x 9 = 891
999 x 9 = 8991
Quando um dos fatores da multiplicação for um número terminado em 0 (zero):
Exemplo 11)
10 x 9 = 90
1010 x 9 = 9090
101010 x 9 = 909090
20 x 9 = 180
2020 x 9 = 18180
202020 x 9 = 1818180
30 x 9 = 270
3030 x 9 = 27270
303030 x 9 = 2727270
40 x 9 = 360
4040 x 9 = 36360
404040 x 9 = 3636360
Quando um dos fatores da multiplicação for um número número cujos algarismos se repetem de forma alternada:
Exemplo 12)
A multiplicação: 2 x 9 = 18, o número 18 aparece separados por seus algarismos nos extremos dos produtos a seguir:
12 x 9 = 108
1212 x 9 = 10908
121212 x 9 = 1090908
Exemplo 13)
A multiplicação: 3 x 9 = 27, somando-se 1 + 1 = 2 e juntando 2 e 7, temos 27.
13 x 9 = 117
1313 x 9 = 11817
131313 x 9 = 1181817
Exemplo 14)
A multiplicação: 4 x 9 = 36, somando-se 1 + 2 = 3 e juntando 3 e 6, temos 36.
14 x 9 = 126
1414 x 9 = 12726
141414 x 9 = 1272726
Exemplo 15)
A multiplicação: 5 x 9 = 45, somando-se 1 + 3 = 4 e juntando 4 e 5, temos 45.
15 x 9 = 135
1515 x 9 = 13635
151515 x 9 = 1363635
Número quadrado perfeito cuja soma dos algarismos é um múltiplo de 9, quando dividido por 9 tem como quociente um outro número quadrado perfeito.
soma dos algarismos 3 + 6 = 9
36 : 9 = 4
4 é um número quadrado perfeito
soma dos algarismos 8 + 1 = 9
81 : 9 = 9
9 é um número quadrado perfeito
soma dos algarismos 1 + 4 + 4 = 9
144 : 9 = 16
16 é um número quadrado perfeito
soma dos algarismos 2 + 2 + 5 = 9
225 : 9 = 25
25 é um número quadrado perfeito
Autor: Ricardo Silva - dezembro/2015
O Web-Site Os Fantásticos Números Primos lança um desafio a você estimado visitante: de construir um triângulo pitagórico inscrito numa circunferência somente com régua não graduada e compasso semelhante ao triângulo retângulo de 30, 60 e 90 graus para ser publicado na Seção Texto do WebSite.
Enviando o seu estudo e modelo matemático da sua solução, para o nosso e:mail:
contato@osfantasticos
você receberá como cortesia:
O livro digital OS FANTÁSTICOS NÚMEROS PRIMOS
Veja as matérias:
005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia
005-texto-018-triangulo-pitagorico3-4-5-inscrito-semicircunferencia
sobre construções de triângulos.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato