


Há um "truque mágico", isto é, uma atividade em Matemática Recreativa, que se faz com a Sequência de Fibonacci em que consiste escolher quaisquer dez termos consecutivos e descobrir a soma desses mesmos dez termos.[1]
Por exemplo, na sequência de 1, 1, ... ,34, 55, qual é a soma?
| Sequência de Fibonacci | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
E o "truque mágico" é multiplicar por 11 o sétimo termo da sequência escolhida.
11 x 13 = 143
1 + 1 + 2 + 5 + 8 + 13 + 21 + 34 + 55 = 143
Outra dica é fazer cálculo mental de 11 multiplicado por um número qualquer, basta repetir o número deslocando para a esquerda e somá-los.
| 1 | 3 | ||
| 1 | 3 | + | |
| 1 | 4 | 3 |
Para mais informações teóricas de como este técnica funciona veja [2].
Obtem-se a Sequência de Fibonacci, repetindo-se o número 1 duas vezes e a partir do terceiro pela soma dos dois números anteriores.
| Sequência de Fibonacci | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
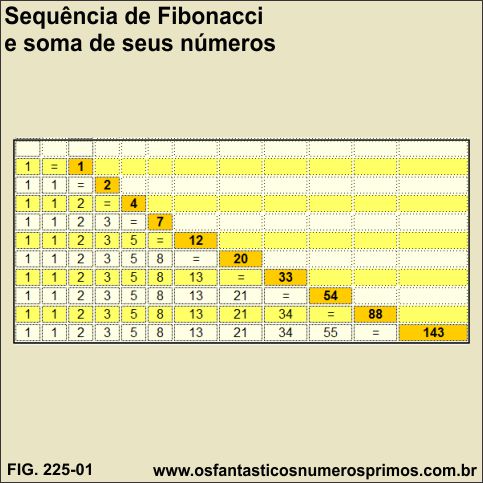
A soma de números concecutivos da Sequência de Fibonacci tem como resultado uma unidade menor do que o segundo termo subsequente.
| Soma | |||||||||||
| de números consecutivos | |||||||||||
| de Fibonacci | |||||||||||
| 1 | = | 1 | |||||||||
| 1 | 1 | = | 2 | ||||||||
| 1 | 1 | 2 | = | 4 | |||||||
| 1 | 1 | 2 | 3 | = | 7 | ||||||
| 1 | 1 | 2 | 3 | 5 | = | 12 | |||||
| 1 | 1 | 2 | 3 | 5 | 8 | = | 20 | ||||
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | = | 33 | |||
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | = | 54 | ||
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | = | 88 | |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | = | 143 |
Exemplos:
1 + 1 = 2
2 é uma unidade menor que 3 ( 40 termo)
1 + 1 + 2 = 4
4 é uma unidade menor que 5 (50 termo)
1 + 1 + 2 + 3 = 7
7 é uma unidade menor que 8 ( 60 termo)
A soma de números de Fibonacci em posições ímpares tem como resultado um número de Fibonacci.
O resultado da soma se encontra na posição posterior ao último termo ímpar da soma.
| Sequência de Fibonacci | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
| Soma de termos | ||||||||||||
| de ordem / posições ímpares | ||||||||||||
| de Fibonacci | ||||||||||||
| 1 | = | 1 | ||||||||||
| 1 | = | |||||||||||
| 1 | + | 2 | = | 3 | ||||||||
| 1 | 2 | = | ||||||||||
| 1 | + | 2 | + | 5 | + | 8 | ||||||
| 1 | 2 | 5 | = | |||||||||
| 1 | + | 2 | + | 5 | + | 13 | + | 21 | ||||
| 1 | 2 | 5 | = | |||||||||
| 1 | + | 2 | + | 5 | + | 13 | + | 34 | + | 55 | ||
| 1 | + | 2 | + | 5 | + | 13 | + | 34 | + | 89 | = | 143 |
Exemplos:
1 + 2 = 3 (3 se encontra na 4a posição)
1 + 2 + 5 = 8 (8 se encontra na 6a posição)
1 + 2 + 5 + 13 = 21 (21 se encontra na 8a posição)
A soma de números de Fibonacci em posições pares tem como resultado uma unidade menor de um número de Fibonacci.
O resultado da soma se encontra na posição posterior ao último termo par da soma.
| Sequência de Fibonacci | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
| Soma de termos | |||||||||||
| de ordem / posições pares | |||||||||||
| de Fibonacci | |||||||||||
| = | |||||||||||
| 1 | 1 | ||||||||||
| 1 | + | 3 | = | 4 | |||||||
| 1 | + | 3 | + | 8 | = | 12 | |||||
| 1 | + | 3 | + | 8 | + | 21 | 33 | ||||
| 1 | + | 3 | + | 8 | + | 21 | + | 55 | = | 88 | |
Exemplos:
1 + 3 = 4 (1 unidade menor de 5 - da 5a posição)
1 + 3 + 8 = 12 (1 unidade menor de 13 - da 7a posição)
1 + 3 + 8 + 21 = 33 (1 unidade menor de 34 - da 9a posição)
| Фn | ||
| F (n) | = | |
| √ 5 | ||
onde:
F(n) = posição / ordem de um termo de Fibonacci
Фn = phi (1,618
√ 5 = 2,236
Exemplo:
Calcular o 120 termo da Sequência de Fibonacci, isto é, F12
| Ф12 | ||
| F (12) | = | ____ |
| √ 5 |
| 1,61803312 | ||
| F (12) | = | _________ |
| 2,2360 |
| 321,9945 | ||
| F (12) | = | _________ |
| 2,2360 |
| F (12) | = | 144,0047 |
O 120 termo da Sequência de Fibonacci é o número 144.
Autor: Ricardo Silva - julho/2019
[1] CARVALHO, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências - São Paulo: Modena, 1997
[2] CORDEIRO, Allison. Tópicos de Aritmética: a sequência de Fibonacci. Departamento de Matemática - UFPR, Curitiba, PR, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato