


Os estudos que se seguem demonstram que por meio de números quadrados perfeitos são possíveis de se determinarem as quantidades de termos dos grupos dos primeiros membros quanto dos segundos membros, obtendo dessa forma sequências infinitas de somas de números triangulares consecutivos, pois o primeiro termo do segundo membro da soma de números triangulares consecutivos é de ordem / posição um número quadrado perfeito.
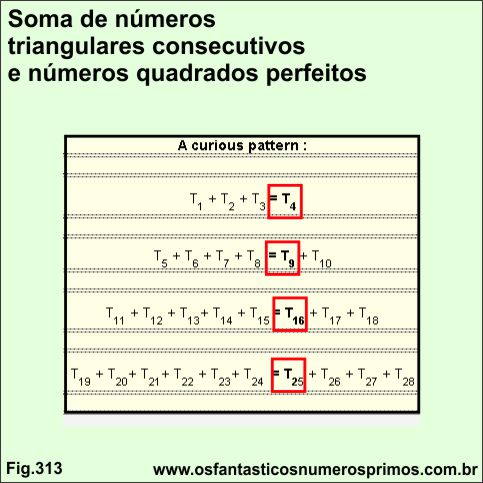
A tabela abaixo apresenta grupos de somas de sequências de números triangulares consecutivos cuja soma do grupo do primeiro membro é igual ao do segundo membro.
Ela está originalmente, até o presente momento, publicada no WebSite:
http://www.shyamsundergupta.com
Título: Curious properties of Triangular Numbers
Item: A curious pattern:
Ela apresenta diversas propriedades algébricas e aritméticas, estudos estes, que estão publicados aqui no WebSite Os Fantásticos Números Primos:
011-estudos-311-soma-numeros-triangulares-consecutivos
Observação: a notação T1 indica:
a) T é a primeira letra da palavra Triangular;
b) 1, 2, 3, 4, 5,... subescrito indica a ordem / posição, isto é, o índice de um número triangular;
c) o primeiro termo do segundo membro tem ordem / posição um número quadrado perfeito.
| A curious pattern : |
| T1 + T2 + T3 = T4 |
| T5 + T6 + T7 + T8 = T9 + T10 |
| T11 + T12 + T13+ T14 + T15 = T16 + T17 + T18 |
| T19 + T20+ T21+ T22 + T23+ T24 = T25 + T26 + T27 + T28 |
O número quadrado perfeito 4 determina 3 números triangulares no primeiro membro e 1 número no segundo membro da soma de números triangulares consecutivos.
Extrai-se a raiz quadrada de 4.
√4 = 2
Subtrai-se 1 unidade da raiz quadrada 2.
2 - 1 = 1
1 é a quantidade de termos do segundo membro.
Soma-se 1 unidade à raiz quadrada 2.
2 + 1 = 3
3 é quantidade de termos do primeiro membro.
| T1 + T2 + T3 = T4 |
1 + 2 + 3 = 10
10 é o triangular de posição/ordem 4.
O número quadrado perfeito 9 determina 2 números triangulares no primeiro membro e 4 números no segundo membro da soma de números triangulares consecutivos.
Extrai-se a raiz quadrada de 9.
√9 = 3
Subtrai-se 1 unidade da raiz quadrada 3.
3 - 1 = 2
2 é a quantidade de termos do segundo membro.
Soma-se 1 unidade à raiz quadrada 3.
3 + 1 = 4
4 é quantidade de termos do primeiro membro.
| T5 + T6 + T7 + T8 = T9 + T10 |
15 + 21 + 28 + 36 = 100
45 + 55 = 100
O número quadrado perfeito 16 determina 3 números triangulares no primeiro membro e 5 números no segundo membro da soma de números triangulares consecutivos.
Extrai-se a raiz quadrada de 16.
√16 = 4
Subtrai-se 1 unidade da raiz quadrada 4.
4 - 1 = 3
3 é a quantidade de termos do segundo membro.
Soma-se 1 unidade à raiz quadrada 4.
4 + 1 = 5
5 é quantidade de termos do primeiro membro.
| T11 + T12 + T13+ T14 + T15 = T16 + T17 + T18 |
66 + 78 + 91+ 105 + 120 = 460
136 + 153 + 171 = 460
O número quadrado perfeito 25 determina 4 números triangulares no primeiro membro e 6 números no segundo membro da soma de números triangulares consecutivos.
Extrai-se a raiz quadrada de 25.
√25 = 4
Subtrai-se 1 unidade da raiz quadrada 5.
5 - 1 = 4
3 é a quantidade de termos do segundo membro.
Soma-se 1 unidade à raiz quadrada 5.
5 + 1 = 6
6 é quantidade de termos do primeiro membro.
| T19 + T20+ T21+ T22 + T23+ T24 = T25 + T26 + T27 + T28 |
190 + 210 + 231+ 253 + 276 + 300 = 1460
325 + 351 + 378 + 406 = 1460
Autor: Ricardo Silva - dezembro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato