


Multiplicando-se um número por ele mesmo obtem-se um outro número o qual denominamos de número quadrado, aliás, um número natural multiplicado por ele mesmo tem como resultado um número quadrado perfeito, porque extraindo-se a sua raiz quadrada, o resultado é esse mesmo número natural.
Todo número natural é a raiz de um outro número, mas nem todo número natural é um número quadrado perfeito, um número cúbico perfeito, um número de quarta, quinta, sexta potência, e assim por diante.
Gerar um número quadrado perfeito é uma tarefa relativamente simples, desde que esse número não tenha várias, várias e várias casas decimais.
Para se saber se determinado número é ou não um número quadrado perfeito (sem uso de dispositivos digitais, como: calculadoras, computadores, etc.) e desde que esse número também não tenha várias e várias casas decimais, pode se fazer o uso do Algoritmo Decomposição de um Número Natural em Fatores Primos, algoritmo este que faz parte do curriculum do 60 ano do ensino fundamental no nosso país.
Exemplo:
Qual é a raiz quadrada de 144?
| Decomposição em fatores primos | |
| número 144 | |
| Fatores Primos | |
| 144 | 2 |
| 72 | 2 |
| 36 | 2 |
| 18 | 2 |
| 9 | 3 |
| 3 | 3 |
| 1 | |
| www.osfantasticosnumerosprimos.com.br | |
√144=
= √2² x 2² x 3²
= 2 x 2 x 3
= 12
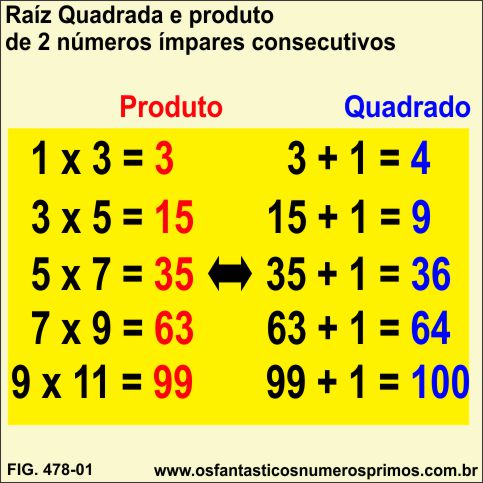
O presente estudo demonstra relações entre números quadrados perfeitos e as somas e produtos de números ímpares consecutivos.
Os produtos de 2 números ímpares consecutivos têm com resultados números que são 1 unidade menor que números quadrados perfeitos pares.
Os produtos de 2 números ímpares consecutivos são números quase quadrados perfeitos.
Exemplos:
a) 3 é 1 unidade menor que o quadrado perfeito 4.
b) 15 é 1 unidade menor que o quadrado perfeito 16.
c) 35 é 1 unidade menor que o quadrado perfeito 36.
Para mais informações, veja abaixo, matérias relacionadas!
| Produtos de 2 | |||||
| números ímpares consecutivos | |||||
| ordem / | multiplicação | produto | |||
| posição | |||||
| 1 | 1 | x | 3 | = | 3 |
| 2 | 3 | x | 5 | = | 15 |
| 3 | 5 | x | 7 | = | 35 |
| 4 | 7 | x | 9 | = | 63 |
| 5 | 9 | x | 11 | = | 99 |
| 6 | 11 | x | 13 | = | 143 |
| 7 | 13 | x | 15 | = | 195 |
| 8 | 15 | x | 17 | = | 255 |
| 9 | 17 | x | 19 | = | 323 |
| 10 | 19 | x | 21 | = | 399 |
| 11 | 21 | x | 23 | = | 483 |
| 12 | 23 | x | 25 | = | 575 |
| 13 | 25 | x | 27 | = | 675 |
| 14 | 27 | x | 29 | = | 783 |
| 15 | 29 | x | 31 | = | 899 |
| 16 | 31 | x | 33 | = | 1023 |
| 17 | 33 | x | 35 | = | 1155 |
| 18 | 35 | x | 37 | = | 1295 |
| 19 | 37 | x | 39 | = | 1443 |
| 20 | 39 | x | 41 | = | 1599 |
| www.osfantasticosnumerosprimos.com.br | |||||
A diferença entre dois números quadrados perfeitos consecutivos tem como resultado um número ímpar.
Exemplos:
a) 4 - 1 = 3
b) 9 - 4 = 5
c) 16 - 9 = 7
Para mais informações, veja abaixo, matérias relacionadas!
| Diferença entre | ||
| 2 números quadrados perfeitos | ||
| Diferença | ||
| de quadrados | ||
| Número | Quadrado | (ímpares) |
| 1 | 1 | |
| 3 | ||
| 2 | 4 | |
| 5 | ||
| 3 | 9 | |
| 7 | ||
| 4 | 16 | |
| 9 | ||
| 5 | 25 | |
| 11 | ||
| 6 | 36 | |
| 13 | ||
| 7 | 49 | |
| 15 | ||
| 8 | 64 | |
| 17 | ||
| 9 | 81 | |
| 19 | ||
| 10 | 100 | |
| 21 | ||
| 11 | 121 | |
| 23 | ||
| 12 | 144 | |
| 25 | ||
| 13 | 169 | |
| 27 | ||
| 14 | 196 | |
| 29 | ||
| 15 | 225 | |
| 31 | ||
| 16 | 256 | |
| 33 | ||
| 17 | 289 | |
| 35 | ||
| 18 | 324 | |
| 37 | ||
| 19 | 361 | |
| 39 | ||
| 20 | 400 | |
| 41 | ||
| 21 | 441 | |
| www.osfantasticosnumerosprimos.com.br | ||
As somas das diferenças de números quadrados perfeitos apresentam as seguintes propriedades:
a) as somas pares são múltiplos de 8;
8, 24, 48, 80,... são múltiplos de 8.
b) as somas pares divididas por 8 têm como resultado números triangulares;
8 : 8 = 1 ( 1 é um número triangular)
24 : 8 = 3 ( 3 é um número triangular)
48 : 8 = 6 ( 6 é um número triangular)
c) as somas pares divididas por 4 têm como resultado números retangulares;
8 : 4 = 2 ( 2 é um número retangular)
24 : 4 = 6 ( 6 é um número retangular)
48 : 4 = 12 ( 6 é um número retangular)
d) as somas ímpares são produtos de 2 números ímpares consecutivos, e entre eles, números primos;
a) 15 = 3 x 5
b) 35 = 5 x 7
c) 63 = 7 x 9
| Soma das diferenças | ||||
| de números quadrados perfeitos | ||||
| somas | ||||
| diferença | diferença | diferenças | ||
| raiz | raiz | quadrado | quadrado | quadrados |
| 1 | 1 | |||
| 1 | 3 | |||
| 2 | 4 | |||
| 1 | 5 | 8 | ||
| 3 | 9 | |||
| 1 | 7 | 15 | ||
| 4 | 16 | |||
| 1 | 9 | 24 | ||
| 5 | 25 | |||
| 1 | 11 | 35 | ||
| 6 | 36 | |||
| 1 | 13 | 48 | ||
| 7 | 49 | |||
| 1 | 15 | 63 | ||
| 8 | 64 | |||
| 1 | 17 | 80 | ||
| 9 | 81 | |||
| 1 | 19 | 99 | ||
| 10 | 100 | |||
| 1 | 21 | 120 | ||
| 11 | 121 | |||
| 1 | 23 | 143 | ||
| 12 | 144 | |||
| 1 | 25 | 168 | ||
| 13 | 169 | |||
| 1 | 27 | 195 | ||
| 14 | 196 | |||
| 1 | 29 | 224 | ||
| 15 | 225 | |||
| 1 | 31 | 255 | ||
| 16 | 256 | |||
| 1 | 33 | 288 | ||
| 17 | 289 | |||
| 1 | 35 | 323 | ||
| 18 | 324 | |||
| 1 | 37 | 360 | ||
| 19 | 361 | |||
| 1 | 39 | 399 | ||
| 20 | 400 | |||
| www.osfantasticosnumerosprimos.com.br | ||||
Partindo-se das relações entre números quadrados perfeitos, produtos de 2 números ímpares consecutivos, diferenças de quadrados e somas das diferenças de quadrados podemos extrair raiz quadrada exata por 3 diferentes métodos, vejamos:
Qual é a raiz quadrada de 4 ?
a) subtrái-se 1 unidade do quadrado perfeito 4;
4 - 1 = 3
Observações importantes:
1 x 3 = 3 ( 3 é produto de 2 ímpares consecutivos)
4 - 1 = 3 ( 3 é diferença entre os quadrados 4 e 1)
3 é a soma das diferenças de quadrados.
b) quais são 2 números ímpares distintos cuja soma é 4 é o produto é 3;
soma
1 + 3 = 4
produto
1 x 3 = 3
Por meio de Equação do Segundo Grau (Método Completando Quadrado), podemos verificar quais são dois números cuja soma e o produto são dados.
Neste caso queremos saber as duas parcelas da soma e os dois fatores do produto.
(i) x . ( x + 2) = 3
(ii) x² + 2x = 3
completando o quadrado
(iii) x² + 2x + 1 = 3 + 1
(iv) ( x + 1 )² = 4
(v) x + 1 = ± √4
(vi) x + 1 = ± 2
(vii) x´ = + 2 - 1 = 1
(viii) x´´= - 2 - 1 = - 3
Verificação
1² + 2.1 = 3
( -3² ) + 2.( -3 ) = 3
c) soma das parcelas dividida por 2
( 1 + 3 ) / 2 = 2
2 é a raíz quadrada de 4
d) soma dos fatores dividida por 2
1 x 3 = 3
(1 + 3) / 2 = 2
2 é a raíz quadrada de 4
Por meio da seguinte fórmula, onde:
Dq = Diferença entre dois quadrados perfeitos
Dr² = Diferença entre duas raízes ao quadrado
2r = Dobro da diferença entre duas raízes
podem ser comprovadas:
a) a raiz quadrada sucessora - Fórmula da Soma
| Dq + Dr² |
| ____ |
| 2 x r |
A diferença das raízes ao quadrado (1²) somada com diferença dos quadrados (3) e dividida pelo dobro da diferença da raízes têm como quociente a √4 = 2.
| 3 + 1² | 4 | |||
| ____ | = | ___ | = | 2 |
| 2 x 1 | 2 |
Para mais informações, veja abaixo, matérias relacionadas!
Qual é a raiz quadrada de 16 ?
a) subtrái-se 1 unidade do quadrado perfeito 16;
16 - 1 = 15
Observações importantes:
3 x 5 = 15 ( 15 é produto de 2 ímpares consecutivos)
16 - 1 = 15 ( 15 é diferença entre os quadrados 16 e 1 )
15 é a soma das diferenças de quadrados.
b) quais são 2 números ímpares distintos cuja soma é 8 é o produto é 15;
soma
3 + 5 = 8
produto
3 x 5 = 15
Por meio de Equação do Segundo Grau (Método Completando Quadrado), podemos verificar quais são dois números cuja soma e o produto são dados.
Neste caso queremos saber as duas parcelas da soma e os dois fatores do produto.
(i) x . ( x + 2) = 15
(ii) x² + 2x = 15
completando o quadrado
(iii) x² + 2x + 1 = 15 + 1
(iv) ( x + 1 )² = 16
(v) x + 1 = ± √16
(vi) x + 1 = ± 4
(vii) x´ = + 4 - 1 = 3
(viii) x´´= - 4 - 1 = - 5
Verificação
3² + 2.3 = 15
( -5² ) + 2.( -5 ) = 15
c) soma das parcelas dividida por 2
( 3 + 5 ) / 2 = 4
4 é a raíz quadrada de 16
d) soma dos fatores dividida por 2
3 x 5 = 8
(3 + 5) / 2 = 4
4 é a raíz quadrada de 16
| Dq + Dr² |
| ____ |
| 2 x r |
A diferença das raízes ao quadrado (3²) somada à diferença dos quadrados (15) e dividida pelo dobro da diferença da raízes têm como quociente a √4 = 2.
| 15 + 3² | 24 | |||
| ____ | = | ___ | = | 4 |
| 2 x 3 | 6 |
Qual é a raiz quadrada de 36 ?
a) subtrái-se 1 unidade do quadrado perfeito 36;
36 - 1 = 35
Observações importantes:
5 x 7 = 35 ( 35 é produto de 2 ímpares consecutivos)
36 - 1 = 35 ( 35 é diferença entre os quadrados 36 e 1 )
35 é a somas das diferenças de quadrados.
b) quais são 2 números ímpares distintos cuja soma é 12 é o produto é 35;
soma
5 + 7 = 12
produto
5 x 7 = 35
Neste caso queremos saber as duas parcelas da soma e os dois fatores do produto.
(i) x . ( x + 2) = 35
(ii) x² + 2x = 35
completando o quadrado
(iii) x² + 2x + 1 = 35 + 1
(iv) ( x + 1 )² = 36
(v) x + 1 = ± √36
(vi) x + 1 = ± 6
(vii) x´ = + 6 - 1 = 5
(viii) x´´= - 6 - 1 = - 7
Verificação
5² + 2.5 = 35
( -4² ) + 2.( -14 ) = 35
c) soma das parcelas dividida por 2
( 5 + 7 ) / 2 = 6
6 é a raíz quadrada de 36
d) soma dos fatores dividida por 2
5 x 7 = 35
(5 + 7) / 2 = 6
6 é a raíz quadrada de 36
Fórmula da Soma
| Dq + Dr² |
| ____ |
| 2 x r |
A diferença das raízes ao quadrado (5²) somada à diferença dos quadrados (35) e dividida pelo dobro da diferença da raízes têm como quociente a √36 = 6.
| 35 + 5² | 60 | |||
| ____ | = | ___ | = | 6 |
| 2 x 5 | 10 |
Qual é a raiz quadrada de 64 ?
a) subtrái-se 1 unidade do quadrado perfeito 64;
64 - 1 = 63
Observações importantes:
7 x 9 = 63 ( 63 é produto de 2 ímpares consecutivos)
64 - 1 = 63 ( 63 é diferença entre os quadrados 64 e 1 )
63 é a somas das diferenças de quadrados.
b) quais são 2 números ímpares distintos cuja soma é 16 é o produto é 63;
soma
7 + 9 = 16
produto
7 x 9 = 63
Neste caso queremos saber as duas parcelas da soma e os dois fatores do produto.
(i) x . ( x + 2) = 63
(ii) x² + 2x = 63
completando o quadrado
(iii) x² + 2x + 1 = 63 + 1
(iv) ( x + 1 )² = 64
(v) x + 1 = ± √64
(vi) x + 1 = ± 8
(vii) x´ = + 8 - 1 = 7
(viii) x´´= - 8 - 1 = - 9
Verificação
7² + 2.7 = 63
( -9² ) + 2.( -9 ) = 63
c) soma das parcelas dividida por 2
( 7 + 9 ) / 2 = 8
8 é a raíz quadrada de 64
d) soma dos fatores dividida por 2
7 x 9 = 63
(7 + 9) / 2 = 8
8 é a raíz quadrada de 64
| Dq + Dr² |
| ____ |
| 2 x r |
A diferença das raízes ao quadrado (7²) somada à diferença dos quadrados (63) e dividida pelo dobro da diferença da raízes têm como quociente a √64 = 6.
| 63 + 7² | 112 | |||
| ____ | = | ___ | = | 8 |
| 2 x 7 | 14 |
Para números quadrados perfeitos ímpares podemos também utilizar a Fórmula Diferença de Quadrados e Diferenças de Raízes.
Para mais informações, veja:
011-estudos-479-raiz-quadrada-produto-dois-numeros-pares-consecutivos.
Autor: Ricardo Silva - dezembro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato